Sedimentation is a simple physical phenomenon in which particles or agglomerates in a solution sediment due to gravity or centrifugal forces. Because this phenomenon is so simple, it is widely used in many technologies, such as toxicology, biochemistry, biomedicine, genetics, and pharmaceutical engineering. In this blog post, we will talk about a mathematical model for how gravity affects sedimentation in test tubes, and how to make a practical app for nanotoxicology (as one example among a variety of applications).

Extracted DNA, in which particles sediment to the bottom of the test tube. Image by Isaevde — Own work. Licensed under CC BY-SA 4.0, via Wikimedia Commons.
How Sedimentation Is Used in Biochemistry
Since March 2020, the spreading COVID-19 pandemic has affected our lives in different ways. You might have taken a polymerase chain reaction (PCR) test, one of the most frequently used technologies for testing for COVID-19, before traveling or at work. Kary Mullis and Michael Smith are recognized as the inventors of the PCR and were awarded the Nobel Prize in 1993 for their invention. Similarly, the pandemic has necessitated COVID-19 vaccines in hope of preventing the spread of the virus. The leading contributors for the technology behind the mRNA-based SARS-CoV-2 vaccines, Drs. Drew Weissman and Katalin Karikó were awarded the 2021 Lasker Award, America’s top biomedical research prize.
Over the course of the pandemic, we have involuntarily heard and seen many genetic engineering terms, such as virus, vaccine, PCR, and mRNA, almost every day. These terms are all made up of, or related to, so-called biomolecules. A variety of biomolecules can be characterized by the sedimentation coefficient in the use of a centrifuge. The pioneer of this study is Swedish chemist Theodor Svedberg, who was awarded the Nobel Prize in 1926 for his studies on disperse systems. His last initial is now the unit name of the sedimentation coefficient (S, svedberg), which represents how quickly the particles reach a terminal velocity under a certain force (gravity or centrifugal force). The full eukaryotic ribosome has a sedimentation coefficient of 80 S, for example.
While it is believed that COVID-19 is a natural disease, there are manmade diseases, such as air pollution, caused by a various size range (from nanometers to microns) of particles (typically metals) emitted from factories, automobiles, and other manmade materials and pollution sources. The field of toxicology studies how these particles are harmful to human health. Dosimetry is one of the key technologies that accounts for the discrepancy between in vivo (animal testing) and in vitro (cell-based assay) results. More accurate quantification and prediction of the dose and concentration of particles is expected to contribute to more accurate in vitro experiments. Sedimentation experiments and simulations are used for that purpose.
In biomedical studies, blood sedimentation is used to study inflammation in the human body. Faster sedimentation means more inflammation as well as an indication of certain diseases that feature the production of abnormal proteins, such as multiple myeloma. Sedimentation is also used to separate white blood cells, red blood cells, and platelets. In pharmaceutical applications, sedimentation is used for drug separation from the mother liquor after crystallization and insulin purification from other protein materials (for example, “A Review on Centrifugation in the Pharmaceutical Industry“). Studies on drug adsorption and desorption are also important for the pharmaceutical industry.
A large number of significantly important applications use sedimentation. Although sedimentation or centrifugation can be relatively easy and quick to experiment with, it is absolutely advantageous to use a computer, which can simulate a number of combinations of materials and conditions at once. In addition, mathematical modeling is often essential to understanding complex sedimentation phenomena, such as adsorption and desorption.
Equations for Sedimentation Using Test Tubes Under Gravity
For bioengineering, genetic engineering, medical engineering, and pharmaceutical applications, ultrahigh-speed centrifuges are used to separate particles or molecules. This is mainly because biomolecules are “stickier” than other types of particles and larger forces are required for sedimentation. (Imagine how sticky biomaterials containing DNAs/RNAs are: The length of 90 times the distance between the Earth and the Sun is entangled and packed in a pair of DNA strands.) You can find commercial centrifuges that can generate as much as 70,000 g (in this case, the unit for gravity). There are types of centrifuges that have a laser source that shines on the horizontally spinning test tube, which makes it possible to measure concentration in real time.
The governing equation for describing sedimentation by centrifuges is called the Lamm equation. Ole Lamm was a PhD student of Svedberg. This equation is simply the cylindrical coordinate version of the Mason–Weaver equation, which we discuss in this blog post.
Compared to biomolecules, particles (typically metals or ceramics) for toxicology studies are much heavier and sink more quickly. So, the gravity does the job for such an application. A test tube is placed vertically and particles sink vertically, as depicted in the following figure.
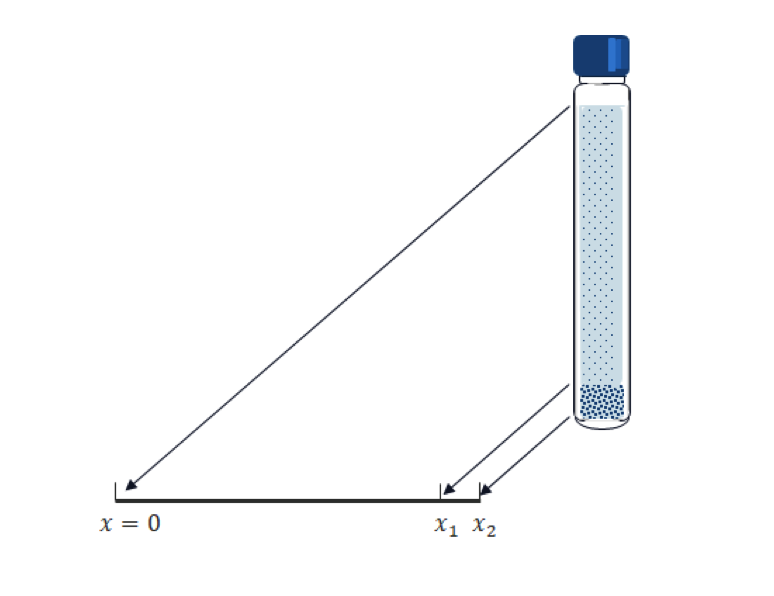
Transposing the vertical position into the x coordinate in 1D; and for a given tube length, x_2; and the computational time, T, we have the following Mason–Weaver equation:
where c is the particle concentration, the solved-for variable; A and B are the diffusion coefficient and sedimentation speed of the particles, respectively; and g is the acceleration due to the gravity.
The boundary condition at the top and bottom of the tube is the so-called zero flux boundary condition, i.e.,
This condition means that the total mass flux (not only the diffusive flux) on the boundary is zero; that is, sinking particles accumulate at the bottom since they cannot exit the test tube there. Our main interest is the amount of accumulated mass of the particles. We need to set an imaginary volume (segment in 1D) for the sake of measurement. In the above geometry, the interval [x_1. x_2] is prepared for this purpose. Note that the calculated accumulated mass is varied by the size of the interval.
The initial condition is typically a uniform distribution, as follows:
where c_0 is a constant function.
Now, we have all of the formulations for simulating sedimentation.
The Mason–Weaver equation is an easy equation to understand and solve, except for extremely fast sedimentation cases. Let’s try to explain what it physically means. It is made up from two equations:
- Diffusion (2nd term)
- Convection due to gravity (3rd term)
The interpretation of this equation would be quite easy if you imagine each phenomenon separately. Heavy particles sink quickly — almost without diffusing — and accumulate at the bottom of the test tube. Initially, the particles are uniformly distributed. As sedimentation starts, the particles disappear from the top and the number of particles increases around the bottom. At the end, almost all of the particles are found at the bottom, which means that the concentration function becomes like the delta function at the bottom of the tube. Lighter particles tend to float in the solution, as they are not affected by gravity. These two phenomena occur simultaneously in reality. The following animations show two extreme cases as examples.
Comparison of the spatial concentration profile for heavier particles (left) and lighter particles (right).
Sedimentation App for Particles with a Size Distribution
The above picture is relatively simple. In the real world, however, particles are generally not floating individually in the solution and typically make agglomerates of different sizes depending on the surface electric charges or some binding mechanisms that the particles may have. In the solution, agglomerates with a different size behave differently, as we saw in the above animation. Therefore, it is no longer easy to imagine how the overall concentration profile looks. The Mason–Weaver equation for a single particle size can be easily simulated by using the Partial Differential Equations (PDE) interface in the COMSOL Multiphysics® software user interface (UI), but it’s not easy to simulate more practical cases where you have to consider particle size distribution or some other conditions or constraints. In such cases, making an app gives you more flexibility and more satisfactory results.
In the following section, some, but not all, of the key steps to make an app that reproduces the same results as the referenced paper by DeLoid will be shown.
Step 1
Set up your geometry, materials, basic physics, and initial and boundary conditions in the Model Builder.
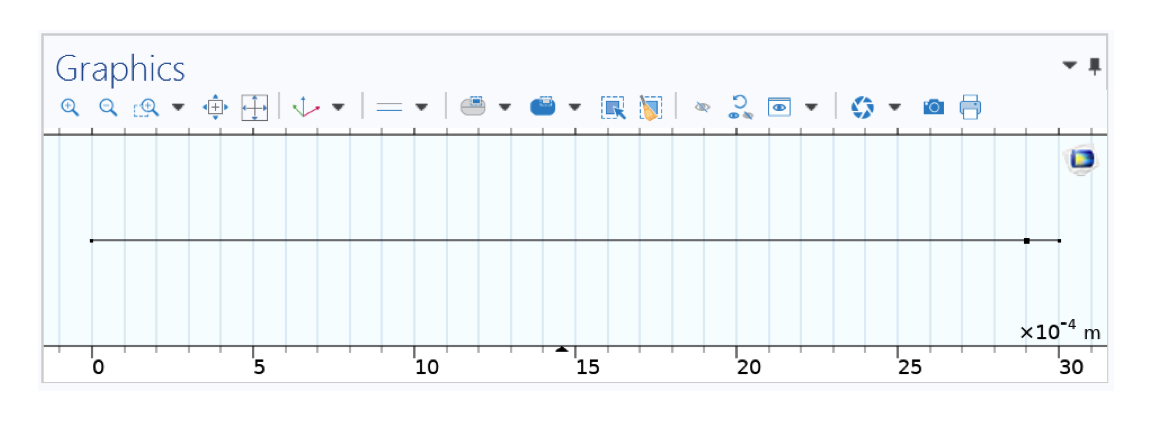
Geometry in 1D representing your test tube (cap on the left, bottom on the right).
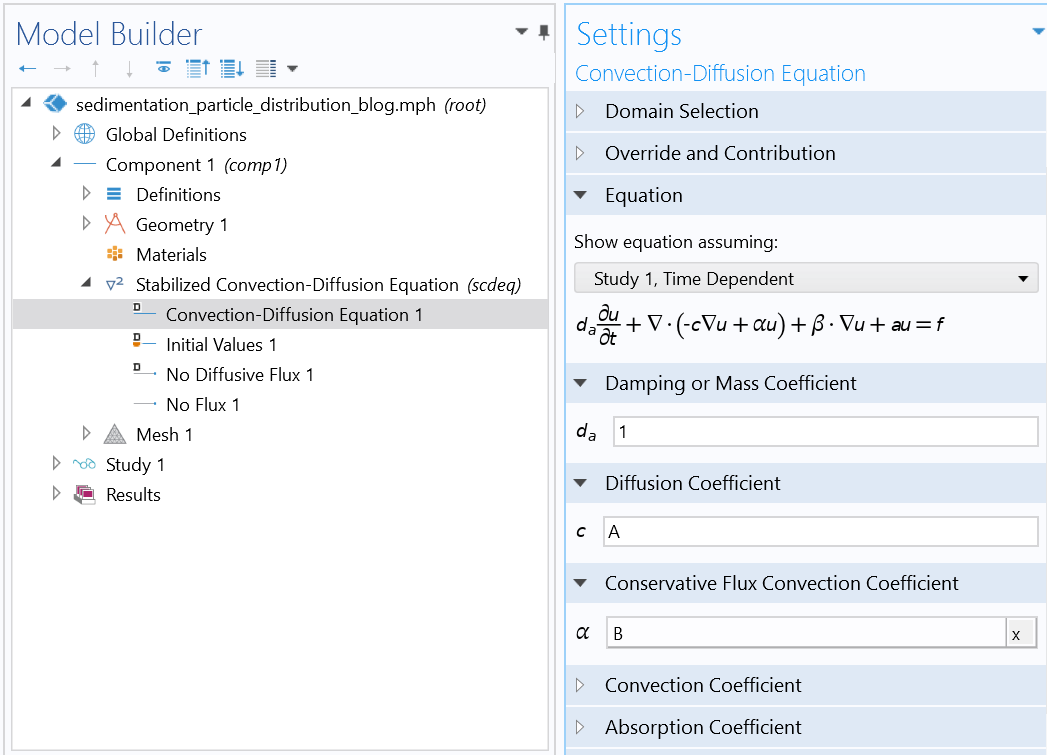
Settings of the Mason–Weaver equation using the Stabilized Convection-Diffusion Equation interface from the Classical PDE interfaces.
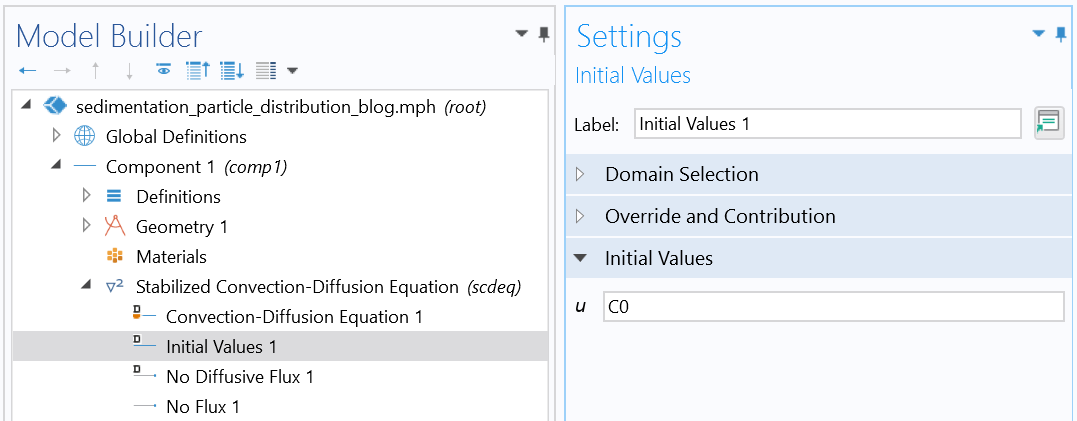
Initial condition (uniform distribution).
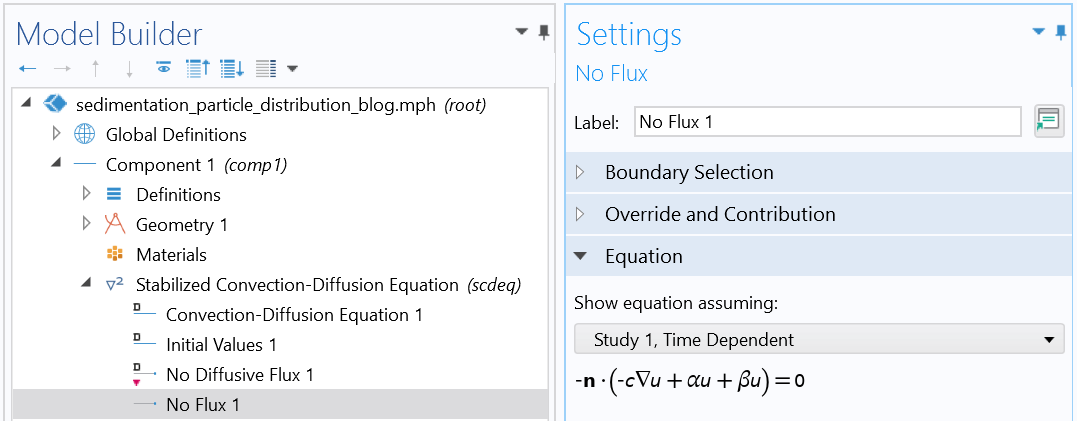
Boundary condition (reflective boundary condition).
Step 2
Make your own UI in the Application Builder.
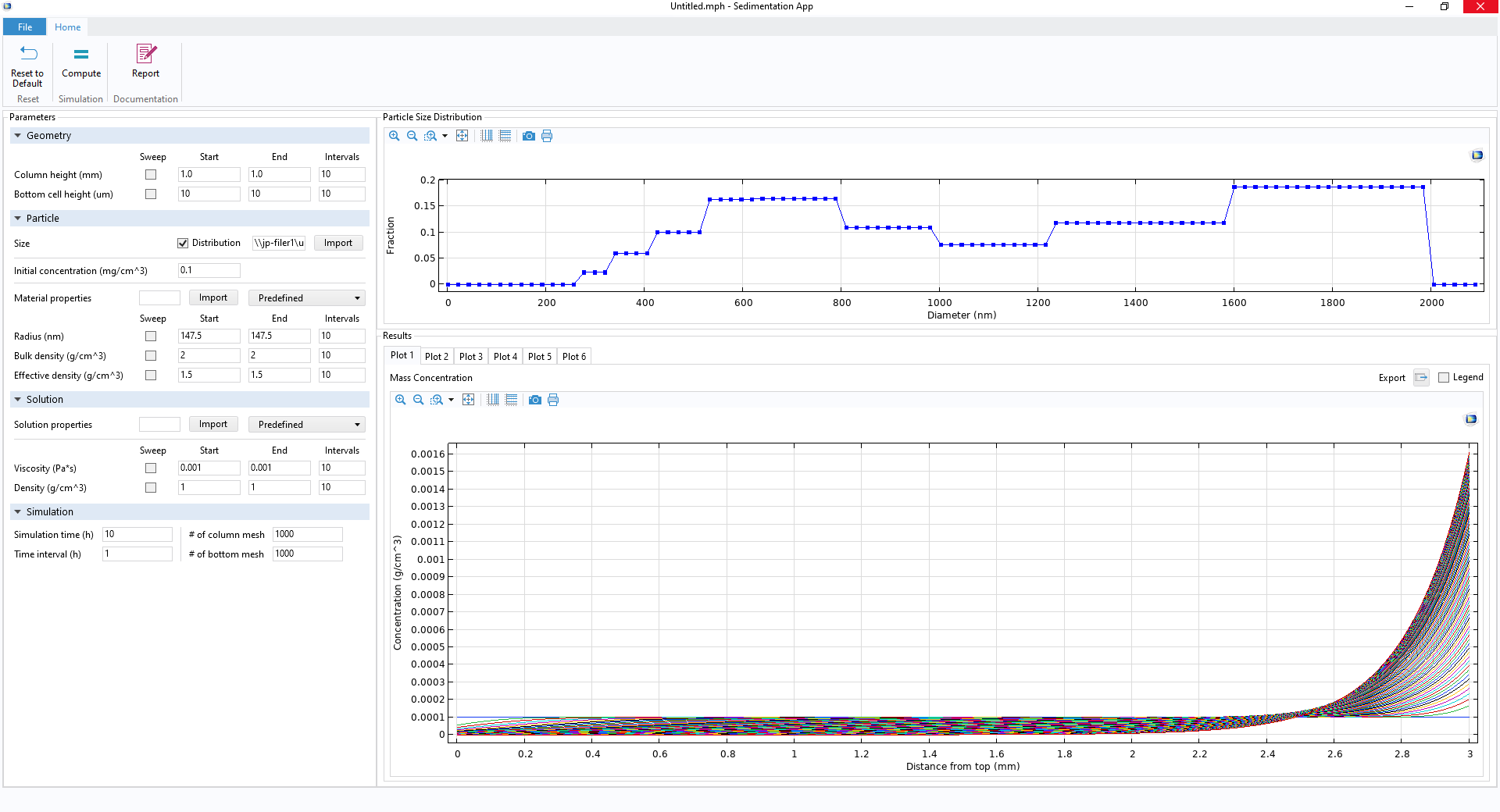
Your own app’s UI, including a few ribbon buttons (top), Parameter Setting window (left), particle size distribution profile (upper right), and Results Graphics window (lower right).
Step 3
Write Java® codes.
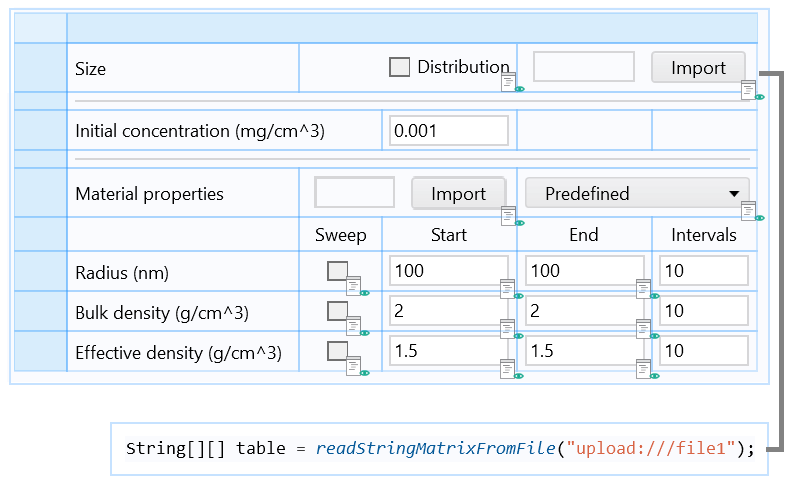
Part of the form including an Import button associated with a Java method, which loads the particle size distribution data from a file and stores it in an Array 2D String.
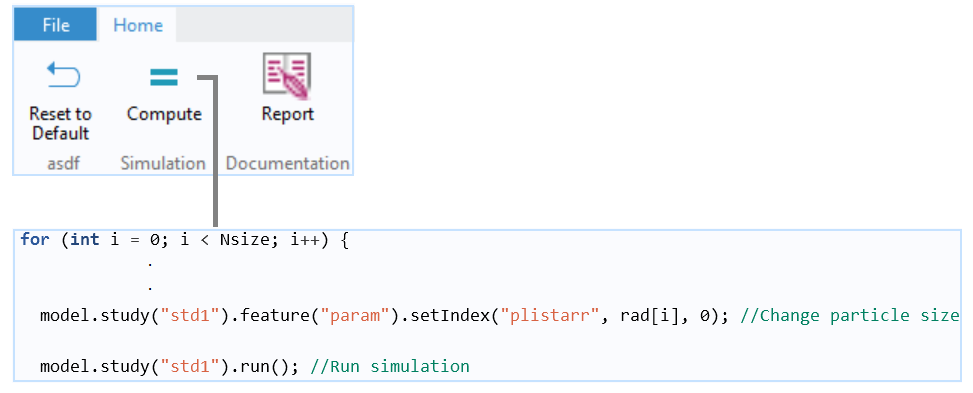
A Java method for the main for-end loop that repeats a run for each updated particle size. The particle mass in the bottom part is calculated for each particle size at each time step and stored in an Array 2D Double (not shown). At the end of the run, the particle mass is summed up to calculate the total mass fraction that accumulates in the bottom part.
With this app made by following the above steps, you can get the final results shown below, for example. The particle used in this example is CeO2, which is relatively heavy and tends to quickly sink and accumulate at the bottom, as shown in the plot below (blue line). The particle size affects the mass fraction significantly. Smaller particles tend to float by diffusion and never sink all the way. As a result, the mass fraction reaches a plateau more slowly, at less than 100%, when the size distribution is taken into account.
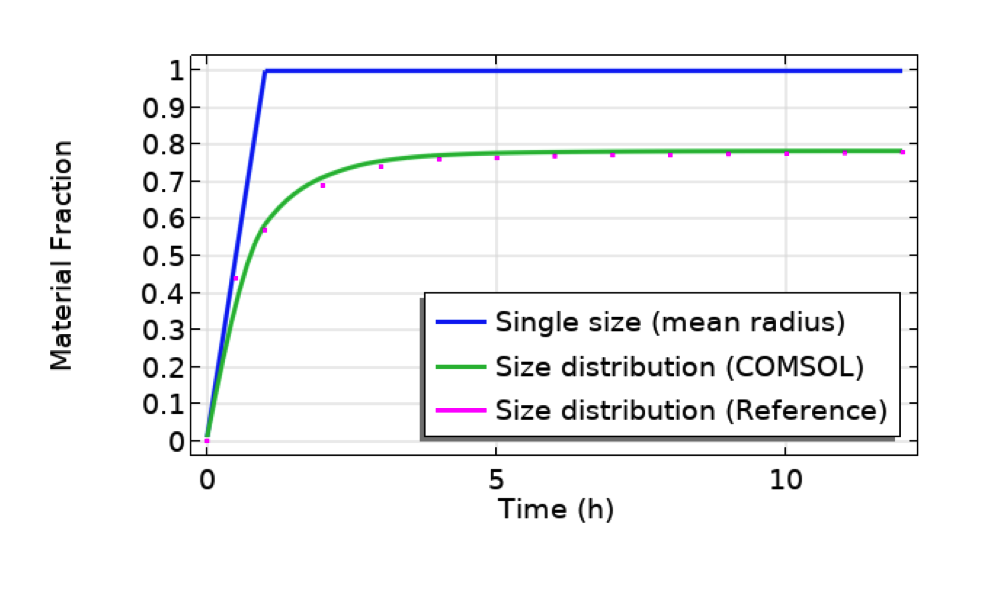
Comparison between cases for single particle size (mean radius, 491 nm, of the distribution profile shown in the previous figure of the UI) and size distribution (COMSOL Multiphysics vs. reference paper showing a good agreement). Particle: CeO2. Test tube length: 10 mm. Bottom part length: 10 um.
Additional Remarks
The coefficients A and B can be given experimentally or be calculated from the material properties by the following relations derived from fluid dynamics.
where k_B, \ T, \ \eta, \ r are the Boltzmann constant, temperature, dynamic viscosity of the solution, and the radius of the particle, respectively, and \rho_e and \rho_s are the effective density of the particle and the density of the solution, respectively.
To augment this app, you may want to modify or add more features. For pharmaceutical or biomedical applications, you may want to consider the solvability of particles. On the bottom boundary, you may want to consider another boundary condition that accounts for the adsorption and desorption instead of the reflective boundary condition. These augmentations can be done by adding an auxiliary equation. See Christmann, Ramteke, and Dokoumetzidis for reference.
Next Step
Explore the sedimentation app discussed in this blog post by clicking the button below. Use it as inspiration for building your own app, and let us know about your experience in the comments!
References
- G.M. DeLoid et al., “Advanced computational modeling for in vitro nanomaterial dosimetry”, Particle and fibre toxicology, vol. 12, no. 1, pp. 1–20, 2015.
- K. Christmann, Introduction to Surface Physical Chemistry, Springer Science & Business Media, vol. 1., 2013.
- K.H. Ramteke et al., “Mathematical models of drug dissolution: a review”, Sch. Acad. J. Pharm, vol. 3, no. 5, pp. 388–396, 2014.
- A. Dokoumetzidis and P. Macheras, “A century of dissolution research: from Noyes and Whitney to the biopharmaceutics classification system”, International Journal of Pharmaceutics 321.1-2 (2006): 1–11.
Oracle and Java are registered trademarks of Oracle and/or its affiliates.



Comments (0)