
In structural mechanics, you may want to specify user-defined material models in your simulation. COMSOL Multiphysics® software version 5.2 enables you to access material models derived from external libraries as well as material functions programmed by yourself. We demonstrate how the new functionality works with the example of implementing Mazars’ model to describe damage to concrete.
A New Method for Specifying User-Defined Material Models
In COMSOL Multiphysics, you can access a variety of predefined materials to model mechanical deformation in solids. Material models for plasticity, viscoelasticity, creep, and hyperelasticity are just some of those that are available.
By using the built-in constitutive laws as a starting point, you have the ability to create your own material models based on stress or strain invariants, flow rules, or creep laws directly in the user interface. Extra PDEs or distributed ODEs can also extend a given material law. But what if your material model includes nonlinear expressions that are impossible to express in terms of standard variables, invariants, or additional PDEs?
The latest version of COMSOL Multiphysics — version 5.2 — features a new way for you to specify user-defined material models. In structural mechanics analyses, you are now able to completely define a nonlinear stress-strain relationship, or include an inelastic strain contribution with an existing elastic material. Two new features in the Solid Mechanics interface complement this functionality: the External Strain subnode under the Linear Elastic Material node and the External Stress-Strain Relation material model.
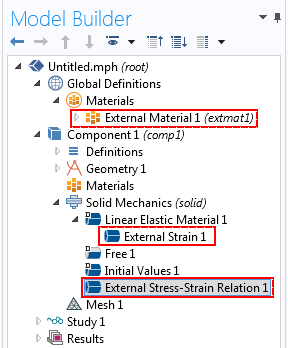
The External Material, External Strain, and External Stress-Strain Relation nodes in the model tree.
With the added capabilities, implementing external material functions coded in the C programming language is possible. If you write a wrapper function in C code, material functions can also be written in other programming languages, making it easy for you to reuse your legacy code.
Along with programming your own material models, distributing your models to colleagues and customers as add-ons is now an option as well. You can even create easy-to-use apps, by using the Application Builder and incorporating your external material functions, and distribute these to your colleagues and customers as well.
Putting the Added Functionality into Practice
To show you how the functionality works, we have added a tutorial to our Application Gallery that features a series of relevant demonstrations. The examples include a model file, a source C file, and a shared dynamic-link library (DLL) compiled and linked for a 64-bit Windows® operating system. (Running the models on Linux® operating systems and Mac OS X requires additional compilation and linking.)
In the first case, we explain how to write the C code for an isotropic linear elastic material and compare our results to the built-in Linear Elastic Material for a simple uniaxial test. The second, and more realistic, case shows how to implement a nonlinear material model that computes damage in concrete.
Let’s take a closer look at the latter of these two examples.
Using Mazars’ Damage Model for a Concrete Analysis
The deformation of brittle materials under mechanical loads is characterized by an initial elastic deformation. Upon unloading, the material will return back to its original state. However, if a critical stress or strain level is exceeded, a nonlinear fracture phase will follow the elastic phase.
As the critical value is reached, cracks will begin to grow and spread until the material fractures. The occurrence and growth of the cracks play an important role in the failure of concrete structures, and there are a number of theories used to describe such behavior. In the continuum damage mechanics formalism, a “damage” variable represents the amount of deterioration due to crack growth. The damage variable controls the weakening of the material’s stiffness.
Mazars’ model for concrete damage characterizes the fracture behavior within concrete using an isotropic scalar damage variable d. The variable enters the constitutive stress-strain relationship as
Here, \sigma is the stress tensor, C is the elasticity matrix, and \epsilon is the strain tensor.
The material, which behaves as a linear-elastic solid, is undamaged when the damage variable equals zero and fully damaged as the variable approaches one.
The inception and evolution of the damage variable is quite tricky to compute with standard variables in COMSOL Multiphysics. How so? It requires memorizing previous steps and conditional manipulation of variables based on principal stresses and principal strains. To overcome this limitation, we implemented Mazars’ damage model in an external material function, adding the C code for inspection and modification. The C code includes the definition of a number of variables, for loops, and the use of state variables to memorize damage from previous steps.
The external material function to compute Mazars’ damage model contains just over one hundred lines of code.
The plot below shows the computed uniaxial stress-strain response using Mazars’ damage model. The results are in excellent agreement with those findings presented in the book Mechanical Behavior of Concrete.
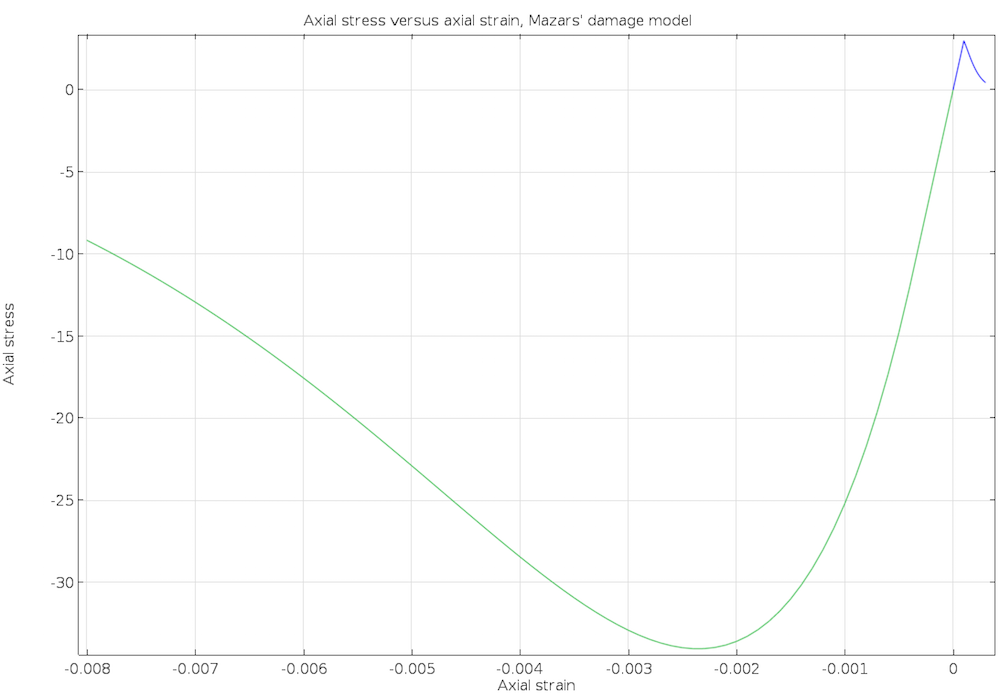
Uniaxial stress-strain response plot.
Next Steps
- Download the tutorial: External Material Examples, Structural Mechanics
- For more details on how to compile the C code for different operating systems, see the section “Working with External Materials” in the COMSOL Multiphysics Reference Manual
- Interested in learning more about Mazars’ damage model? Check out the following articles:
- J. Reynouard et al., “Modeling the Macroscopic Behavior of Concrete”, in Mechanical Behavior of Concrete, ed. J. Reynouard, J. Torrenti, and G. Pijaudier-Cabot. 63-119, Wiley 2010
- J. Mazars et al., “Local Second Gradient Models and Damage Mechanics: 1D Post-Localization Studies in Concrete Specimens”, in Bifurcations, Instabilities, Degradation in Geomechanics, ed. G. Exadaktylos and I. Vardoulakis. 127-142, Springer 2007
Microsoft and Windows are either registered trademarks or trademarks of Microsoft Corporation in the United States and/or other countries.
Linux is a registered trademark of Linus Torvalds.
Mac OS is a trademark of Apple Inc., registered in the U.S. and other countries.




Comments (21)
Krishna Kumar Soundararajan
March 24, 2016Good! However, how can I implement an elasto-plastic constitutive model with external material model?
Shyam Kishor
May 26, 2022Krishna, Have you got your answers? I am also interested in knowing this.
Henrik Sönnerlind
May 13, 2016An elasto-plastic model can be implemented using ‘External Strain’. The external strain entry is used to return an inelastic (i.e. plastic) strain ‘e_inel’, so that the stress ‘s’ is computed by
s=C:(e-e_inel)
where ‘C’ is the elasticity tensor and ‘e’ is the total strain. This is similar to how the built-in plasticity models work if you look at them in Equation View.
Note however that you have rather large flexibility already without coding through the User Defined yield functions and plastic potentials.
vikash kumar
February 10, 2017sir
i want to simulate uni axial compression test of polymers (ABS material), further i want stress -strain curve of material . how can i get it?
your response will be highly appreciated
Ed Gonzalez
February 10, 2017Vikash, please take a look at this post
https://www.comsol.com/blogs/introducing-nonlinear-elastic-materials/
Ed
Zhipeng Pi
August 3, 2017how to compile the c code to a dll file? I try to compile the C code-‘ Mazars_Damage.c’ into a dll file by using the visual studio 2013, however, the comsol cannot study and report error like ” Feature: Compile Equations: Stationary (sol1/st1)
Error in multiphysics compilation.
Error initializing external variables interface.
– Function: eval”
why?
Ed Gonzalez
August 23, 2017Zhipeng, please contact our support team in your country.
Greetings
Ed
KAI REN
November 22, 2017Thanks!
If I want to build a temperature-dependent elasto-plastic constitutive model, how can I use this method? Thank you!
KAI REN
November 22, 2017Thanks!
If I want to build a temperature-dependent elasto-plastic model for thermal stress study, how can I use this method? Thank you!
Ed Gonzalez
November 22, 2017Hi KAI REN,
Please take a look at the post
https://www.comsol.com/blogs/how-to-implement-elastoplasticity-in-a-model-using-external-materials/
KAI REN
November 22, 2017Hi Dr. Ed Gonzalez,
Thanks for your reply!
I have a question about transferring strain fields between two different mph files. Is this method can be used to transfer strain field in different mph files (when thermal strain, plastic strain are involved), so the later mph file can utilize the result of the former mph file as initial value?
Thanks!
Kai
Ed Gonzalez
November 23, 2017Dear Kai,
Please contact our support team for a detailed explanation on how to transfer strain fields.
Greetings
Ed
https://www.comsol.se/support
Yu Zhang
January 21, 2020Hi, Ed,
In your model, the Jacobian is defined as “s=D(d):e”. However, according to the HELP document, the Jacobian should be defined as “ds=D'(d):de”. D(d) and D'(d) are not equal to each other. Why D(d) is used in your code? Could you please clarify it? Thanks a lot for your help.
Ed Gonzalez
January 24, 2020 COMSOL EmployeeHi Yu, this simple example was meant to introduce the use of External Materials to our users. The idea was to keep the code as simple as possible. You can read more about how stress update algorithms define the Jacobian in this post:
https://www.comsol.com/blogs/how-to-implement-elastoplasticity-in-a-model-using-external-materials/
Greetings
Ed
Manik Kumar
December 27, 2017Dear,
I am currently on magnetostrictive materials. For which we developed the constitutive model for magnetostrictive material but we made a code in MATLAB. SO first we have to convert our MATLAB code to C or directly MATLAB code can be imported to COMSOL.
Manik Kumar
December 27, 2017Dear,
If anyone has suggestions for the previous comment please reply at the earliest.
Caty Fairclough
January 25, 2018Hi Manik,
Thanks for your comments!
For questions related to your modeling, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
Shyam Kishor
May 26, 2022Manik, Have you got the answer of your previous question?
Yu Zhang
January 5, 2019Hi, Ed Gonzalez:
Thank you for sharing us the wonderful approach. I am a bit confused by the code of this model. As given in the code, the stress is computed as “s[i] += D[i][j] * e[j];”. This is the total form of the constitutive model, which might be incorrect to determine the stress tensor when the D[i][j] is updated in each step due to damage. The increment form, like “ds[i] += D[i][j] * de[j]; s[i]=s_previous[i]+ds[i]”, may be more appropriated to determine the stress tensor. I am not sure whether there is any specific treatment about your model after you embedded it into COMSOL.
Would you mind give me some ideas how your model works in the COMSOL, and give some comments on my approach.
Any help would be highly appreciated.
Yu
Ed Gonzalez
January 7, 2019Hi Yu Zhang, please take at our blog about how to implement an elastoplastic material, you can also find the example code therein.
Greetings
Ed
https://www.comsol.com/blogs/how-to-implement-elastoplasticity-in-a-model-using-external-materials/
Debdutta Ghosh
July 29, 2019How to plot the function Undamaged_Elastic_Modulus (S_dmg) of Mazar’s model ?
By default there options are available to plot the young’s modulus. If there are options available to plot any desired parameters of any damage model, kindly show the procedures to do so.