
Metamaterials are artificial materials with properties that rely on a particular structural design rather than chemistry. Their structure is often complicated, making these materials challenging to fabricate. Here, we present numerical research that investigates one such material — a poroelastic metamaterial (made from a single material with voids) with the ability to expand under hydrostatic pressure.
Combining Metamaterials and 3D Printing
Two topics frequently pop up on the COMSOL Blog: 3D printing and metamaterials. Their potential applications, such as generating customized medical implants, printing houses, and being used for cloaking technology, could transform the world around us.

A 3D printer. Image by Jonathan Juursema — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
By combining these two technologies, we might be able to use direct-laser-writing (DLW) printing to fabricate complicated metamaterials, a process that could be challenging or impossible with other manufacturing techniques. Using this idea as inspiration, a team from the Karlsruhe Institute of Technology (Germany) and Université de Bourgogne Franche-Comté (France) investigated a metamaterial that displays the unique mechanical property of negative effective compressibility under stable and static conditions.
Studying a Poroelastic Metamaterial with a Negative Effective Compressibility
The researchers’ poroelastic metamaterial is a 3D manmade composite that experiences isotropic expansion when the hydrostatic pressure generated by the surrounding environment is increased. Most natural elastic materials react in the opposite way, reducing their volume when exposed to an increased hydrostatic pressure at a fixed temperature.

A sponge is a material that is affected by poroelastic phenomena.
So why does this metamaterial expand? To answer this, let’s take a look inside the metamaterial, which consists of a single ordinary constituent solid. Within the material are hollow 3D crosses with concealed internal volumes that contain air at a constant pressure. Each cross also has circular membranes attached to its ends.
These membranes warp inward or outward when the surrounding pressure is different than the pressure within the crosses. The bars asymmetrically connected to the membranes translate this warping into a cross rotation. If the hydrostatic pressure outside is greater than the pressure inside, then the individual rotations translate into an isotropic expansion of the structure, causing a negative effective compressibility.
A unit cell at zero pressure (left) and an elevated pressure (right), depicting the principle of negative compressibility. Image courtesy Jingyuan Qu and Muamer Kadic.
While this negative compressibility may appear to violate the laws of physics, the effective volume increase corresponds with an unseen volume decrease within the material. This ensures that the structure is stable.
Analyzing an Innovative Poroelastic Metamaterial with COMSOL Multiphysics®
To examine the detailed structure of the innovative metamaterial, the researchers turned to the COMSOL Multiphysics® software. When asked about the benefits of this approach, Jingyuan Qu — a member of the research team — noted how easy it was to implement.
The model of the metamaterial is a single unit cell. To see what happens when there is a difference between the pressure inside and outside the material, a pressure increase is implemented as a normal force on all of the outer surfaces of the model. Further, the model is simulated under periodic boundary conditions, enabling the researchers to successfully find the effective material parameters.
Note that built-in periodic boundary conditions are available in the Structural Mechanics and MEMS modules.
For their research, the team performed two main numerical experiments:
- A finite-size study (one unit cell) with natural boundary conditions at the end (free)
- A (hypothetically) infinitely extended case using periodicity conditions
In their experiments, the team used the equations for standard linear elasticity:
0 = \nabla\cdot \sigma + \mathbf{F}_V \\
\sigma = \mathbf{C}\colon\epsilon \\
\epsilon = {\frac{1}{2}}[{(\nabla\mathbf{u})}^{T}+(\nabla\mathbf{u})]
\end{array}
Now, let’s take a look at the second numerical experiment.
Using Periodic Boundary Conditions
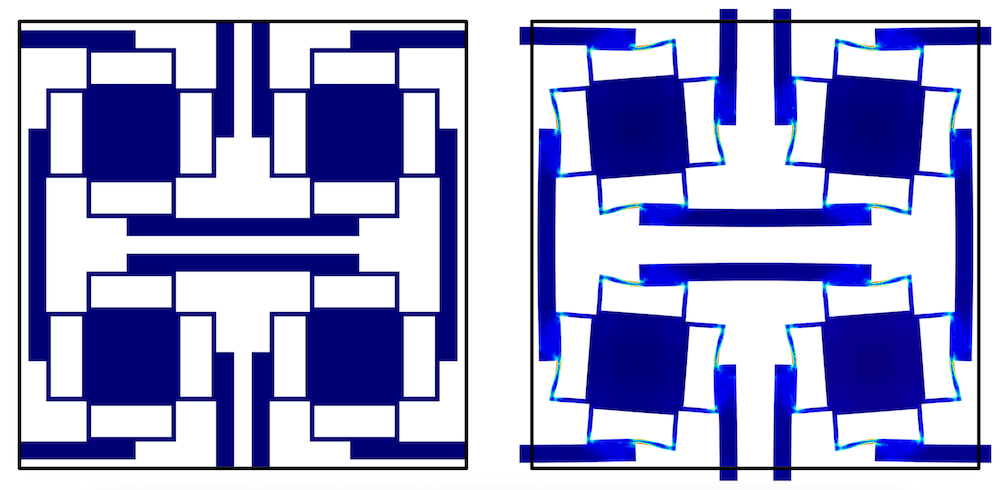
To mimic an infinite material case, periodic conditions are implemented so that each side of the unit cell must contract or expand isotropically. First, selections for each side of the structure are created and named according to the directions x+, x-, y+, y-, z+, and z-. Then, probe variables were created, giving the average displacement on the “minus” sides (dispx, dispy, dispz), shown in the second screenshot below.
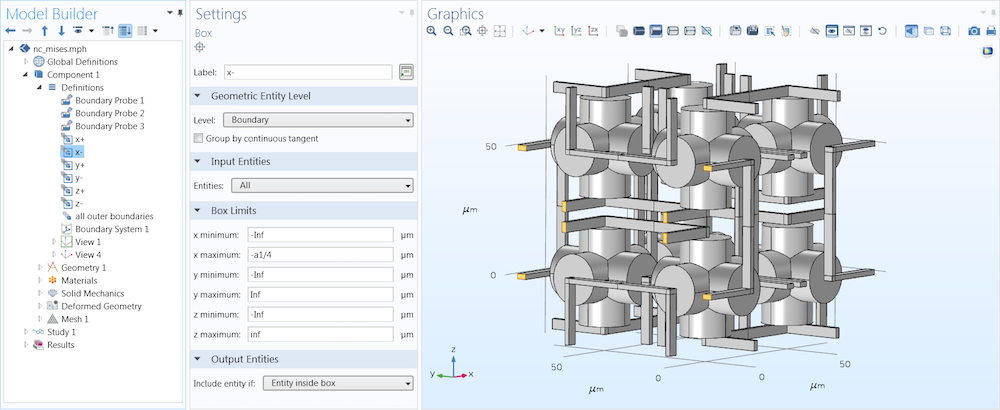
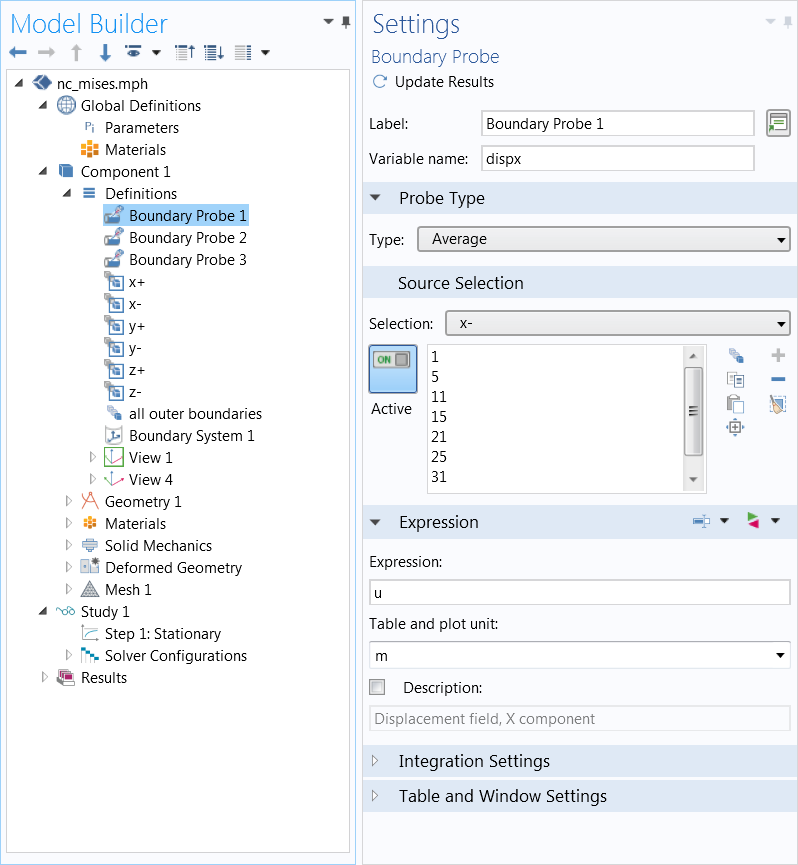
Examples for the x direction case, displaying the process of selecting the boundaries that connect to the next unit cell, shown for one of the six planes (top) and the boundary probe settings (bottom). Images courtesy Jingyuan Qu and Muamer Kadic.
Next, the probe variables are used as boundary conditions on both sides (prescribed displacement). That is, on the ‘x-‘ boundaries, the x direction displacement is set to dispx, while on the ‘x+’ boundaries, it is set to –dispx. Similar boundary conditions are then set on the other periodic cuts. The idea is that the displacement dispx, still unknown, becomes part of the solution. Since the conjugate reaction force to the prescribed displacements must be zero, the structure will expand or contract in such a way that there is no net force.
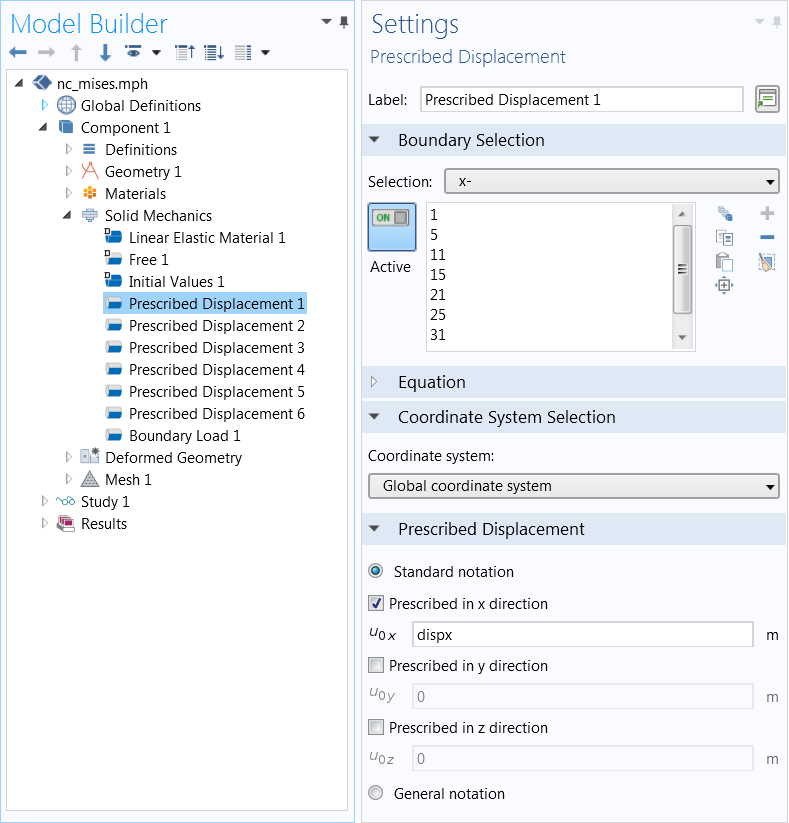
Prescribing the probed displacement. Image courtesy Jingyuan Qu and Muamer Kadic.
Moving on, outer pressure is also applied. After selecting the outer boundaries of the geometry and using a high angular tolerance, the model shows that the inner boundaries in the concealed volumes are not selected, as seen below.
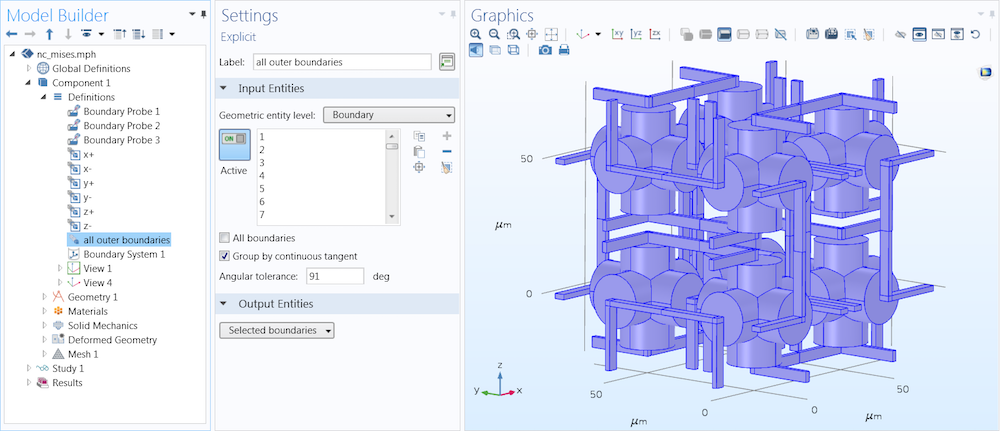
The outer boundary settings. Image courtesy Jingyuan Qu and Muamer Kadic.
The hydrostatic load is then applied as a boundary load with pressure (P).
S\cdot\mathbf{n}= {\mathbf{F}}_{A} \\
{\mathbf{F}}_{A}=-P\mathbf{n}
\end{array}
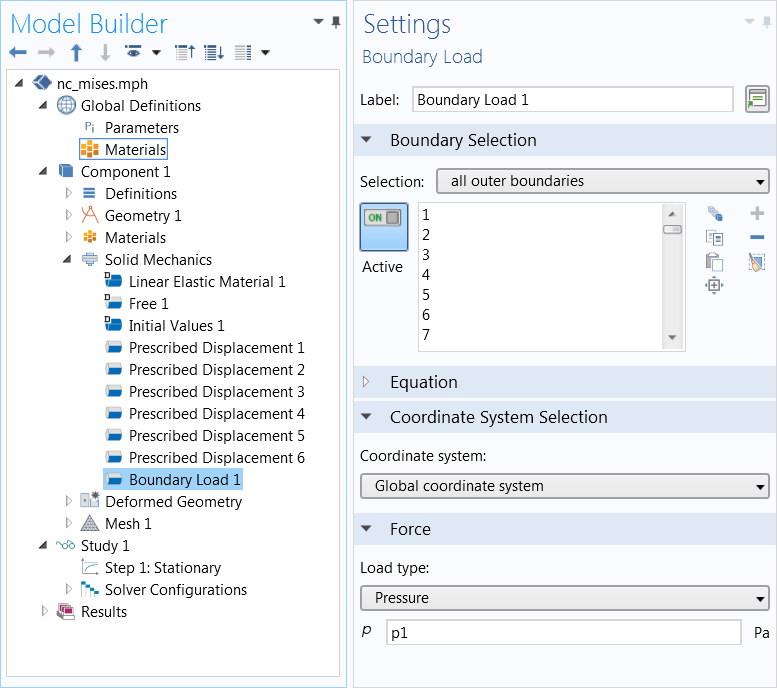
The hydrostatic pressure is implemented as a normal force acting on all outer boundaries. Image courtesy Jingyuan Qu and Muamer Kadic.

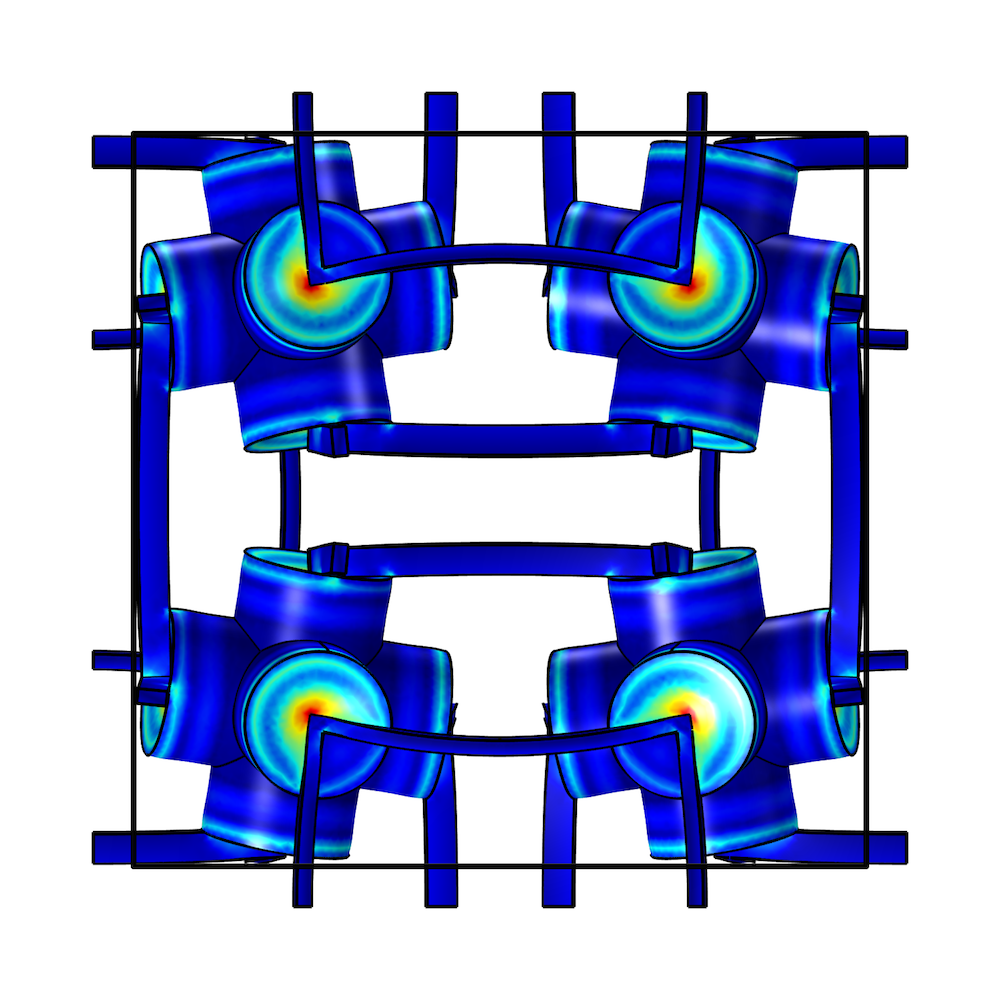
The resulting structure of the poroelastic metamaterial at different angles. Images courtesy Jingyuan Qu.
As a point of comparison, the researchers also examined an ordinary porous structure and a cube of a continuous isotropic material. When exposed to an increased hydrostatic pressure, both of these structures shrink in volume. Under the same conditions, the porous metamaterial expands — highlighting its negative effective compressibility.
Next Steps
Thanks to their extensive research, the team was able to capture the metamaterial’s behavior, improve its design, and use this information to move on to the fabrication stage. While fabricating this material may not be possible with conventional machining techniques, 3D printing serves as an alternative option for creating negative compressibility metamaterials. 3D printers can form this metamaterial by using ordinary materials that shrink under hydrostatic pressure.
Qu notes that after it is realized, the metamaterial may find uses in high-pressure applications due to its ability to maintain a constant effective volume, even when subjected to high-pressure environments.
Find Out More About Metamaterials
- Check out the researchers’ original work:
- Read their full paper, “Poroelastic Metamaterials with Negative Effective Static Compressibility“
- View a Phys.org article on this metamaterial
- Read these metamaterial-related blog posts:



Comments (2)
Samuel Fagbemi
August 8, 2017Hi, thanks for your blog post. I’m currently trying to generate meshes for a complex poroelastic shape. The RVE (my unit cell) is super irregular but I was thinking of creating a duplicate of the sample and mirroring it about the axis on the face opposite to the reference point in order to make opposite surfaces identical hence apply PBC. Even after doing this, I keep running into problems with COMSOL and it tells me that it can’t apply PBC on curved surfaces. Please how do you advise I go about this?
Caty Fairclough
August 23, 2017Hi Samuel,
Thanks for your comment!
For questions related to your modeling, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com