
The foundation of a tunnel, dam, building, or other structure can be analyzed with a method called triaxial testing. Performing triaxial tests before, during, and after construction helps to ensure that structures are safe and reliable. To better understand the mechanics of soil and improve a structure’s stability, you can model the loading and unloading curves for a triaxial testing apparatus and test the soil’s model parameters in the COMSOL Multiphysics® software.
What Is Triaxial Testing?
Triaxial testing is a method used to determine the stress-strain properties of soils by subjecting soil samples to constant lateral pressure while increasing vertical pressure. This test measures stresses in three mutually perpendicular directions.
The mechanical behavior of a rock, sand, or soil sample can be complicated to analyze, depending on the specimen. Even if the soil seems stable at first, the construction process can subject it to shifts and uneven settlements later on. Just look at what happened to the Tower of Pisa. This popular tourist destination was built on softer ground (clay, sand, and shells), which shifted over time and caused the tower to lean off-kilter.

The Leaning Tower of Pisa, Italy. Image by Alkarex Malin äger — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
A triaxial test obtains the shear strength parameter measurements needed for a construction project. One of the reasons why triaxial testing is so common is because of its versatility. During the procedure, you are able to control drainage; measure pore water pressures, stress, and strain; increase loads; and observe deflections until sample failure.
In a typical triaxial test, the soil sample is placed inside a rubber membrane and then axially compressed while maintaining a constant radial pressure. If the soil is cohesive, you can prepare the samples directly from saturated, compacted samples. If the soil lacks cohesion, you can use a mold to keep the shape needed for the test.
There are three main triaxial tests:
- Consolidated – Drained (CD): The sample is consolidated and sheared in compression slowly, allowing the pore pressures to dissipate and the sample to adjust to the surrounding stresses.
- Consolidated – Undrained (CU): The sample is not allowed to drain and is assumed to be fully saturated. Pore pressures are measured to approximate the consolidated-drained strength.
- Unconsolidated – Undrained (UU): The sample is compressed at a constant rate, and loads are applied quickly, giving the sample no chance to consolidate.
The Many Applications of Triaxial Testing
Triaxial tests have a wide variety of application areas. For instance, triaxial testing is used in the oil and gas industry to determine the properties of shale cores and predict how soil responds during natural gas extraction. Also, triaxial shear tests are used for building dams and embankments. For applications such as underground expansion in cities as well as commercial and residential construction, triaxial testing is performed before excavation.
One advantage of triaxial testing is the adaptable machinery design, which includes many modification options. If you are testing high-strength rock, for instance, you can change the cylinder sleeve material from rubber to a thin metal sheeting. You can also vary the design of the triaxial testing apparatus to account for large loads or different methods of compression.

A triaxial rock test system. Image by Jingyi Cheng, Zhijun Wan, Yidong Zhang, Wenfeng Li, Syd S. Peng, Peng Zhang — Own work. Licensed under CC BY 4.0, via Wikimedia Commons.
How does triaxial testing apply to other environmental conditions that are harder to predict, like seismic shifts? During an earthquake, for instance, the mechanical behavior of soil can change considerably. The type of change it undergoes depends on several variables, such as:
- Duration and intensity of the quake
- Location of the quake
- Water table depth of the structure
In addition, earthquakes can initiate soil liquefaction. This type of quicksand can continue to cause damage long after the earthquake is over. Triaxial testing is often used to help predict structural damage in the event of a natural disaster.

Liquefaction after the earthquake in Niigata, Japan, in 1964. Image in the public domain in the United States, via Wikimedia Commons.
The Triaxial Earthquake and Shock Simulator (TESS) is an advanced example of a triaxial testing method for earthquake preparation. This device is operated by the U.S. Army Engineer Research and Development Center. TESS is able to independently control three axes at the same time, which provides more realistic earthquake conditions for engineers who want to test facilities and equipment for vulnerabilities.
Modeling the Loading and Unloading Curves for a Triaxial Testing Apparatus
Using the Geomechanics Module, an add-on to the Structural Mechanics Module and COMSOL Multiphysics, you can model a triaxial testing apparatus to examine its loading and unloading curves.
In this example, the apparatus consists of a cylinder that presses the soil sample from the top. A flexible membrane controls the surrounding pressure, which allows changes in the radial forces.
In the schematic below, you see how the different boundaries of the testing apparatus can be defined. Because the soil is subjected to loading at the top of the apparatus, the Prescribed Displacement boundary condition is used to slowly increase the vertical displacement.
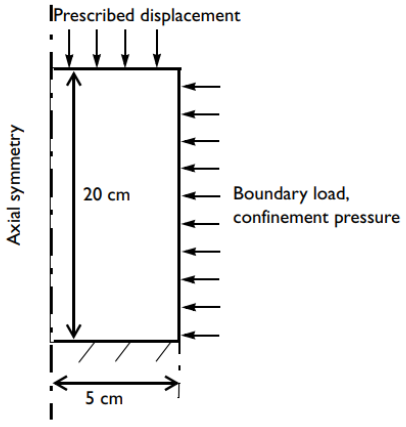
Dimensions, boundary conditions, and boundary load for the triaxial apparatus.
This model is a starting point for testing the soil’s model parameters. The soil properties are taken from a standard clay material. This example uses the Soil Plasticity feature in the COMSOL® software with the Drucker–Prager criterion.
Evaluating the Model Results
After applying a vertical displacement and a confinement pressure to the specimen sample, you can study the results of the static response and collapse load for various confinement pressures.
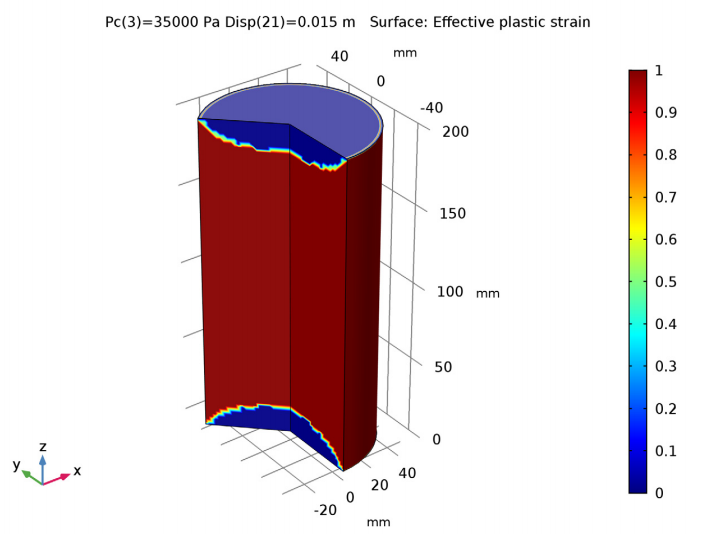
After loading the soil sample, you can look at the effective plastic strain. Most of the sample suffers from plastic deformation (shown in red), with only a small part in the elastic region (shown in blue).
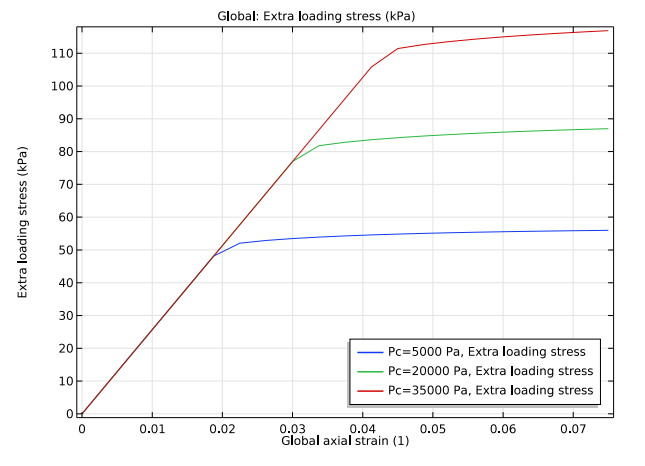
From here, you can test different confinement pressures by plotting the additional loading stress on the soil sample caused by the prescribed top displacement. Below is the extra loading stress for three different confinement pressures on the porous matrix:
Depending on the loading and draining conditions of the soil samples, you can conduct one or more of the three triaxial testing methods.
Next Steps
To get started with modeling a triaxial testing apparatus, click the button below. From the Application Gallery, you can log into your COMSOL Access account and download the MPH file for detailed instructions.
- Read more about using simulation for geotechnical applications on the COMSOL Blog:




Comments (2)
Shashank Tiwari
June 27, 2018Hello:
I am working on a poroelasticity problem and want to apply a time-dependent external stress on the poroelastic model of a cylinder. I have initialized the pore pressure in the cylinder in the “Darcy’s law” section and ran a case (coupled problem) successfully in which the external stress (in solid mechanics section) was constant.
When I run the model with a time-dependent external stress (which decreases very slowly at a rate of 0.6 psi/s from its initial value), I am not sure why the results are incorrect at t=0.
At t=0, it is expected that the slice plot of the cylinder will show “internal pressure” equal to the pore pressure and the external pressure equal to the initial value of the “external stress”. However, the result shows that the pore pressure in the cylinder is much larger than its initial value at t=0.
Could you please suggest how to apply a time-dependent external stress in such problems.
I look forward to hearing your comments.
Thanks,
Shashank
Thomas Forrister
July 2, 2018Hello Shashank,
Thanks for your comment.
For questions related to your modeling, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
Best,
Thomas