All posts by Chien Liu
How to Model the Interface Trapping Effects of a MOSCAP
Looking to analyze interface trapping effects in a MOSCAP? Learn how to use a feature in the Semiconductor Module that enables you to add charging and carrier capture/release effects to a model.
Simulating the Tunneling Current Across a Graded Heterojunction
Interested in semiconductor design? Get an intro to the theory behind quantum tunneling as well as a demonstration of simulating the tunneling current across a graded heterojunction.
Self-Consistent Schrödinger-Poisson Results for a Nanowire Benchmark
This benchmark model of a GaAs nanowire validates the Schrödinger-Poisson Equation multiphysics interface, which is useful for modeling systems with quantum-confined charge carriers.
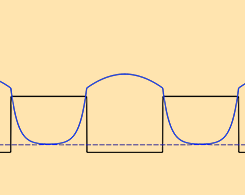
Computing the Band Gap in Superlattices with the Schrödinger Equation
You can easily compute the effective band gap for a superlattice structure by using a predefined Schrödinger Equation interface and building a simulation application.
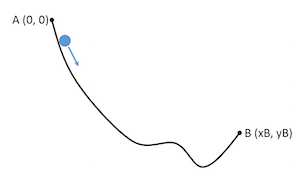
How to Solve for the Brachistochrone Curve Between Points
The shortest route between two points isn’t necessarily a straight line. If by shortest route, we mean the route that takes the least amount of time to travel from point A to point B, and the two points are at different elevations, then due to gravity, the shortest route is the brachistochrone curve. In this blog post, we demonstrate how to use built-in mathematical expressions and the Optimization Module in COMSOL Multiphysics to solve for the brachistochrone curve.
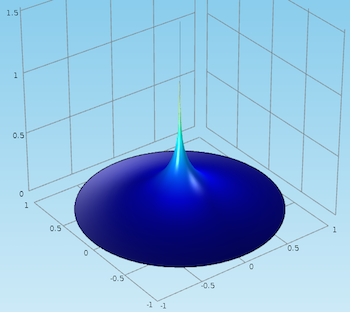
How to Implement a Point Source with the Weak Form
Today we continue our discussion on the weak formulation by looking at how to implement a point source with the weak form. A point source is a useful tool for idealizing the situation where a source is concentrated in a very small region of the modeling domain. We will find that it is very convenient to set up such a point source using the weak form.
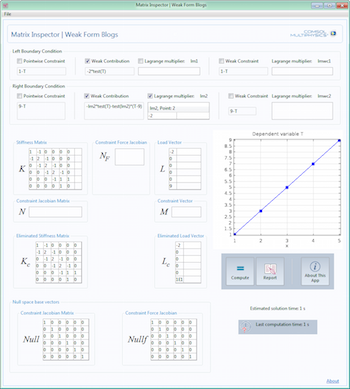
Implementing the Weak Form with a COMSOL App
Previously in our weak form series, we discretized the weak form equation to obtain a matrix equation to solve for the unknown coefficients in our simple example problem. Following the same procedure as in this previous blog post, we will implement the equation in the COMSOL Multiphysics® software with additional steps included to examine the matrices. We will find it more convenient to use a COMSOL® software application to display all relevant matrices at once, arranged logically on one screen.
Can We Hear the Shape of a Drum?
Over half a century ago, Mark Kac gave an interesting lecture on a question that he had heard from Professor Bochner ten years earlier: “Can one hear the shape of a drum?” He focused on the (then undetermined) uniqueness of the set of eigenvalues given the shape of a vibrating membrane. The eigenvalue problem has since been solved and here we explore the “hearing” part of the question by considering some interesting physical effects.