All posts by Walter Frei
Model Translational Motion with the Deformed Mesh Interfaces
2 interfaces for manually defining the deformation of finite element mesh: Deformed Geometry and Moving Mesh. Learn when and how to use each in this blog post…

Improving Your Meshing with Swept Meshes
Get a demonstration of using swept meshing to generate efficient and accurate finite element meshes for some common modeling cases, such as calculating the fluid flow through a network of pipes.

Using General Extrusion Operators to Model Periodic Structures
If your multiphysics model includes a periodic solution to one physics and nonperiodic solutions to other physics of interest, you can exploit the periodicity to reduce computational requirements!

Computing Design Sensitivities in COMSOL Multiphysics
You can compute design sensitivities via the core functionality of COMSOL Multiphysics®. We show you how with a parallel plate capacitor example.
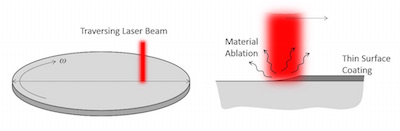
Tracking Material Damage with the Previous Solution Operator
We demonstrate how to use the Previous Solution operator to track material damage in your simulation, using an example of “baking off” of a thin coating on a wafer heated by a laser.
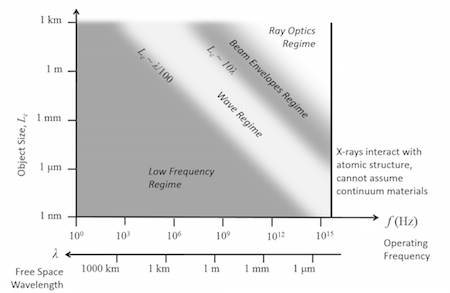
Guide to Frequency Domain Wave Electromagnetics Modeling
Read this blog post for your introduction to the various types of problems that you can solve in the RF and Wave Optics modules with COMSOL Multiphysics®.

Using the Previous Solution Operator in Transient Modeling
Use the Previous Solution operator for time-dependent models in which you want to evaluate quantities at the previous time step when using the default implicit time-stepping algorithm.
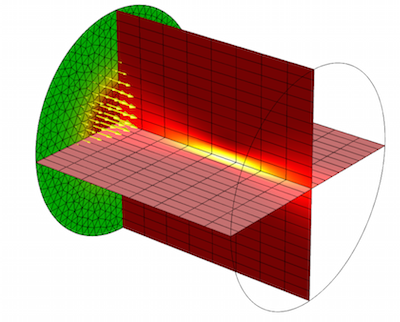
Modeling Laser-Material Interactions in COMSOL Multiphysics
When it comes to modeling laser-material interactions and heating, different modeling techniques are appropriate for different problems. We go over a few examples here >>
