
Quantum mechanics ushered in the era of modern physics, specifically during the first decades of the 20th century. It may be fair to say that no other theory has shaken our understanding of reality quite as profoundly. In this blog post, we take a look at perhaps the most significant exact results of quantum mechanics — the ground state and the first few excited states of the hydrogen atom — and go over how to reproduce these results using the COMSOL Multiphysics® software.
Quantum Mechanics and Atomic Structure
The existence and stability of atoms, which consist of a positively charged nucleus surrounded by a cloud of negatively charged electrons, cannot be explained with classical physics. A charged particle in accelerating motion (such as an electron orbiting a nucleus) should produce electromagnetic radiation, thus gradually losing energy and resulting in the inevitable collapse of the electron into the nucleus. Quantum mechanics resolves the conundrum by establishing that bound electrons can only possess certain fixed energy values, prohibiting a gradual loss of energy by radiation. This is mathematically analogous to a standing wave: the wave must be single-valued, which is possible for only certain fixed wavelengths, i.e., energies.
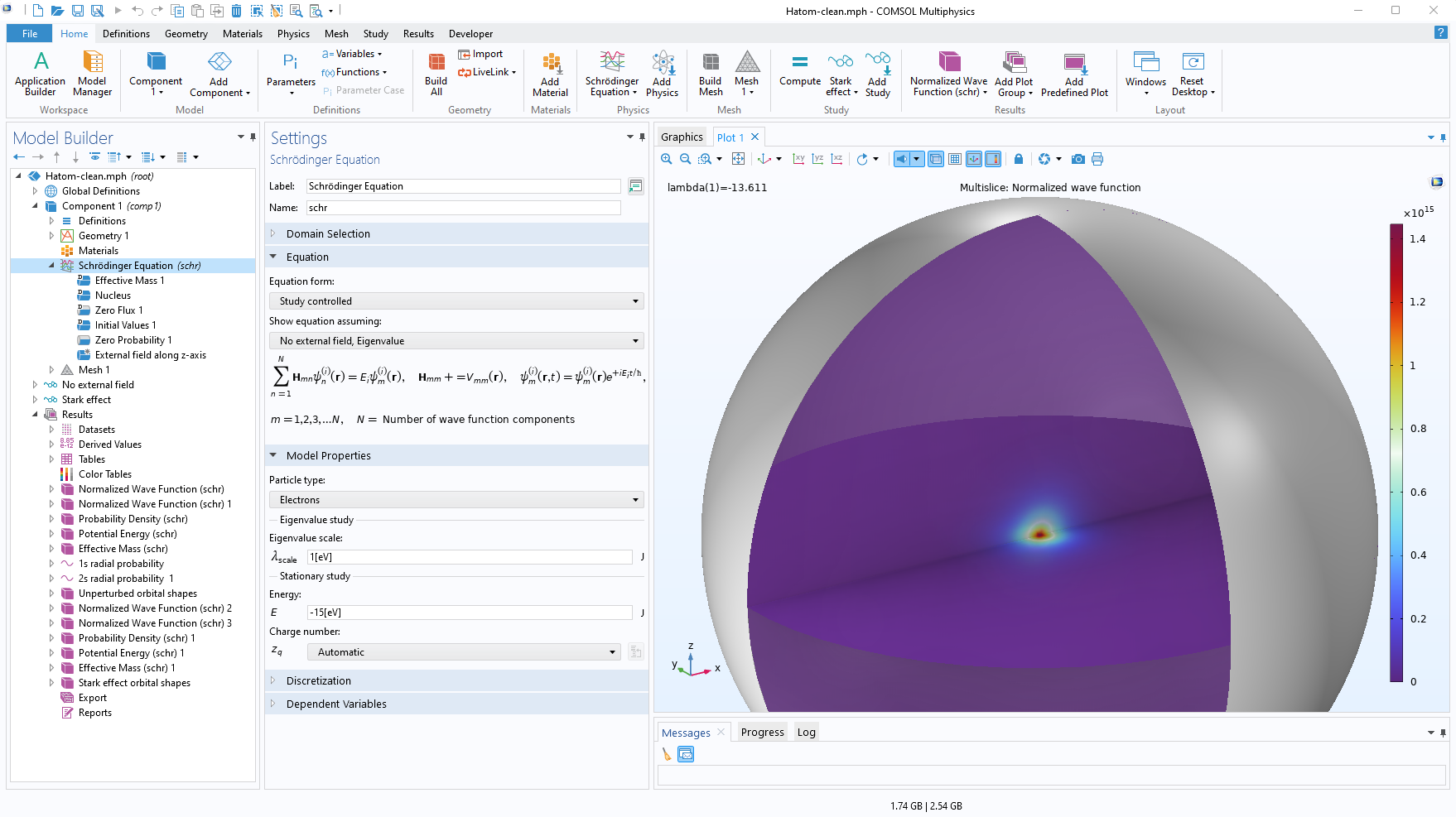
The COMSOL Multiphysics® user interface with the Graphics window showing the hydrogen atom model, discussed further in the following section.
One of the early demonstrations of the power of quantum mechanics was the experimental confirmation of the results for hydrogen (see below) by spectroscopic measurements. Since then, quantum mechanics has become the most verified theory in physics.
Unlike multielectron atoms, the hydrogen atom with its single electron is, to an excellent approximation, described by the time-independent Schrödinger equation (TISE):
Here, \hbar, m_e, e, and \epsilon_0 are the reduced Planck constant, electron mass (reduced mass), elementary charge, and the permittivity of vacuum, respectively. The dependent variable to be solved for, \psi(\mathbf{r}), is the wave function: a complex scalar field whose norm, |\psi(\mathbf{r})|^2, gives the probability of finding the electron at \mathbf{r}. The operator on the left-hand side, \hat{H}, is the Hamiltonian, which essentially corresponds to the total energy of the system. The Laplacian gives the kinetic energy of the electron, whereas the potential energy is simply given by the Coulomb potential due to the positively charged nucleus (in this case, just a single proton) at the origin. The TISE is in the form of an eigenvalue problem for the unknown total energy, E, and can be solved exactly by the usual tools of the trade: separation of variables and series expansions. The resulting eigenstates are labeled by the three integers, or quantum numbers n, l, and m, where n,l\in \mathbb{N}, l \leq n and m=-l, \cdots, 0,\cdots,l. Using spherical polar coordinates with \theta and \phi denoting the polar and azimuthal angles, respectively (same as the definition used in COMSOL®), they can be expressed as
where R_{nl} is the radial wave functions and Y_l^m(\theta, \phi) \propto P_l^m(\cos\theta) e^{im\phi}, expressed in terms of the Legendre polynomials P_l^m(\cos\theta), are known as the spherical harmonics. The eigenenergy only depends on the principal quantum number, n:
where R_H\approx13.6057\,\mathrm{eV} is known as the Rydberg constant. The explicit expressions for the first few eigenstates are given in the table below.
| Eigenstate | R_{nl}(r) | Y_l^m(\theta, \phi) |
|---|---|---|
| \psi_{100} | \frac{2}{a_0^{3/2}}e^{-\frac{r}{a_0}} | \frac{1}{2\sqrt{\pi}} |
| \psi_{200} | \frac{1}{2\sqrt{2}a_0^{3/2}}\left[ 2-\frac{r}{a_0}\right]e^{-\frac{r}{2a_0}} | \frac{1}{2\sqrt{\pi}} |
| \psi_{210} | \frac{1}{2\sqrt{6}a_0^{3/2}}\frac{r}{a_0}e^{-\frac{r}{2a_0}} | \frac{\sqrt{3}}{2\sqrt{\pi}}\cos\theta |
| \psi_{21\pm1} | \frac{1}{2\sqrt{6}a_0^{3/2}}\frac{r}{a_0}e^{-\frac{r}{2a_0}} | \pm\frac{\sqrt{3}}{2\sqrt{2\pi}}\sin\theta e^{\pm i\phi} |
Here, we used the Bohr radius a_0 \equiv \frac{\hbar^2}{m_ee^2}\approx 52.9\,\mathrm{pm} as a convenient length scale. It can be seen from the table above that for higher principal quantum numbers, there are multiple states with the same energy. This degeneracy arises from the highly symmetrical form of the potential.
Moving beyond hydrogen complicates things significantly. No exact results exist, and perturbative calculations become extremely cumbersome, so numerical computation is the most feasible way forward. Conventional numerical studies of atomic and molecular structures are based on the variational method combined with a way to deal with the fermionic nature of electrons, such as the Hartree–Fock method. One should pick a set of basis functions to expand the eigenstates, and then minimize the energy over the coefficients of the expansion.
Hydrogen Atom in COMSOL Multiphysics®
In the case of the hydrogen atom, the TISE is simply a PDE for a complex-valued scalar field in 3D, thus allowing for a FEM-based solution of the eigenvalue problem. The Semiconductor Module, an add-on to COMSOL Multiphysics®, offers a Schrödinger Equation interface (also known as schr, as seen in the table below), which we can use for building our hydrogen atom model. The required settings are very simple.
We set up a sphere of radius A_0\equiv 15a_0, and in the Schrödinger Equation interface we modify the default nodes (Effective Mass and Electron Potential Energy) so that the effective mass is equal to m_e (in this model we do not have a periodic lattice) and the electron potential energy is equal to the Coulomb potential of the nucleus. The only boundary condition needed here is \psi \rightarrow 0 as r\rightarrow \infty, i.e., we are looking for bound states, so we surround the sphere with a thin layer and define it as an infinite element domain. To improve the computation speed, we use a mesh that becomes progressively coarser in the radial direction. Finally, we specify the energy scale as eV and estimate -15 eV as a starting point for the eigenvalue search.
The table below shows the eigenenergies obtained for the first two principal quantum numbers together with their theoretical values.
| n |
Analytical Method (-R_H/n^2 (\mathrm{eV})) |
COMSOL® (E_n(\mathrm{eV}) from schr) |
|---|---|---|
| 1 | -13.6057 | -13.6108 |
| 2 | -3.4014 | -3.4013 |
Note that the eigenvalues depend on the mesh used, so we always recommend running a mesh refinement study to get reliable results. To get an idea of the shape of the eigenstates, or orbitals, we plot them using 3D isosurface plots, shown in the figure below.

Orbital shapes of unperturbed hydrogen, visualized using a series of displaced 3D isosurface plots.
We adopt labeling used extensively in atomic physics: 1\mathrm{s}, 2\mathrm{s}, 2\mathrm{p}_x,\cdots. We can see that the s-states are radially symmetric, whereas each of the p-states has cylindrical symmetry along one of three mutually perpendicular axes. For s-states whose wavefunctions are spherically symmetric, the radial probability density has a simple analytical form that is defined as:
The comparison between the analytical results and simulated results are shown below.
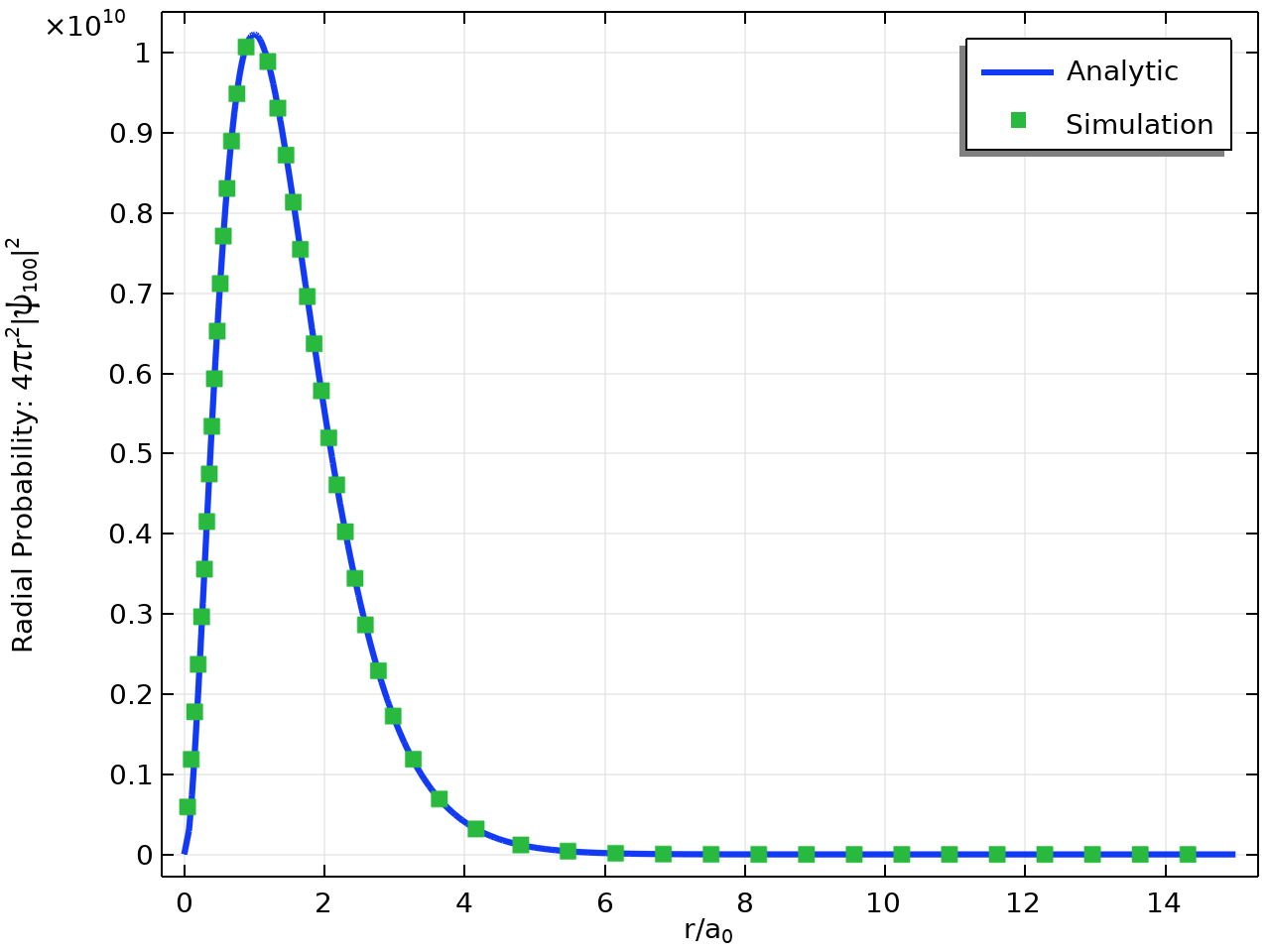
Radial probability of the 1\mathrm{s} state (ground state): the exact result (line) and the numerical result obtained using COMSOL® (points).
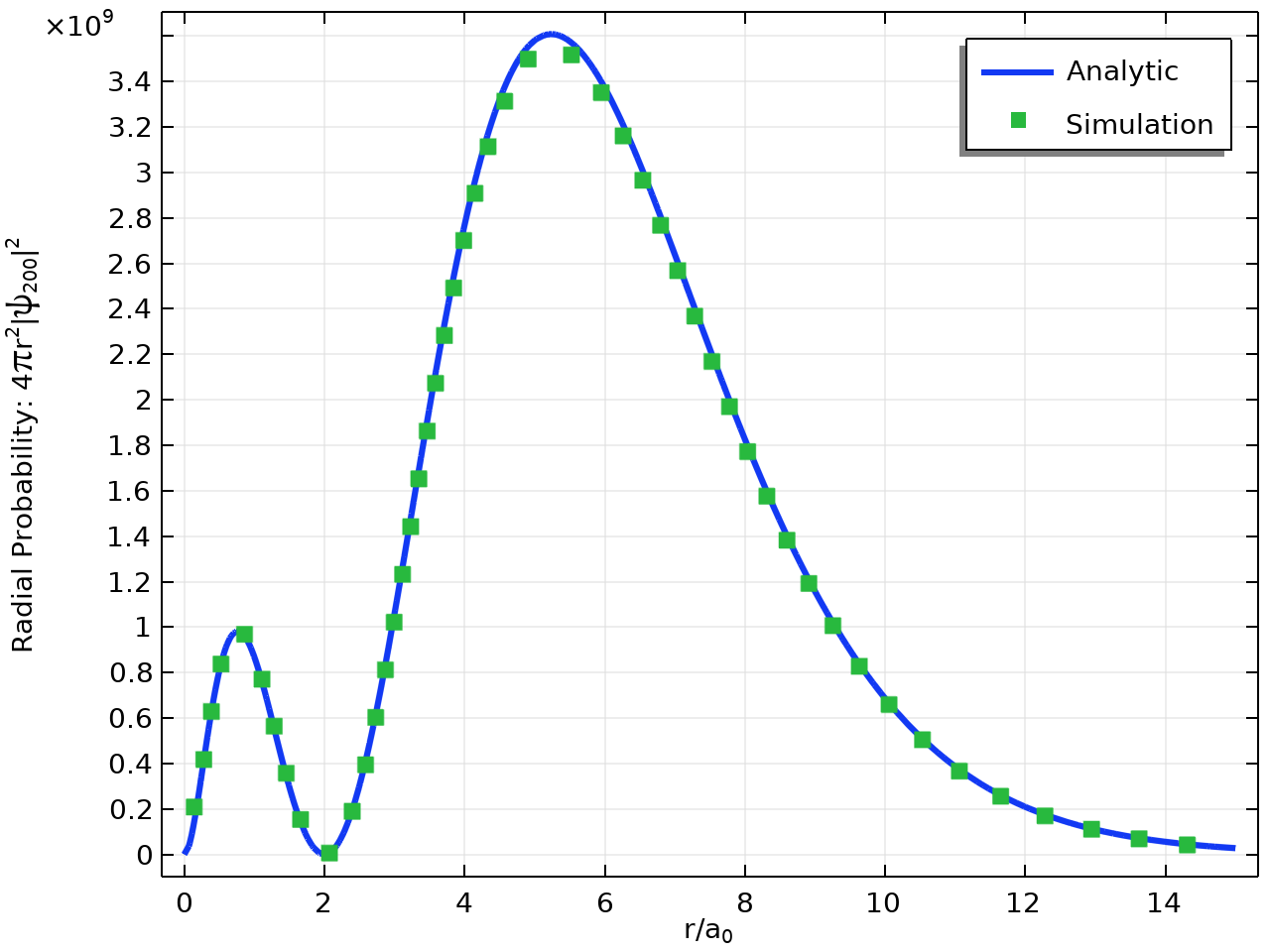
Radial probability of the 2\mathrm{s} state (first excited state): the exact result (line) and numerical result obtained using COMSOL® (points).
Stark Effect
An external electric field along, say, the z-axis, lifts some of the degeneracy we discussed earlier. The following term should be added to the Hamiltonian:
The resulting TISE can no longer be solved exactly, so we have to resort to perturbation theory. To the first order, the 1\mathrm{s}, 2\mathrm{p}_x, and 2\mathrm{p}_y states do not change in energy (or shape). However, the external field induces mixing between the 2\mathrm{s} and 2\mathrm{p}_z states, resulting in two split levels; this is an example of the Stark effect, and it can be observed experimentally in spectroscopic measurements. The corrections to the energy levels can be computed as follows:
On the other hand, finding the Stark splitting numerically with COMSOL® is just as easy as in the absence of an external field: if we simply add another Electron Potential Energy node to our model, we can readily obtain the split energy levels as well as the corresponding orbital shapes. To make the effect clearly visible, we used an extremely high external field of \sim2\times10^{8}\mathrm{V/m}.
| Split Energy Level | Perturbation Theory (eV) | COMSOL® (eV) |
|---|---|---|
| E_2+\Delta E_{\mathrm{Stark}} | -3.3714 | -3.3715 |
| E_2-\Delta E_{\mathrm{Stark}} | -3.4314 | -3.4315 |
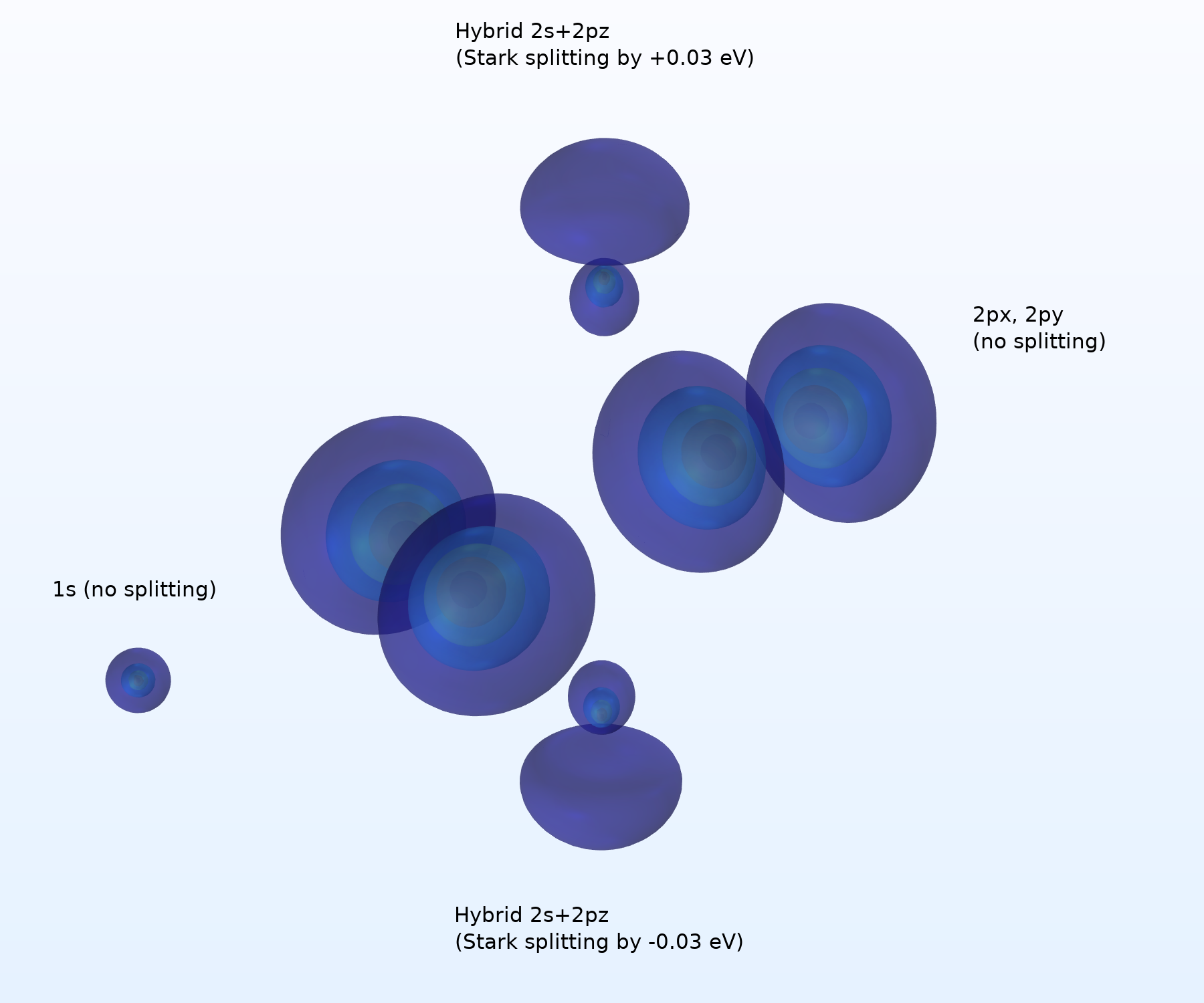
Orbital shapes in the presence of an external electric field along the z-axis.
Concluding Remarks
In this blog post we discussed some basics of quantum mechanics through the hydrogen atom and saw how to reproduce results using the Schrödinger Equation interface in COMSOL Multiphysics®. The model introduced here is not merely of pedagogical interest, however: It serves as a useful verification example of the software’s capabilities, and is of direct relevance to semiconductor physics where dopant states are often modeled using hydrogen-like wave functions. You can use this model and blog post as references for creating more accurate quantum mechanical simulations in COMSOL®.
If you’re interested in exploring the hydrogen atom further, download the example model discussed here by clicking the button below:
Further Learning
Learn more about quantum mechanics:




Comments (1)
Robert Koslover
May 12, 2023Nicely done. Thank you for providing this.