
You just got the latest smartphone, game console, or tablet. Eager to use it, you set it down to read the directions — but your child grabs it and starts shaking it around. The good news is that the device probably still works, as the internal electronic components have to be certified to function after experiencing certain shock loads. To analyze the shock response of an electronic part (like a circuit board), engineers can use numerical modeling.
The Impact of Mechanical Shock Testing
Many of today’s gadgets are becoming increasingly complex and mobile, and more of them are handhelds. As such, they’re more likely to sustain various loads and repeated impact, which means the more fragile components need to be tested before devices hit the market.

A laptop can undergo mechanical shock testing to ensure that the motherboard can withstand certain shock loads. Image by Ravenperch — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
Engineers use mechanical shock testing to gauge where a product is likely to take on damage from displacements, stresses, and impacts. Doing so helps them consider where to place more fragile components, like the motherboard, within the overall device so that they are better protected. Mechanical shock testing is often conducted in labs with equipment that performs half-sine, sawtooth, and trapezoidal pulses associated with impacts.
To save time and resources, engineers can analyze the shock response of fragile electronic components using simulation. Engineers interested in testing the shock response of consumer electronics can use the Structural Mechanics Module, an add-on to the COMSOL Multiphysics® software. In the next section, we detail two approaches for mechanical shock testing using COMSOL Multiphysics.
2 Approaches for Shock Response Testing
Is the Actual Shock Known?
Typically, for true shocks, the exact time history of the load isn’t known a priori. For example, if designing a building to withstand an earthquake, an engineer would study its peak response using a design response spectrum. By encompassing several different ground motions, they can estimate the peak response of the building when subjected to the as-yet-unknown earthquake.
However, when working with the certification of electronics, the exact shock, which the component must be able to withstand, is often prescribed. For example, a common shock specification is that the acceleration behaves as a half-sine function with a given period and peak amplitude. This makes true time-domain analysis a natural approach.
Time-Stepping Analysis
The most straightforward approach for simulating a shock is through a time-stepping analysis. If nonlinear behavior is to be taken into account, this is the only option. For a certification, however, we are more interested in whether or not the part breaks than how it breaks, so nonlinear effects may not be that important. In many cases, it is not necessary to perform a full nonlinear contact analysis, thus analyzing in a linear regime often makes sense. In particular, the mode superposition method is a computationally efficient method for linear dynamic analysis.
There is, however, one downside with time-stepping analysis: the amount of output data. Results must be stored for a large number of time steps, and all of these data must be scanned for worst cases during results presentation.
Response Spectrum Analysis
A response spectrum analysis is very lean on resources. The main computational effort is an eigenfrequency analysis. However, the final result — say, a peak stress or peak displacement — is only approximate. If, as in our example, the time history for the impact load is well defined, we can compute the corresponding response spectrum and use it as input for a response spectrum analysis.
In a response spectrum analysis, it is assumed that all support points experience the same acceleration history. This is typically true for a circuit board mounted inside a cabinet or chassis.
There are also plenty of examples in the aerospace equipment industry. During ground transportation, a component may receive a shock pulse if, say, a truck goes over a speed bump faster than it should. Transportation pulses are usually quite easy to replicate in a test lab; therefore, a time-stepping analysis would be appropriate. However, when the component is put into more complex designs like spacecraft, it needs to endure pyrotechnic shocks throughout the rocket motor ignition, staging, and deployment steps. These shocks often occur during satellite separation within the release mechanisms. It’s too difficult to represent pyrotechnic pulses through a time-domain function, so rather than trying to find an exact representation, a response spectrum is used to analyze a series of different pulses.
For our example, let’s investigate the effect of a half-sine shock load on a computer circuit board. Note that while using direct time stepping with mode superposition may be more appropriate for this example, we also compare it to a response spectrum analysis to demonstrate the two approaches.
Modeling the Shock Response of a Computer Circuit Board
For this example, let’s take a look at a motherboard design commonly used for smaller computing devices, such as game consoles. To set up the model geometry, the board can be set as a generic printed circuit board (PCB) material. Aluminum heat sinks cover a central processing unit (CPU) and a graphics processing unit (GPU) so that they keep cool. Silicon memory chips are placed next to the CPU, and cylindrical capacitors are scattered across the device. Along the edges are rectangular blocks representing plastic connectors for peripherals.
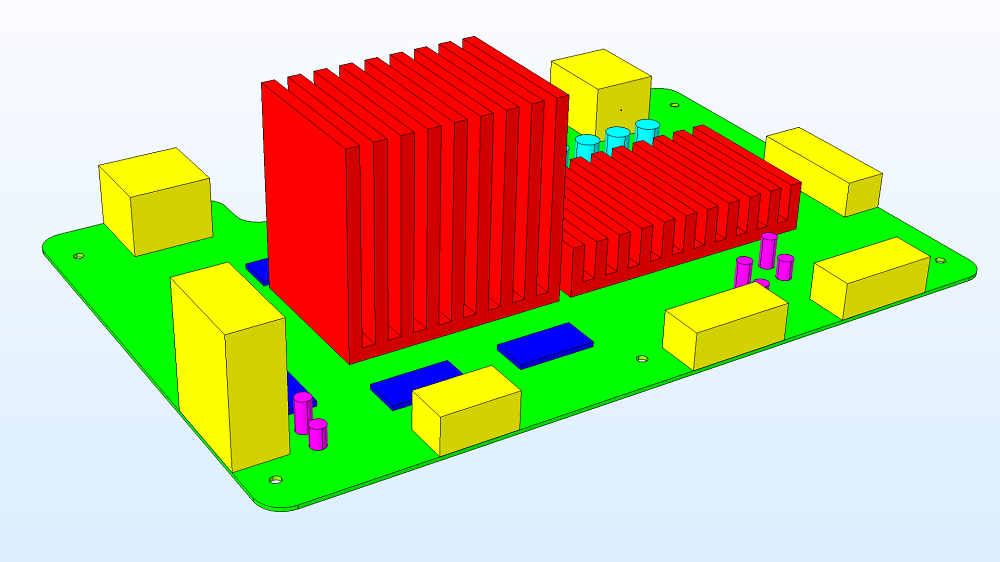
Motherboard geometry, including the PCB (green), heat sinks (red), memory chips (blue), capacitors (magenta and cyan), and plastic connectors (yellow).
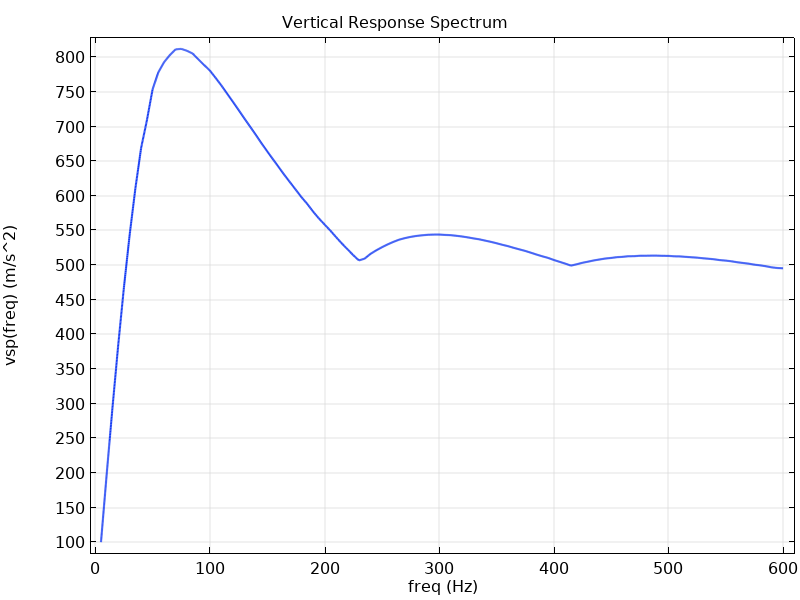
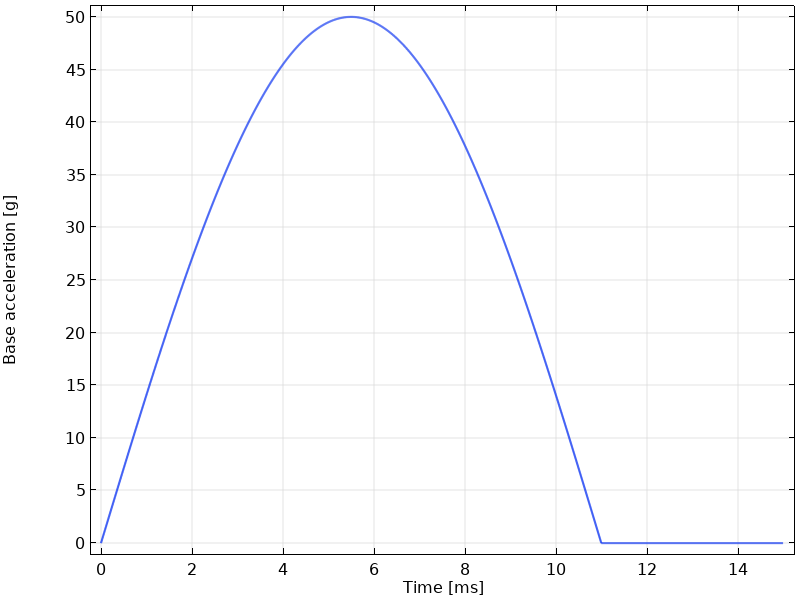
To set up the response spectrum analysis, the loading is represented by a pseudoacceleration spectrum, shown below. In this example, the pseudoacceleration spectrum corresponds to a pulse with a 50-g magnitude acceleration over an 11-ms duration.
Vertical spectrum (left) for a half-sine pulse with a 50-g shock load with an 11-ms duration (right).
Evaluating the Shock Response
Results for the Response Spectrum Analysis
Fundamentally, a response spectrum analysis relies on the different methods by which the eigenmodes of the structure are combined in order to estimate the total peak response. For the first step, you can perform an eigenfrequency analysis of the first 15 eigenfrequencies, examining their distribution together with the values of their participation factors. From the results, you can actually derive that these modes account for 94% of the vertical dynamic forces of the system. The graph below reveals that the first and third modes have the largest participation factor for vertical translation.
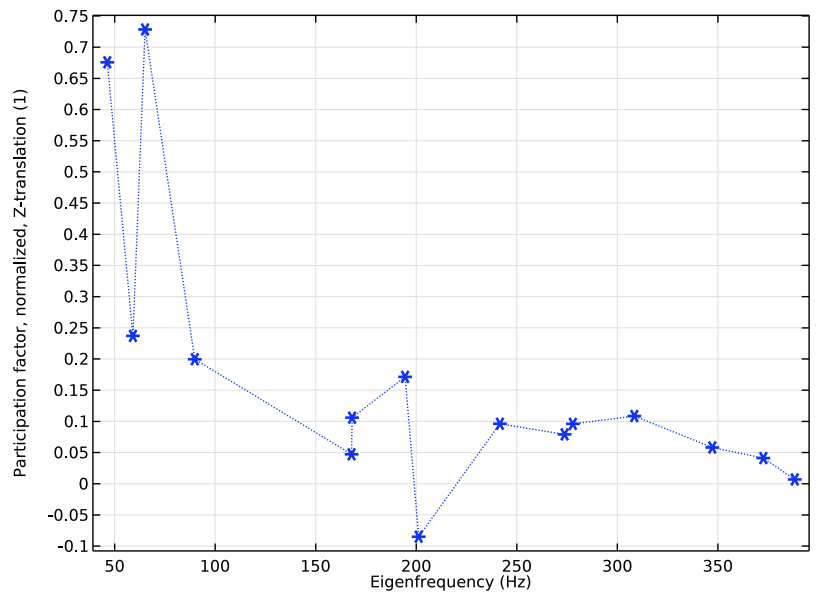
Participation factors for the eigenmodes corresponding to the first 15 eigenfrequencies.
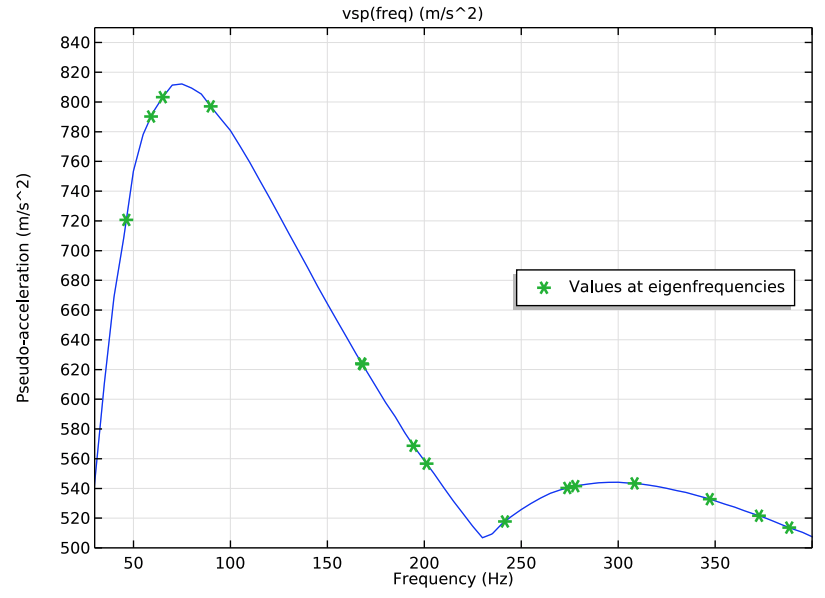
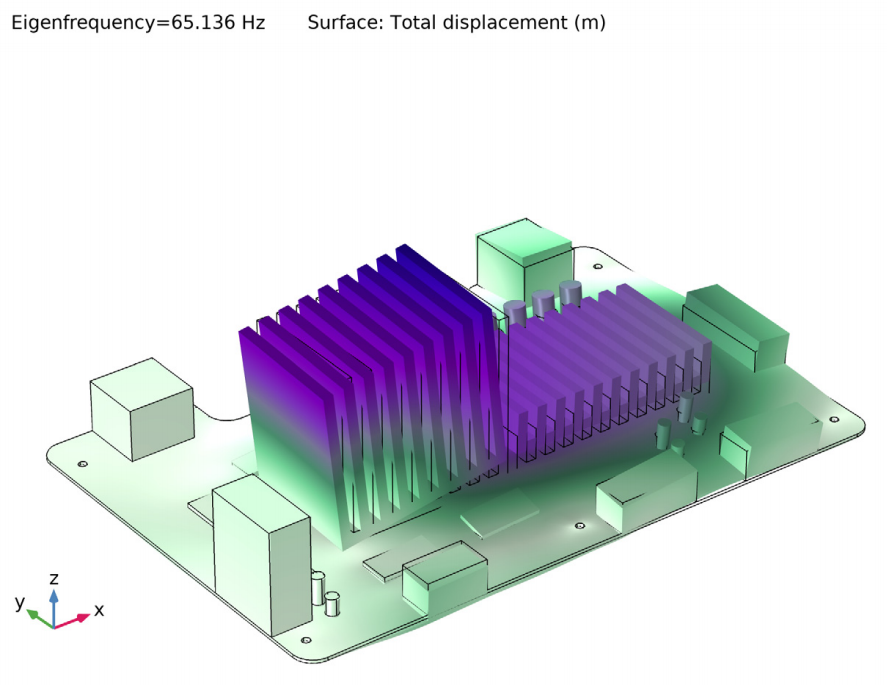
The next results show the values of the vertical shock spectrum computed at the eigenfrequencies. The eigenfrequency for the third mode is located close to the maximum of the input spectrum, indicating that this mode, together with the first mode, are the most important for the response. Actually, the product of the participation factor and the value of the response spectrum curve at the eigenfrequency provide the level of excitation for each eigenmode. So, in this case, we can assume that the first and third modes will be the major contributors to the dynamic response.
Left: Vertical shock spectrum input at the first 15 eigenfrequencies. Right: The third eigenmode.
Now that the eigenvalue solution is known, the response spectrum evaluation can be performed using a dedicated dataset called Response Spectrum. From the results, you can see the vertical displacement response (more on that in the next section) as well as the stress distribution (displayed below). For this design, the response spectrum analysis shows high stress levels near the memory chips.

Stresses in the motherboard.
Results for the Time-Stepping Analysis
For the time-stepping approach, you can perform the same analysis in the time domain using the Time Dependent, Modal solver. The first result of this analysis shows the vertical displacement of the system after 11 ms of transient loading at the end of the shock pulse.
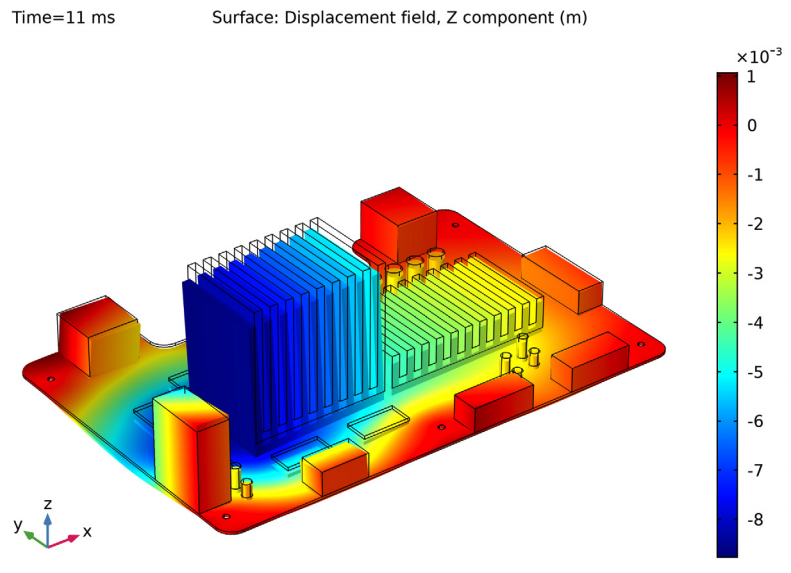
Dynamic response of the system at the end of the shock pulse.
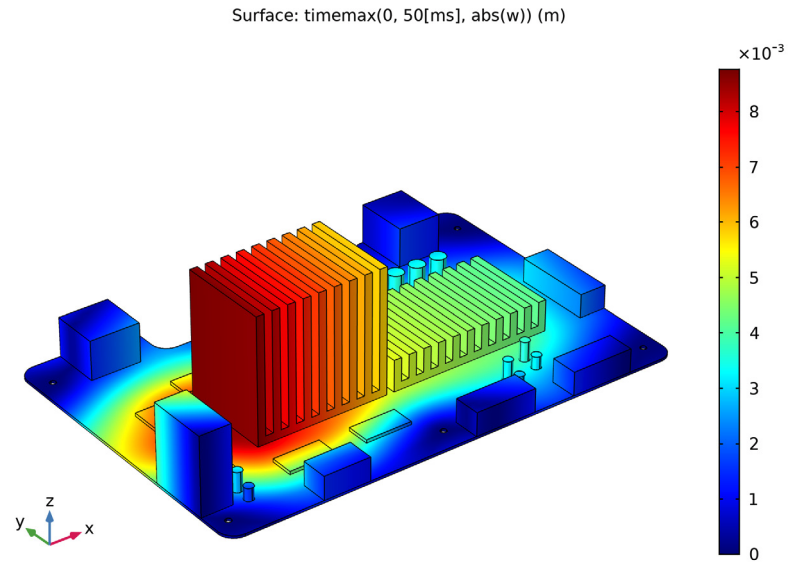
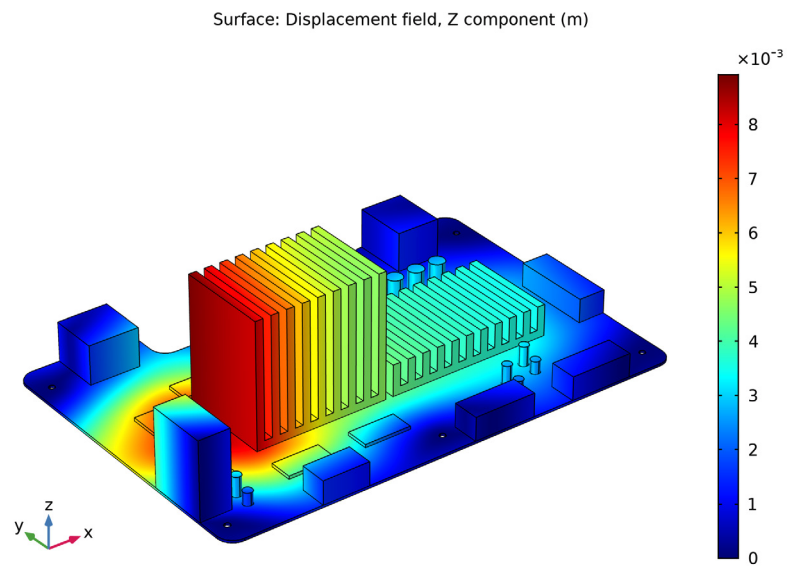
Next, you can see the maximum vertical displacement (below, left) computed over a 50-ms-long transient simulation. Note that this result gives the maximum deformation response for each point, even though the value could appear at different instances in time. Thus, it’s similar enough to the type of results that shock spectrum response computations provide that it can be compared to the vertical displacement results for the shock spectrum analysis from the section above (below, right).
Left: Maximum vertical displacement as determined by the time-stepping analysis. Right: Vertical displacement as determined by the response spectrum analysis.
The two shock response testing methods shown in this example each have their advantages, depending on the use case. The response spectrum method gives a less exact, approximate solution but can help with testing on a larger scale for more complex systems. The time-stepping method is more exact, but engineers must include a full solution for all of the time steps to find the maximum values when using this method, which causes a large memory consumption.
Next Steps
To try the Shock Response of a Motherboard tutorial, click the following button to go to the Application Gallery. There, you can take a look at the documentation for this example and download the MPH file.
Further Reading
Learn more about modeling electronic components:




Comments (2)
Christian Becker
March 27, 2020Hello!
How do I generate a pseudoacceleration spectrum?
Is there a calculation method to go from the half sine-puls to the vertical spectrum, or do I need to measure this data?
Regards Christian
Vincent Chung
August 6, 2021The simulation is clearly wrong… you have to know the eigenmodes prior to knowing the acceleration spectrum………So input the direct response diagram for simulation is wrong and pointless……It would be more useful to generate the response diagram from a modal analysis first……