While the mathematical study of chemical reactions has been performed for more than a century, it is only fairly recently that the computational tools for numeric integration of rate equations have been widely available. The old adage of “necessity is the mother of all invention” holds true in this instance. Here, you will find a classical analysis of a non-trivial reaction system, and learn how the simplified solution compares with the “real” one.
Lazy Molecules
The previous blog post introduced the concept of an activation energy. This is the required energy with which molecules must “impact” in order to react. For a great number of vital reactions, this energy is quite high. Some molecules, it turns out, are just lazy and quite content to stay in their present form. This is not necessarily a bad thing — take cattle, for example.
Cattle, like any organic matter, including humans, are inherently thermodynamically unstable; besides their water content, they consist largely of hydrocarbons, usually oxygenated and nitrated. This is a potentially combustible mixture that would be significantly more stable as carbon dioxide, nitrogen, and water. The thermodynamics would indicate that this is a much more energetically favorable form. Thankfully, the kinetics of their decomposition reactions are all quite slow — the molecules simply lack the activation energy necessary to decompose.
Now consider leaving a steak on a hot grill. If you do that, you’ll see what happens when activation energy is present in abundance; first, the meat will char, and eventually, you will be left with a pile of ash (the mineral, inorganic components of meat). This brings us to my next point: how do we humans gain energy from eating a (properly cooked) piece of meat? The answer is through catalysis.
Catalysts and Enzymes
A catalyst is a substance that somehow pulls and twists a molecule in such a way that it can react according to a different, energetically lower, pathway. The effect of this is that a reaction can suddenly proceed at an appreciable rate at much lower temperatures. Catalysis is everywhere — around 95% of all industrial chemical products go through at least one catalytic step in their lifetime.
One important group of catalysts, optimized over millions of years to work at very moderate temperatures, are enzymes. Enzymes are large molecules (usually consisting of several thousand atoms) that allow biological systems to perform the chemical reactions necessary to sustain life. Chew a piece of bread for a while and it will turn sweet — this is due to amylase, an enzyme present in human saliva that can turn starch into sugar to allow for easier digestion.
Pepsin
Moving back to our steak example, it turns out that the meat itself would be quite tough, unappetizing and difficult to digest if it weren’t for enzymes. Even before the beef hits our plate, the butcher will have hung the meat for several weeks to allow some of the naturally occurring enzymes to begin the process of protein degradation — thus tenderizing the meat and enhancing its overall flavor. Further down the line, the enzyme responsible for the degradation of protein in our digestive tract is called pepsin. Pepsin was in fact the very first enzyme to be discovered, so I feel it’s an apt example for this blog entry. Let’s take a closer look at how pepsin works.
In an initial step, the substrate S (in this case the beef protein) must associate with the enzyme E.
E + S → ES
This substrate-enzyme complex ES can just as well separate again into the substrate and the enzyme according to:
ES → E + S
The two reactions are usually written as one, using a shorthand description for reversible reactions as:
E + S ↔ ES
Instead of dissociating, the substrate may react while complexed to the enzyme. The enzyme then releases the product protein:
ES → E + P
The entire system may thus be written as:
E + S ↔ ES → E + P
This reaction is closely related to the example in the previous blog post on chemistry. Let us now attempt to formulate the rate equations for this system.
Michaelis-Menten Kinetics
The production of the substrate-enzyme complex ES is:
(1)
And its consumption:
(2)
We now assume the so-called (pseudo-)steady state approximation (PSSA or SSA) for ES. This common approximation suggests that a reactive intermediate like the enzyme-substrate complex is highly reactive. The reactions that consume the product species — dissociation or reaction — are assumed to be inherently fast compared to complex formation. In this case we can approximate that the rate of change of the concentration of ES is negligible. We are allowed to do this even though the concentration of ES may change as the reaction proceeds; what matters is that on the time-scale of the reaction we are interested in, the concentration of ES responds very quickly to a change in the overall concentration of the reactant substrate S.
This approximation leads to:
(3)
which is equivalent to:
(4)
Collecting all the terms on the left and lumping them into a Michaelis-Menten equilibrium constant K_\mathrm{M}, we obtain
(5)
Regarding the concentration of the enzyme present in the system, we know the initial concentration of E, and we already have defined a variable for ES, so we can write:
(6)
Inserting this into the above and solving for the concentration of ES, we are left with:
(7)
This result can be used to determine the production rate of the protein:
(8)
It is interesting to note here that under conditions of high substrate concentration (as is usually the case when the reaction has not yet proceeded far), we can approximate that c_\mathrm{S} \gg K_\mathrm{M}. Under these conditions:
(9)
Under these conditions, the rate of substrate consumption is independent of the substrate concentration itself: it is “zeroth order”. The rate only depends on the available concentration of the enzyme, which catalyzes the substrate reaction as fast as it can. The quantities K_\mathrm{M} and v_\mathrm{max} together are used to define the kinetics of the reacting system.
This whole derivation is known as the Michaelis-Menten mechanism, named after Leonor Michaelis and Maud Menten. It finds wide application in a plethora of biochemical reactions. At the time Michaelis and Menten published their results 101 years ago, they had no access to a digital computer with which to quickly integrate the system of differential equations for the four species. Instead, by performing the above analysis with an intuitive, physically motivated approximation, they obtained a simple relationship that showed them what influence the enzyme and substrate concentrations had on the rate of enzymatic reaction. How good is this approximation? Thankfully, we can now calculate the full model — without the PSSA for ES — and compare it with the result for the simplified equation.
Enzyme Kinetics in COMSOL
Using the Reaction Engineering interface, typing in the two relevant reactions is simple and intuitive. By using the <=> symbols, COMSOL Multiphysics immediately understands that a reversible reaction is to be simulated, enabling the necessary input fields for both forward and reverse rate constants (as well as generating variables for E, S, and ES). In the same manner, once the equation for the production of P has been typed in, a variable for the corresponding concentration is created.
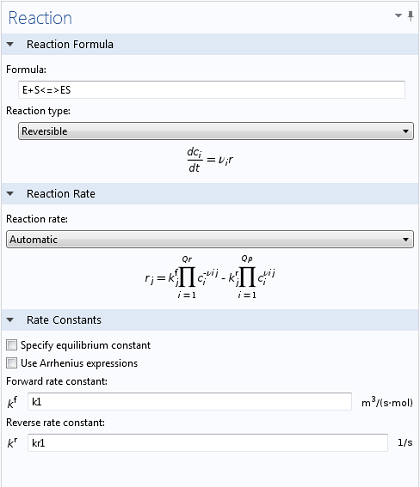
Values of k1 = 1700 M-1 s-1, k-1 = 10-3 s-1, and kcat = 0.5 s-1, as well as reasonable values for the initial concentrations of E and S, were taken from literature (Calorimetric Observation of a GroEL-Protein Binding Reaction with Little Contribution of Hydrophobic Interaction; K. Aoki et al. J Biol. Chem. vol. 272, pp. 32158-32162, 1997). As we are dealing with such significant differences in scales, the two highly concentrated species (P and S, Figure 1) are shown separately from the highly dilute species (E and ES, Figure 2). Note that this difference in scales inherently justifies our use of a steady state approximation!
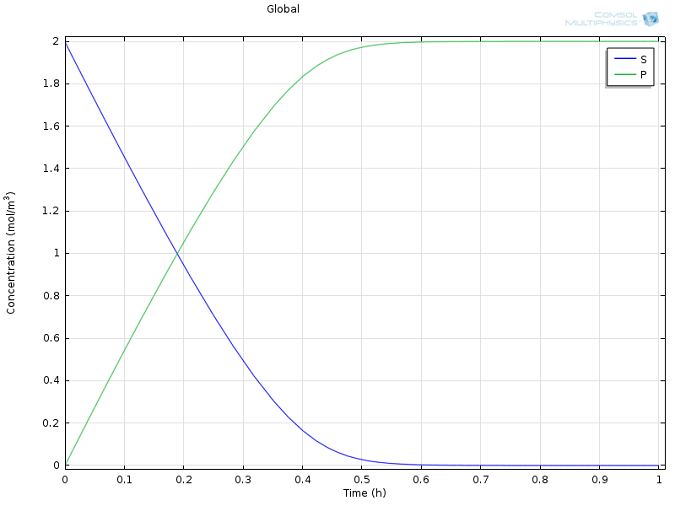
Figure 1: Concentration profiles of substrate (blue) and product (green) over time.
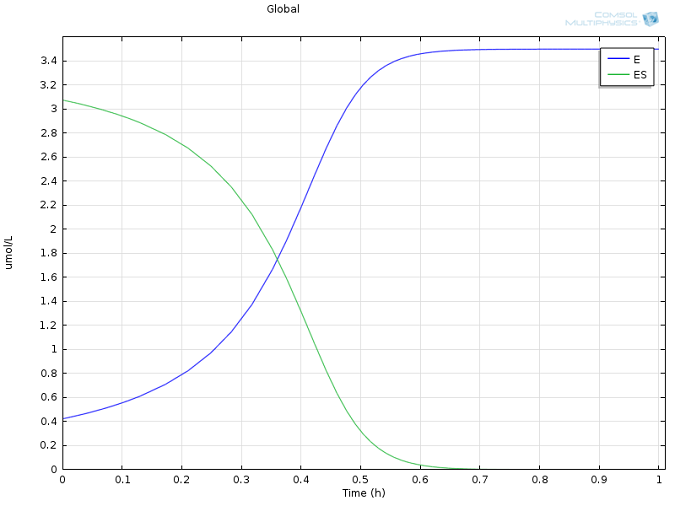
Figure 2: Concentration of enzyme (blue) and enzyme-substrate complex (green) over time.
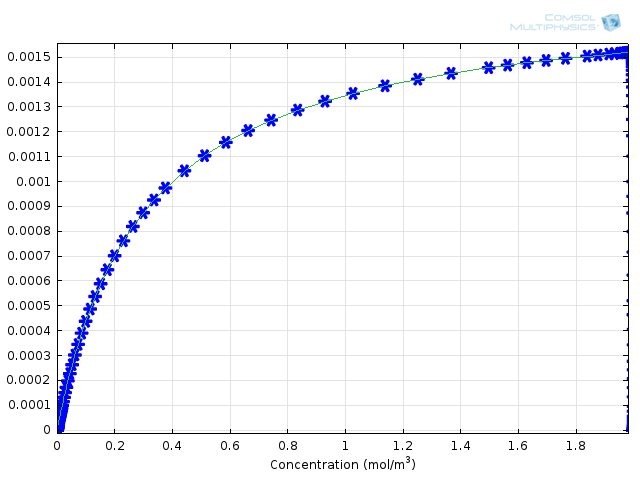
Figure 3: Comparison of Michaelis-Menten kinetics (green solid line) with fully integrated reaction mechanism (blue asterisks).
Concluding Remarks and Next Steps
How can these results give us an idea of the error associated with the Michaelis-Menten mechanism? We can compare the results with the calculated formula for the rate of formation of product. To do this, the COMSOL variable comp1.re.r_2, the rate for the production of protein, and kcat*E0*comp1.re.c_S/(Km+comp1.re.c_S), the derived Michaelis-Menten expression, are plotted on the same 1D Plot Group as functions of substrate concentration. This yields Figure 3, above. You can see that the agreement is very good between the approximate theory and the complete numerical approach.
Just after the 100-year anniversary of the Michaelis-Menten mechanism, we honor their trailblazing publication the best way we know how — by simulating.



Comments (1)
John Aggas
March 25, 2024Is it possible for you to upload the example file used in this blog post?