
Whenever modeling magnetic fields in steady-state, transient, or frequency domain with the AC/DC Module, we want to reduce the size of the model as much as possible to minimize the computational resources and time needed to solve the model. Today, we will introduce symmetry boundary conditions that you can exploit in your modeling and show how to use them.
Modeling a Coil with Three Symmetry Planes
First, let us look at a rectangular wound multi-turn coil, as shown in the figure below. A spherical modeling domain contains a rectangular coil. The coil domain represents several hundred turns of wire wrapped around a rectangular profile. The lead wires that excite the coil are neglected from the model, and we treat the coil as a closed loop of current. The Multi-turn coil feature is used to compute and apply a uniform current distribution around the profile of the coil, and the steady-state magnetic field is plotted. Note that the coil domain has a constant cross-sectional area as we follow the path of the current around it.
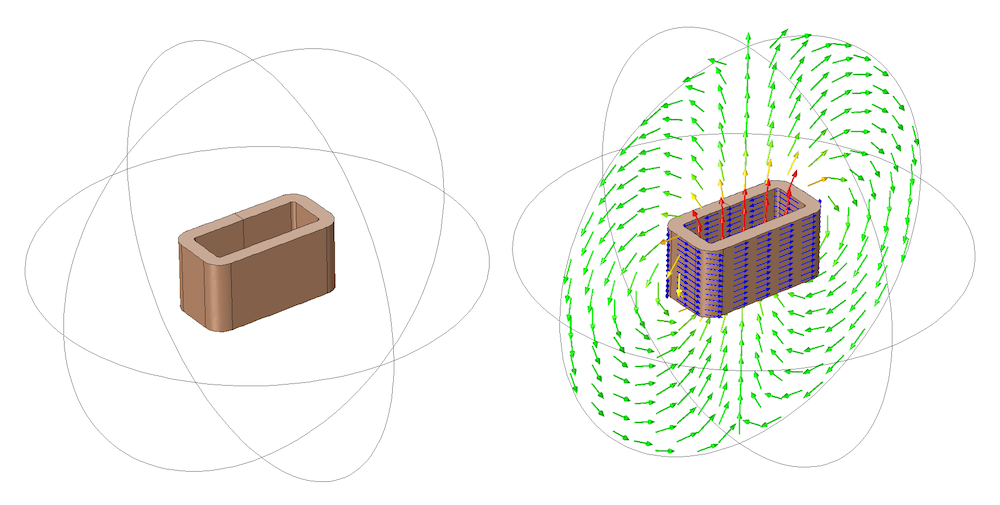
A rectangular coil with current flowing around the winding direction. Current flow (blue arrows) and magnetic field are plotted.
This modeling domain has three planes of symmetry, i.e. planes about which the geometry is exactly mirrored. Let us now see how we can use this geometric symmetry as well as our knowledge of the magnetic field and what direction the current is flowing to reduce the size of our modeling domain.
The Magnetic Insulation Boundary Condition
The Magnetic Insulation boundary condition represents a mirror symmetry plane for the magnetic field. The magnetic field will be exactly mirrored as you cross the plane.
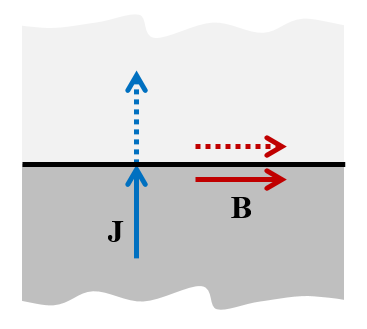
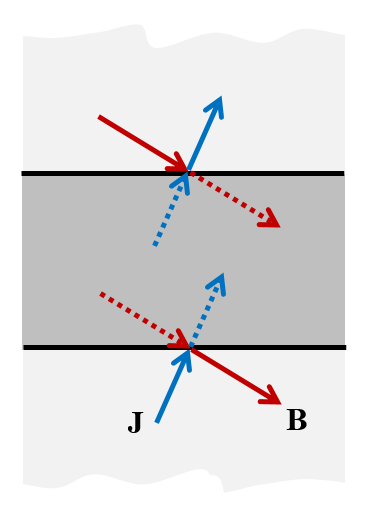
The Magnetic Insulation boundary condition — “cut perpendicular to J and parallel to B“.
This boundary condition also means that the magnetic field is zero in the normal direction to the boundary. That is, the magnetic field must be tangential to this boundary. As a consequence, this boundary condition has the physical interpretation of a boundary through which current can only flow in the normal direction. The modeling rule can be summarized: “Use Magnetic Insulation to cut perpendicular to J and parallel to B.”
The Perfect Magnetic Conductor Boundary Condition
The Perfect Magnetic Conductor boundary condition, on the other hand, represents a mirror symmetry plane for the current. From a mathematical point of view, it can be thought of as the “opposite” of the Magnetic Insulation boundary condition.
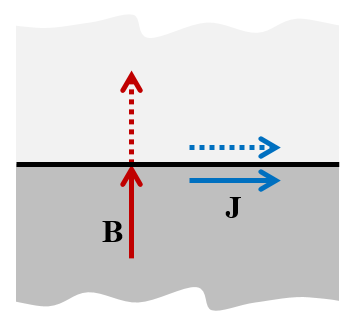
The Perfect Magnetic Conductor boundary condition — “cut perpendicular to B and parallel to J“.
The current vector will be exactly mirrored as you cross the plane and can have no normal component, so the current must flow tangentially. This boundary condition enforces that the magnetic field can have no tangential component as you approach the boundary, so the magnetic field can only point in the normal direction and cannot change sign as you cross the boundary. The modeling rule can be summarized: “Use Perfect Magnetic Conductor to cut perpendicular to B and parallel to J.”
The Simplified Coil Model
The original geometry can be reduced in size to a one-eighth model representing the original geometry. Orthogonal planes through the center of the coil are used to partition the domains as shown below.
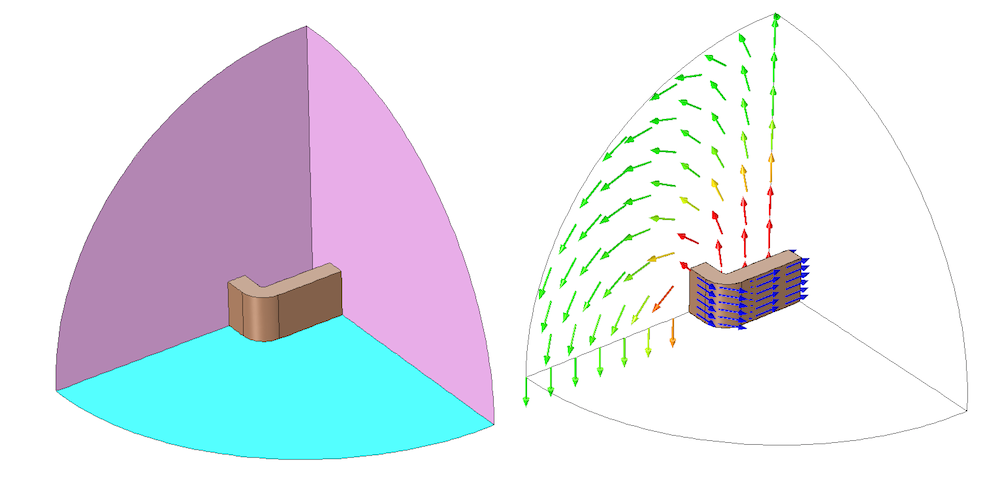
A one-eighth symmetry model of a rectangular coil with current flowing around the winding direction. The Magnetic Insulation (magenta) and Perfect Magnetic Conductor (cyan) boundary conditions are applied along the appropriate symmetry planes for this problem.
The Magnetic Insulation boundary condition is applied at the two boundaries representing the planes through which the current will flow normally. If the coil is excited with a voltage boundary condition, it is important to reduce the voltage by a factor of two for each Magnetic Insulation symmetry condition applied. If the coil is excited with current, the applied current does not need to be changed, but the postprocessed coil voltage should be scaled by a factor of two for each Magnetic Insulation symmetry condition.
The Perfect Magnetic Conductor condition is used at the plane along which the current will flow tangentially. Since the Perfect Magnetic Conductor condition cuts the coil in half, it is important to divide the applied current in half when a current excitation is used. On the other hand, if a voltage excitation is used, then the postprocessed coil current must be scaled up by a factor of two for each Perfect Magnetic Conductor symmetry plane.
The Periodic (Boundary) Condition
In almost all cases, the Magnetic Insulation and Perfect Magnetic Conductor boundary conditions are sufficient to significantly reduce the size of your model. As we saw earlier, these conditions enforce the current and magnetic fields to be either normal or tangential to the boundary. But what if we have a geometric symmetry plane where the fields do not have such a symmetry? In such cases, the Periodic (boundary) condition may be appropriate.
The Periodic condition is used when all we know is that the solution must be periodic.
The Periodic (boundary) condition allows for more general symmetry where both the current and the magnetic field vector can be at an angle to the boundary. The usage of this condition is limited to cases where the magnetic sources as well as the structure are periodic in space. Typically, the full geometry can be reduced to the smallest repetitive element, a unit cell, limited by periodic conditions.
Consider the structure of a toroidal inductor wound with a single strand of wire, shown below. The wire can be modeled fairly accurately as a single continuous spiral around the toroid, as long as we again neglect the asymmetry due to the lead wires. We can model the wire as an edge current, flowing tangentially to the wires.
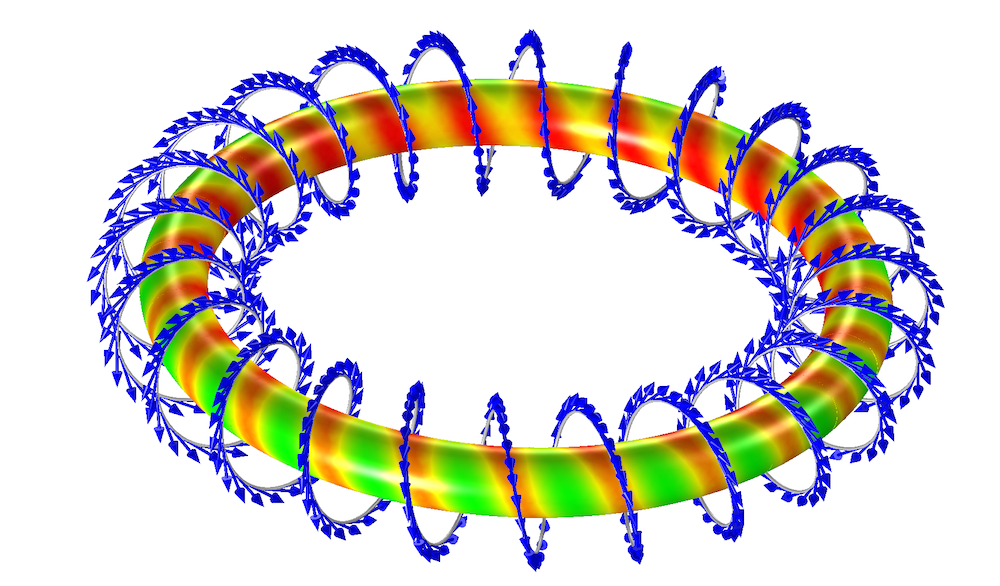
A spirally wound toroidal inductor. The arrows (blue) indicate the direction of current flow. The magnetic field in the core is shown.
To exploit as much symmetry as possible here, we can consider the unit cell that is just a small slice of the original model containing a single turn of the winding. The Periodic condition is used along the sides of the slice. When using this boundary condition, the mesh must be identical on the periodic faces, so the Copy Face functionality should be used to ensure identical meshes. As we can see from the image below, the size of the model can be reduced by the number of windings, greatly reducing the problem size.
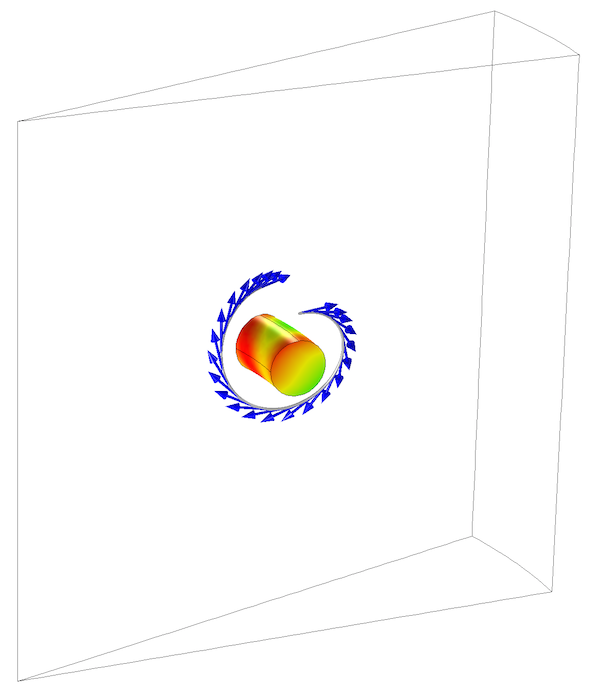
Periodic conditions can greatly reduce the model size for certain geometries.
The generality of the Periodic condition comes at a price compared to the more basic Magnetic Insulation and Perfect Magnetic Conductor conditions. As it links the unknown fields on one side of the geometry to those on the opposite side, it makes the system matrix more dense and expensive to solve. Therefore, do not use it if the more basic conditions apply.
The Symmetry Plane Boundary Condition
In version 6.0, we introduced a new Symmetry Plane boundary condition (shown below). This feature imposes either a Symmetry condition to the magnetic flux density, which is equivalent to the aforementioned Magnetic Insulation boundary condition, or an Antisymmetry condition, which is equivalent to the Perfect Magnetic Conductor boundary condition. This new feature can be used instead to simplify model setup.
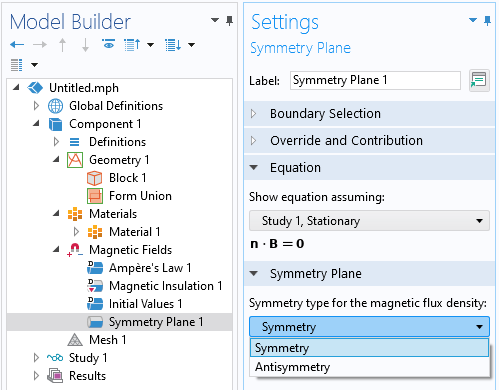
Screenshot of the new Symmetry Plane boundary condition
Summary of Exploiting Symmetry When Modeling Magnetic Fields
By reducing the model size, we also reduce the computational requirements significantly. In fact, computational requirements grow exponentially with problem size, so the more symmetries that we can use, the better. Even if you don’t have symmetry in the full problem that you want to solve, it is often advisable to work with a smaller model that does have symmetry in the initial developmental stages of your modeling.
Next Step
Want to learn more about symmetry boundary conditions? Contact us via the button below:
Further Resources
- If you would like to practice your simulation skills, you can check out these related tutorial models:
Editor’s note: This blog post was updated on August 31, 2022, to include discussion of a new feature available as of the COMSOL Multiphysics® software version 6.0.




Comments (15)
Ryan
October 10, 2014Walter, this post motivated me to explore periodic boundary conditions. Do you have a model of the toroidal inductor that I can download?
Thanks,
Ryan Clary
Fanny Griesmer
October 14, 2014 COMSOL EmployeeHello Ryan,
Although we don’t have a full example model of this situation (yet), please contact COMSOL Support and we can make a sample file available for you.
Best,
Fanny
nde
April 1, 2015Hi,
Thanks for the great article. I was wondering how these boundary conditions can be expressed in terms of magnetic vector potential.
From what I have gathered, the Perfect Magnetic Conductor boundary condition corresponds to a Zero Neumann boundary condition, where the normal derivative of the magnetic vector potential is set to zero at the boundary:
n ⋅ ∂A/∂r = 0
From the above, how can one prove that this forces the magnetic flux density vector to cut the boundary at right angle?
Also, I am having trouble figuring out what the Magnetic Insulation boundary condition corresponds to. Is it a Dirichlet boundary condition?
If yes, is it n ⋅ A = 0, or just A = 0 ?
If it is the former, I can see how the magnetic flux density is zero in the normal direction to the boundary and non-zero in the tangential direction.
Thanks in advance for your time.
Walter Frei
April 1, 2015 COMSOL EmployeeDear O Kyp,
These are indeed some very interesting questions, I would suggest a textbook on computational electromagnetics if you’re interested in an extensive discussion about how these conditions are formulated. The COMSOL documentation and the equation view will also show you what equations COMSOL is implementing.
Simon Mariager
November 12, 2015Dear Walter Frei
Thank you for a very nice and clearly written blog post. One question. Is there a way to implement the perfect magnetic conductor boundary condition with the magnetic fields no currents physics? (Comsol 5.1)
I am trying to solve a problem involving permanent magnet and would like to take advantage of all symmetry planes, but this boundary condition seems to be available only for the other ACDC physics.
Thank you,
Simon
Walter Frei
November 13, 2015 COMSOL EmployeeDear Simon,
For symmetry in the Magnetic Fields, No Currents formulation you would have the Magnetic Insulation and the Zero Magnetic Scalar Potential boundary conditions. Please see, for example:
http://www.comsol.com/model/permanent-magnet-78
Hamed Ahmadpanahi
June 15, 2016Dear Walter,
Thanks for a very clear explanation of these boundary conditions.
Is there any way to combine Periodic condition with symmetry boundary condition in RF module?
For an example, imagine that instead of one coil, there is an array of coils and we would like to see the Magnetic field. Using Magnetic Insulation and Perfect Magnetic Conductor boundary condition we can calculate the field for only one coil while we know that the field is periodic.
Is there any example that uses Periodic boundary condition with Perfect Magnetic/Electric Conductor ?
In the application library i was not able to find any. There are many examples on periodic boundary conditions (Modeling of Pyramidal Absorbers, Frequency selective surface, hexagonal grating…) but in none of them the electric/magnetic field symmetry has been considered.
Would you please let me know if there is any documents or example ?
Best regards
Hamed
Walter Frei
June 17, 2016 COMSOL EmployeeDear Hamed,
It is not quite clear what you meant here by combining the periodic condition with the symmetry condition. I believe that, for what you’re describing, a set of periodic coils stacked in parallel, you could simply use the PMC condition on the symmetry plane.
Best Regards
Wajid Ali
June 4, 2017Hello,
My question is slightly irrelevant but I am facing great difficulty in how to apply a constant Magnetic field of 1.5 T along the propagation of light while finding the absorption cross section of gold nano sphere in RF module.
My aim is to find the effect of Magnetic field on absorption.
Yours suggestion will be greatly appreciated…….
Ali
Wajid Ali
June 4, 2017Hello,
My question is slightly irrelevant but I am facing great problem that how to apply constant magnetic field of 1.5 T along with the direction of propagation of light while finding the absorption cross section of gold nano sphere .
Your response will be greatly appreciated .
Regards
Ali
wakhanqau@yahoo.com
Caty Fairclough
June 21, 2017Hi Wajid,
Thanks for your comment.
For your question, please contact our Support team.
Online Support Center: https://www.comsol.com/support
Email: support@comsol.com
Xiruo Yan
April 4, 2018Hello,
Fascinating blog article, very intuitive! It worked well for my EM resonator problem. However, can I ask a question about the result visualization?
Utilizing the symmetry, only part of the whole structure needs to be constructed, but also only that part will be simulated and have data. Is there a way to map (eg. electric field mode profile of) the simulated region to those unconstructed region and get a full plot (of overall mode profile)?
Thank you.
Best,
Xiruo
Walter Frei
April 5, 2018 COMSOL EmployeeHello Xiruo,
There are Mirror operations within the Results > Data Sets branch that will allow you to visualize the total solution.
Best Regards,
Benozir Ahmed
June 20, 2018Dear Walter,
Thanks for the article. I have a question which is not quite relevant though. While working with Magnetic Field(MF) physics, if I scale down the geometry (Geometry>Length Unit> cm) to millimeter or micrometer then the solver fails to solve. Even I downloaded some running models from COMSOL website and scaled down the geometry to centimeter and those models also suffers can’t solve. Do you know any solution to the problem? I will appreciate any suggestion.
Suzanne Ashcraft
July 9, 2018I’m having trouble getting my solenoid inductor to run in ACDC module, its just taking forever to compute or won’t compute. By more expensive what did you mean by that? I was trying to decide if this was worth trying.
The generality of the Periodic Condition comes at a price compared to the more basic Magnetic Insulation and Perfect Magnetic Conductor conditions. As it links the unknown fields on one side of the geometry to those on the opposite side, it makes the system matrix more dense and expensive to solve. Therefore, do not use it if the more basic conditions apply.