In the previous blog post, What Is Gauge Fixing? A Theoretical Introduction, we gave a theoretical background to gauge fixing; that is, why and when it is required. Here, we continue to discuss its implementation and how to use it in the context of the COMSOL Multiphysics® software.
The Short Guide to Gauge Fixing: Generally Not Necessary
In our previous blog post, we introduced three potentials that are used to formulate some of the physics interfaces in the AC/DC Module; i.e., the electric scalar potential V, the magnetic scalar potential V_m, and the magnetic vector potential \textbf{A}.
We have shown that unless reference levels for V and V_m are defined and \nabla \cdot \textbf{A} is specified, the potentials are not uniquely determined. When the solution is not unique, the numerical problem to be solved is singular. In that case, COMSOL Multiphysics defaults to using an iterative solver that will converge to a solution; which one does not matter as all yield the same physical fields (\textbf{E}, \textbf{D}, \textbf{H}, or \textbf{B} — depending on context).
Check out this Knowledge Base entry to understand the difference between the iterative and direct solvers.
In the AC/DC Module, an add-on to COMSOL Multiphysics, there are three physics interfaces that solve for the \textbf{A} field:
- Magnetic Fields (mf), which is based on the \textbf{A} formulation and where \textbf{A} is the only dependent variable. In statics, this solution is not unique without gauge fixing, whereas in dynamics, additional terms of inductive origin make the solution unique, provided those terms are numerically significant.
- Magnetic and Electric Fields (mef), which solves the fully coupled \textbf{A} and V fields. Due to the gauge transformation, there is no unique solution unless \nabla \cdot \textbf{A} is specified.
- Rotating Machinery, Magnetic (rmm), a combination of the \textbf{A} formulation and V_m formulation. The \textbf{A} formulation is used to model conductive (current-carrying) domains, and the V_m formulation is used for the air gap and other nonconducting domains. The two formulations are coupled on their common interfacing boundaries. Since the rmm interface is a mixed formulation, the comments on gauge fixing for the Magnetic Fields (mf) interface apply.
As a summary, the table below lists the properties of the solution and required numerical solver for the mf, mef, and rmm interfaces and for different study types without gauge fixing. Due to the default iterative solvers for these three interfaces, gauge fixing is generally not necessary.
| Interface, Attribute | Stationary | Time Dependent, \sigma=0 | Time Dependent, \sigma>0 | Frequency Domain, \omega>0 |
|---|---|---|---|---|
|
mf, rmm Solution |
Nonunique | Nonunique | Unique | Unique |
|
mf, rmm Solver |
Iterative only | Iterative only | Iterative or direct | Iterative or direct |
|
mef Solution |
Nonunique | Covered by the usage of the mf interface | Covered by the usage of the mf interface | Nonunique |
|
mef Solver |
Iterative only | Covered by the usage of the mf interface | Covered by the usage of the mf interface | Iterative only |
It is worth mentioning that even in the case when the potentials lack unique solutions, the physical fields \textbf{E} and \textbf{B} are always unique. The potentials are not directly measurable and have no direct physical meaning, so for the potentials, any solution fulfilling the equations will do.
As an illustration, take the Inductance of a Power Inductor model available in the Application Library. The model is built with the mef interface and solved in the frequency domain; first without gauge fixing and then with gauge fixing.
As shown in the figure below, the V field differs significantly, while the norm of the \textbf{E} field is invariant as expected. The top-right figure shows a V field that varies smoothly in the domain when gauge fixing is applied. This is quite different from the field without gauge fixing, as shown in the top-left figure. It is interesting to notice that we call this gauge (\nabla \cdot \textbf{A} = 0) the “Coulomb gauge” because it enforces a V field that behaves like the Coulomb potential, which results from a static electric charge density. As the physical fields \textbf{E} and \textbf{B} are the same, the computed reactance values also agree.
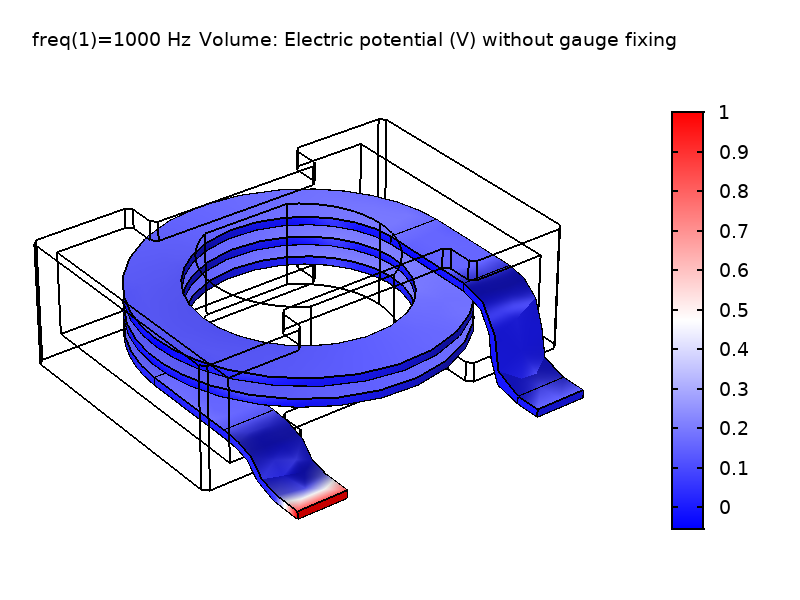
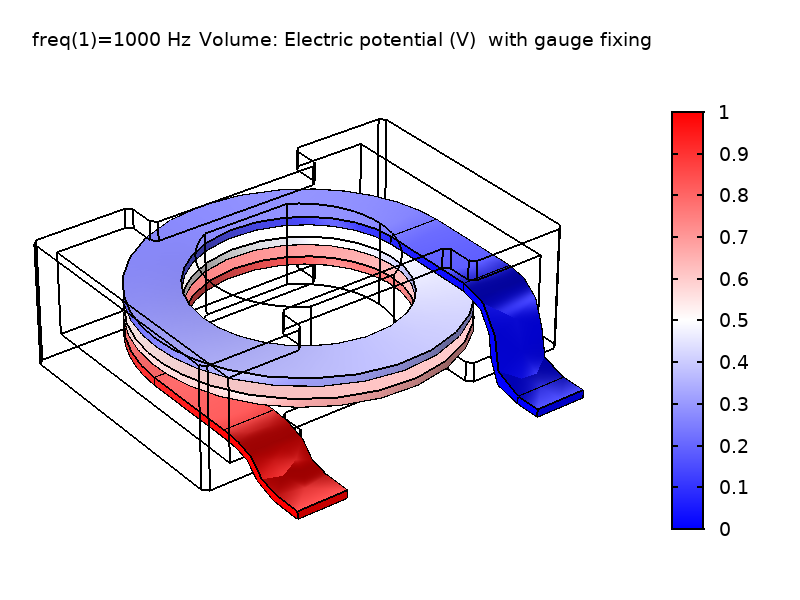
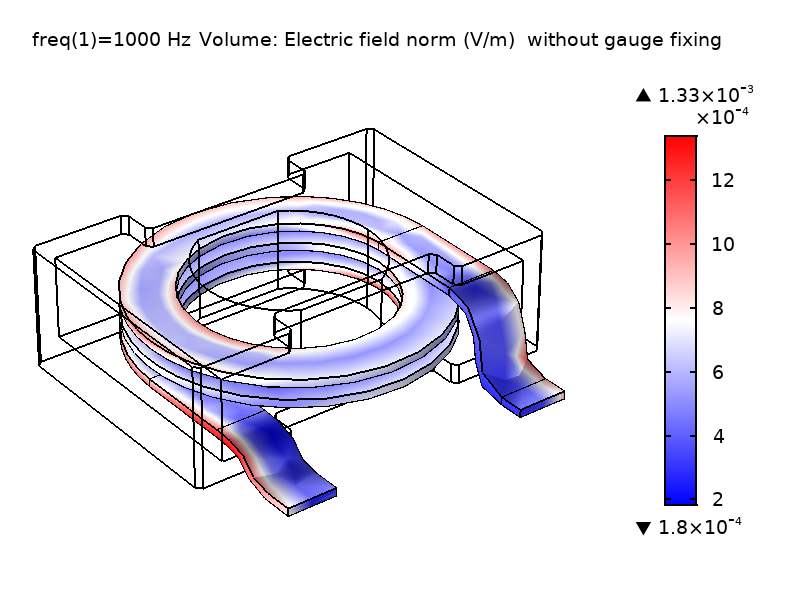
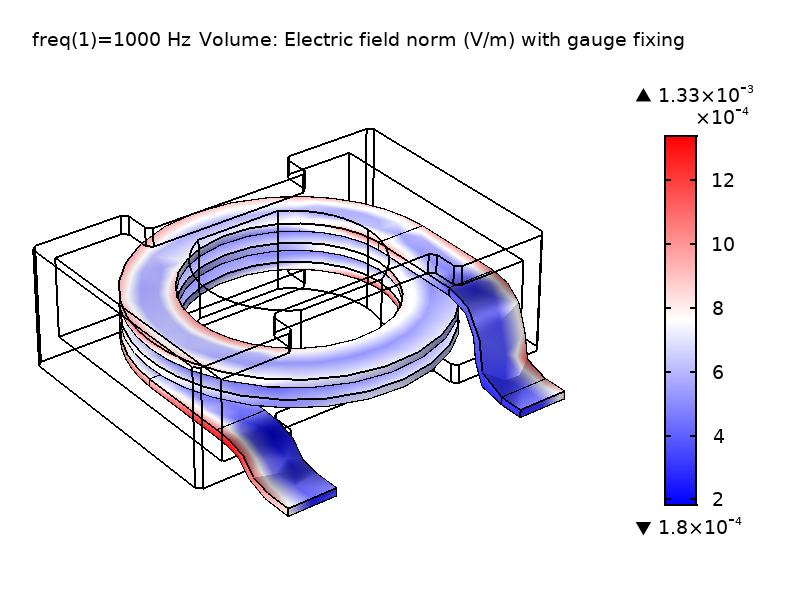
Figure 1: Comparison of the computed V field and \textbf{E} field norm in the coil domain solved without gauge fixing (left) and with gauge fixing (right).
Gauge Fixing in the AC/DC Module
Gauge fixing is usually required when the solution of the \textbf{A} field is not unique and you want to use a direct solver. Using a direct solver may be required or beneficial in cases involving multiphysics couplings, as iterative solvers and preconditioners typically are tuned for one specific type of physics only. Also, when solving 2D models, direct solvers are used as default.
In the mf, mef, and rmm interfaces, there is a domain feature called Gauge Fixing for A-field. The feature is available except when solving for the out-of-plane vector potential only in 2D and 2D axisymmetry. The Coulomb gauge \nabla \cdot \textbf{A} = 0 is then trivially fulfilled as the vector potential is assumed constant in the out-of-plane direction.
The Gauge Fixing for A-field feature introduces a Lagrange multiplier \psi to enforce the Coulomb gauge, resulting in two coupled equations. Let’s use magnetostatics as an example. The first equation (static Ampère’s law) is for \textbf{A} and is expressed as
(1)
where \textbf{J}_e is the externally applied current density.
The second equation is for \psi and expresses the Coulomb gauge
(2)
In Eq. 1, the variable \psi acts similarly to the pressure in the incompressible Navier–Stokes equations, where the pressure enforces the constraint of a divergence-free flow field.
As Eq. 1 shows, the magnitude of \psi does not have particular significance; only its gradient enters the equations (it acts like a potential). The \nabla \psi “current-like” term in Eq. 1 closes the set of equations by providing a mechanism for letting \psi affect \textbf{A}. To ensure a nonsingular model, it is important to constrain the value of \psi in at least one point. By default, the feature constrains the value of \psi on magnetic insulation boundaries to a value that can be set in the interface by entering the divergence condition variable scaling \psi_0 (default value 1 A/m). The figure below shows the \psi field and the magnitude of the electric field \textbf{E} for the power inductor model using different \psi_0 values. As can be seen, the magnitude of \psi does not affect the \textbf{E} field.
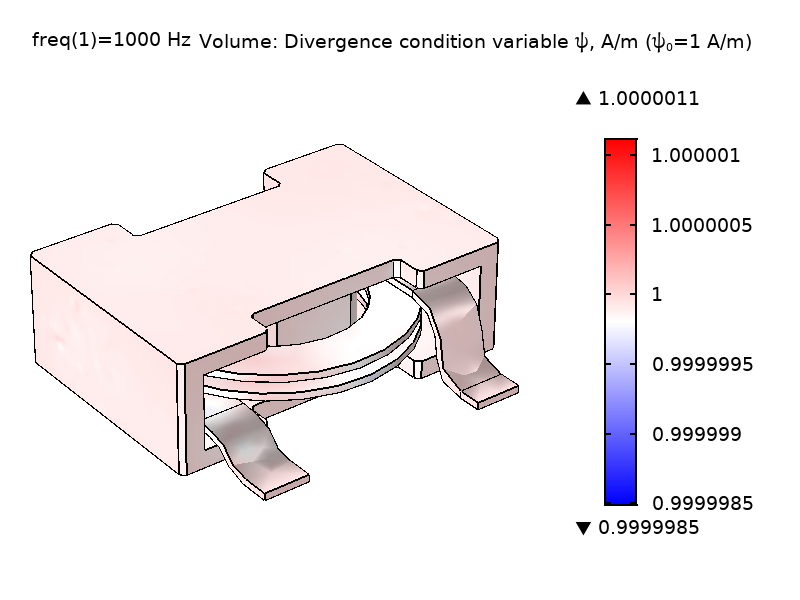
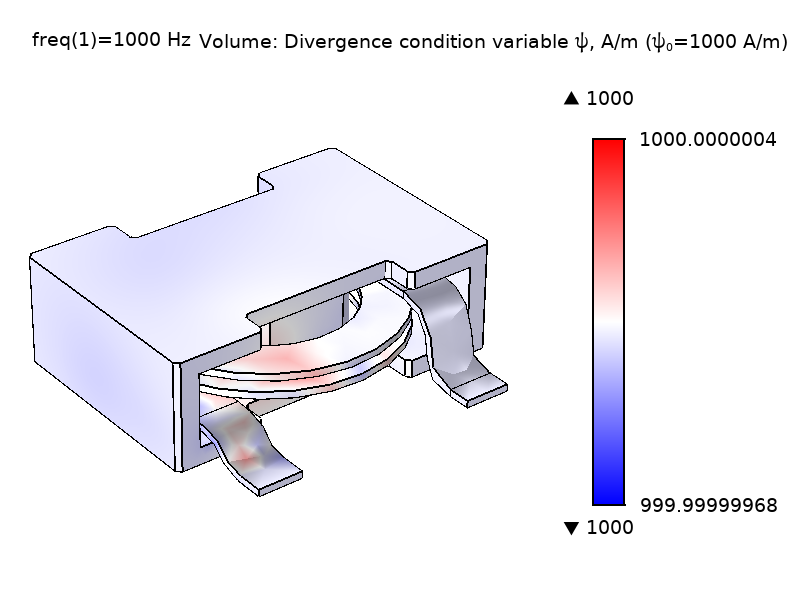
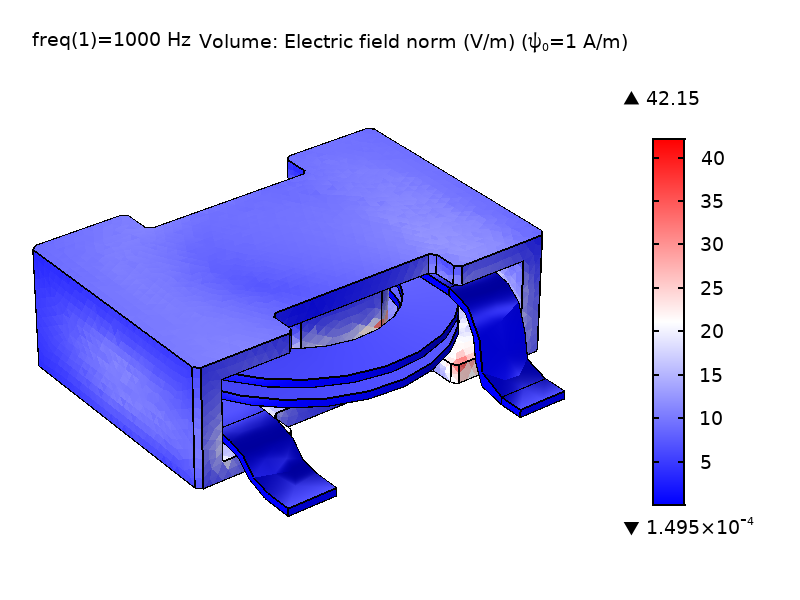
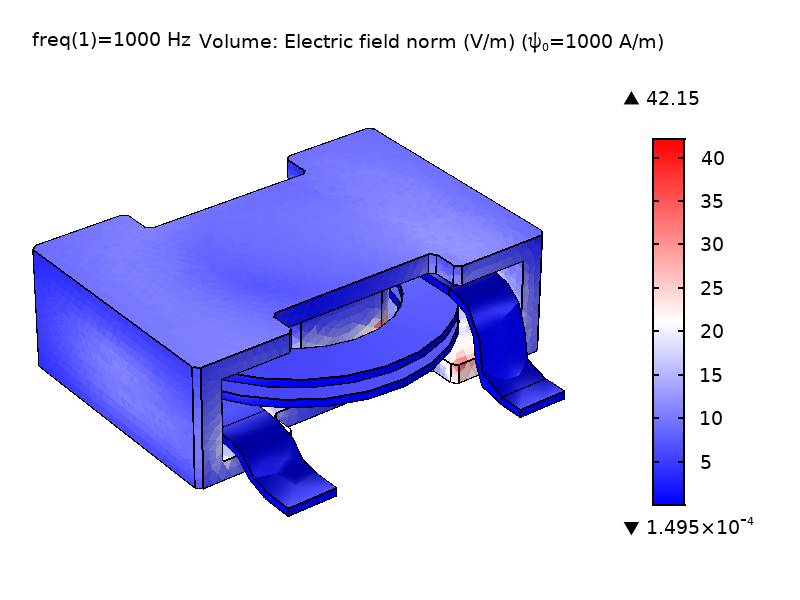
Figure 2: Comparison of the computed \psi field and \textbf{E} field norm in the coil and core domain solved with different \psi scaling; \psi_0 = 1 A/m (left) and \psi_0 = 1000 A/m (right).
It is recommended not to use gauge fixing unless necessary, since it increases the total number of unknowns, requiring more memory and time to solve. Depending on different models, the computation time could increase by 30–60% if gauge fixing is used. It is also worth mentioning that the gauge fixing will result in the system matrix having zeros on the diagonal. The latter is not a problem when using a direct solver, but an iterative solver has to use more expensive methods in the preconditioner (e.g., the Vanka algorithm). Please refer to the COMSOL Reference Manual for details on the solvers. Thanks to the solver defaults normally accounting for the above situations, it is generally not necessary to worry about the change of the structure of the system matrix.
Imposing Current Conservation: Another Role of Gauge Fixing
Current conservation is inherent in Ampère’s law, meaning that the sum of applied source current densities and the induced current density must be solenoidal. This has important consequences when solving Maxwell’s equations. For the static case in the mf interface, the equation to be solved is expressed as
(3)
Taking the divergence of both the left- and right-hand side of Eq. 3 yields
(4)
Notice that the left-hand side of Eq. 4 is zero per definition as \nabla \cdot( \nabla \times \textbf{F}) = 0 for any \textbf{F}. Thus, the right-hand side, the divergence of the external source current density, should also be zero, since otherwise the equation has no solution (at all). This causes the variable \psi introduced in Eq. 1 to effectively serve two purposes. Apart from the obvious purpose of enforcing Eq. 2, it also enforces the condition \nabla \cdot (\textbf{J}_e + \nabla \psi) = 0, which is inherent in Eq. 1. In other words, the added term \nabla \psi in Eq. 1 will eliminate any divergence from the externally applied current density, making the modified right-hand side comply with the required current conservation. For this reason, unexpected solutions can be produced if gauge fixing is used in combination with an externally applied current density that is not divergence free in the analytical sense. Then the gauge fixing will introduce a nonphysical, large compensational current density in the \nabla \psi term and the model will produce unexpected results. This might lead to a misconception and to detect such cases, it is suggested to visualize the \psi field after solving with gauge fixing. The \psi field should only have extremely small variations in the domain where gauge fixing is applied, as shown in the top row of Figure 2. If not, the supplied source current density is most likely not solenoidal as required by Ampère’s law. Here, it is appropriate to add that the default iterative solvers for the stationary solution of the Magnetic Fields (mf) interface perform a similar correction of the supplied source currents so the gauged and ungauged solutions will not be different when it comes to the physical field \textbf{B}.
For the dynamic cases in the mf interface (\sigma, \omega>0), the solution is unique and constraining \nabla \cdot \textbf{A} = 0 is usually not necessary. The mf interface provides an option to switch the gauge fixing from Stationary (\nabla \cdot \textbf{A} = 0) to Study controlled, so let’s elaborate more on what that means. In the time-dependent study, the mf interface solves the equation:
(5)
It considers the induced conduction current density but ignores the induced displacement current density (so-called quasistatic approximation). In this case, instead of constraining \nabla \cdot \textbf{A} = 0, the study-controlled gauge fixing reduces to help imposing current conservation by enforcing \nabla \cdot (\sigma \textbf{A}) = 0, which is consistent with taking the divergence of Eq. 5. Similarly, for the frequency domain study, which includes both types of induced current densities and is a “full Maxwell formulation”, instead of constraining \nabla \cdot \textbf{A} = 0, the study-controlled gauge fixing enforces \nabla \cdot \textbf{J} = 0 for the total current density \textbf{J}. The main benefit of using this kind of divergence constraint is improved numerical stability, especially when approaching the static limit.
Try It Yourself: Experiment with Gauge Fixing
To get a better understanding of gauge fixing, it is helpful to do some experiments by yourself. The table below lists some models in the Application Library that you can solve without and with gauge fixing and then compare the results and computation times. For example, in the E-Core Transformer model, it is solved with gauge fixing with a direct solver and the electrical conductivity is set to zero. You can also solve it with the same direct solver without gauge fixing by setting \sigma=1 S/m in all domains and also in the stabilization electrical conductivity for coil domains. You will notice that the model can be solved within about half of the computation time when gauge fixing is used.
| Physics Interface | Study Type | Model in Application Gallery |
|---|---|---|
| mf | Stationary | Helmholtz Coil |
| Time-Dependent | E-core Transformer | |
| Frequency Domain | Eddy Currents | |
| mef | Frequency Domain | Power Inductor |
| rmm | Time Dependent | Permanent Magnet Motor |
Summary
In this blog post, we started by emphasizing that gauge fixing is not necessary in electromagnetics simulations with the AC/DC Module unless you need to use a direct solver. Then we showed how gauge fixing is implemented and used in three related physics interfaces, followed by discussing benefits and drawbacks of gauge fixing. At the end, we provided a list of interesting models that you might want to experiment with.




Comments (8)
Julian Anaya
October 27, 2020Perhaps I am mistaken but I just noticed that equation 5 seems to be wrong… it seems that there is an extra J term there (sigma * A’ is already the ohms law so it equals J right? ). Also form the equation in the module which reads curl(H)=J it follows that curl(curl(A))=J=sigma * A’ , which corresponds to equation 5 with J=0.
Kind regards
Lipeng Liu
October 27, 2020 COMSOL EmployeeHi Julian,
The J term in equation (5), having the same meaning as that in other equations, is the externally applied current density. It is not the total current density. The meaning of J might be different in a different context.
Regards,
Lipeng
Julian Anaya
October 28, 2020Dear Lipeng, thanks for clarifying this but I find quite confusing the nomenclature then. In the MF interface, J is defined as J=sigmaE+Je; i.e J=-sigma * A’+Je. Then equation 5 is curl(curl(A))=-sigma * A’+Je=> sigma * A’+curl(curl(A))=Je. Please note that in the article it is impossible to distinguish when J refers to the total current density or just to the external part as in this case (for instance in divJ=0, that J is the total J, not the Je).
Kind regards,
Julian
Lipeng Liu
October 28, 2020 COMSOL EmployeeHi Julian,
Thanks for pointing out this. In this article, the J in equations (1),(3),(4) and (5) should be changed to Je. I will make modifications accordingly here as well as in the interface to avoid confusing.
Regards,
Lipeng
Julian Anaya
October 28, 2020You are welcome Lipeng 🙂
Jens Krause
December 4, 2024Hi Lipeng,
thanks for this explanation, really helpful. What about the case when there is a Lorentz-term in 3-D? E.g. in an eddy current brake I want to use this method to reduce the problem to a stationary solution. Do I have to use gauge fixing.
Regards
Jens
Lipeng Liu
December 4, 2024 COMSOL EmployeeHi Jens,
In this case and in line with the blog post, gauge fixing is optional. Please check out this library model: https://www.comsol.com/model/magnetic-brake-2014
Regards,
Lipeng
Jens Krause
December 10, 2024Hi Lepeng,
thanks for the hint. If I look at the library example I see that the iterative solver is used. If I want to (or have to) use a direct solver I need to switch gauge fixing on in this example.
Regards
Jens