
When designing and modeling devices such as chemical reactors, one of the quantities used to characterize the system is the residence time. This calculation is separate from the computation of the flow field, and can be done using the Particle Tracing Module. Let’s learn more…
Computing Residence Time and Other Factors
Let’s suppose that we are modeling a small flow cell, similar to a biosensor. We start with a fluid dynamics analysis, computing the flow of water around a set of obstructions. In this case, we can reduce the problem to a two-dimensional computational model, as shown in the image below.

Image of water flow around obstructions in a reactor.
Once the flow field is computed, we also want to plot and compute the following:
- Residence time distribution function
- Cumulative distribution function
- Mean residence time
- Variance
To solve for these quantities, it is most convenient to use a Lagrangian formulation to trace a computational particle as it moves with the fluid, rather than using the Eulerian formulation used to solve for the flow field. For this reason, as well as the built-in features available for conveniently evaluating particle tracing results, we will address this using the capabilities of the Particle Tracing Module.
Using the Particle Tracing Functionality in the COMSOL® Software
The use of the Particle Tracing Module to trace streamlines of the flow field, and to integrate along these streamlines, is covered in this Learning Center article on integrating along streamlines and extracting particle statistics. Along with those methods, there are additional techniques to bookkeep the particles in the flow, as described in a previous blog post, “Different Ways to Count Particles in COMSOL Multiphysics®“.
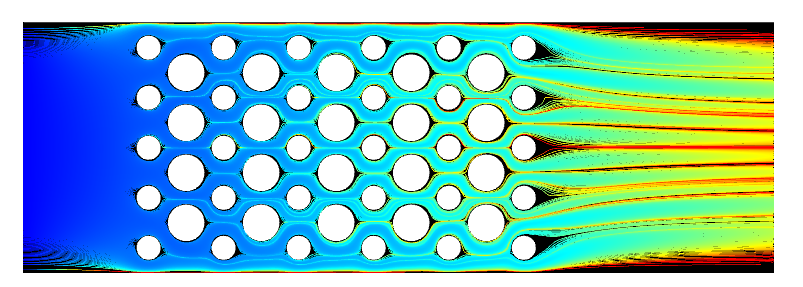
Streamlines of the flow, colored by the time it takes a particle traced along the flow to reach that point.
The results shown above visualize the time of a computational particle being traced along the streamlines. The residence time distribution and the cumulative distribution at the outlet are shown in the plots below. It’s additionally possible to extract scalar values such as the mean residence time and variance, as described in the Learning Center article mentioned above.
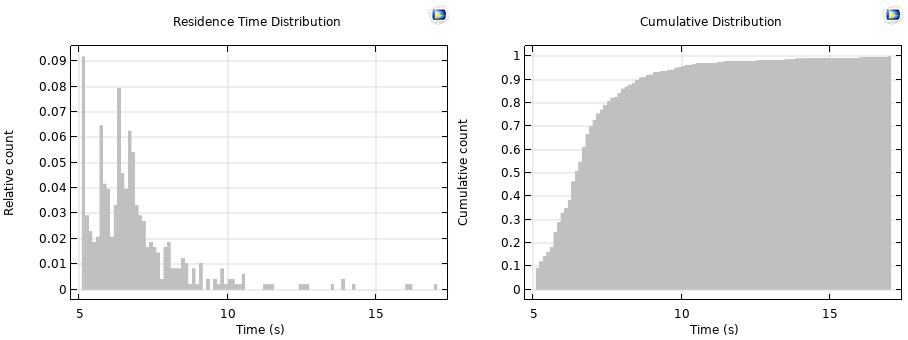
Plots of residence time distribution (left) and cumulative distribution (right).
Closing Remarks
Here we have only traced the streamlines of the flow field, but the functionality of the Particle Tracing Module has wide-ranging applications for augmenting the analysis of flow fields. It is particularly useful, as its name implies, when we want to consider actual particles in the flow, in which case we can also include the effects of:
- Particle inertia
- A distribution of particle sizes
- Changing of size/mass during transit
- Arbitrary additional governing ODEs solved with the moving particle
- Forces on the particles
- Drag
- Turbulent dispersion
- Lift
- Gravity
- Centrifugal
- Electric
- Dielectrophoretic
- Magnetic
- Magnetophoretic
- Brownian (molecular diffusion)
- Thermophoretic
- Acoustophoretic
- Particle–particle interaction
- Coupled fluid-particle interactions
For an overview of the other formulations that are available, see this previous blog post on particle tracing in fluids.
Next Step
Learn more about the specialized features and functionality in the Particle Tracing Module by clicking the button below.







Comments (7)
Alan Collier
June 9, 2021The traditional method for measuring a residence time distribution is to inject a tracer pulse at t=0 and measure the outlet concentration as a function of time. It would be interesting to see a comparison of these methods in this case.
On a related question – is there a convenient way to do a time integral on an outlet stream, for example to generate the cumulative residence time distribution from the outlet concentration and flow velocity in this case?
Walter Frei
June 9, 2021 COMSOL EmployeeHello Alan,
Yes, that is an alternative approach, but one big drawback to that will be that the solution time will be dependent upon Peclet number. (High Peclet number will lead to longer solution time.) The particle tracing approach will be faster, and also makes data extraction & statistics simpler.
Wallace Huang
July 15, 2021Dear Mr. Walter,
Thanks for your excellent guidance. I have always learned a lot from your blogs.
About particle tracing module, have you ever experienced problems like ” Some particles have been removed from the simulation because maximal number of wall interactions within one time step has been reached.”
When a bounce condition is chosen in the simulation, the particles disappear after it makes contact with the wall.
Could you kindly share your advice on how to solve this kind of problem? Thank you!
ARVIND BAIRWA
October 1, 2021Hello Walter Frei,
I am calculating the drag coefficient of an array of cylinders (120 cylinders).
I am using this expression,
sum( -reacf(u)*2, x, 1,120)/(spf.rho*U_mean^2*d)
which says drag force summation from 1 to 120 cylinder having ‘U_mean’ velocity and ‘d’ diameter. However, it does not seem to work. Could you please suggest a correction in this expression?
Thank you
Walter Frei
October 1, 2021 COMSOL EmployeeHello Arvind,
See: https://www.comsol.com/blogs/how-do-i-compute-lift-and-drag/
Jorge Belgodere
March 31, 2022I am having trouble linking the residence time to the particles. They seem to not accumulate time as the travel down my fluidic channel. Would it be possible to release your COMSOL file in a format viewable by version 5.3?
Walter Frei
March 31, 2022 COMSOL EmployeeHello Jorge,
We do encourage you to upgrade to the most recent version, version 6.0, there are a number of significant enhancements: https://www.comsol.com/release/6.0