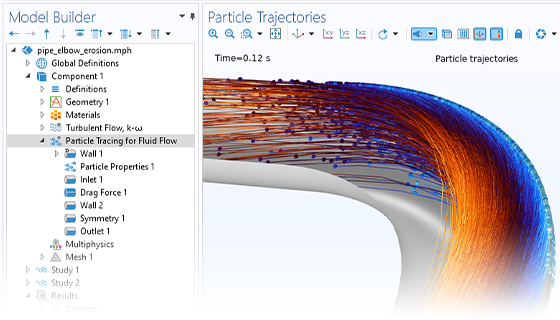
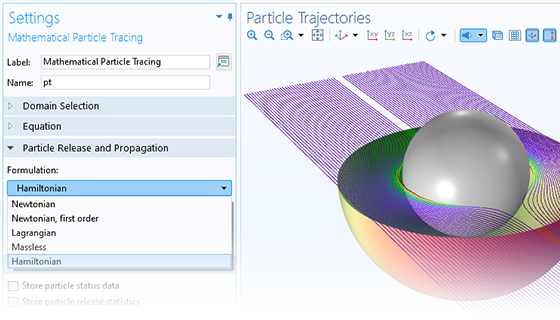
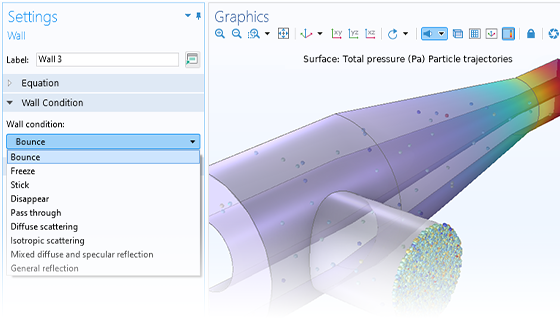
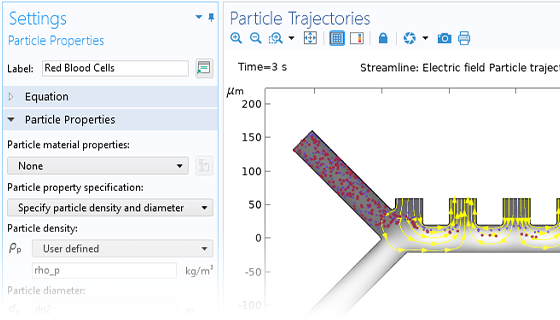
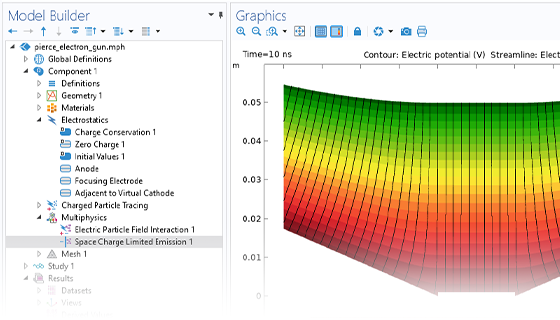
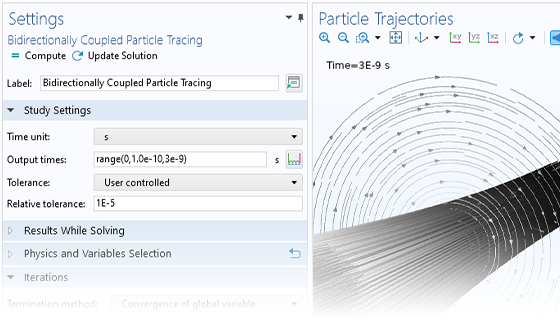
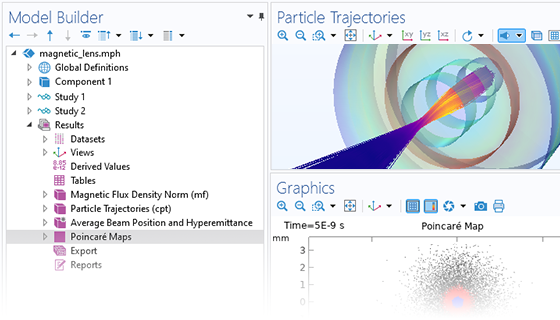
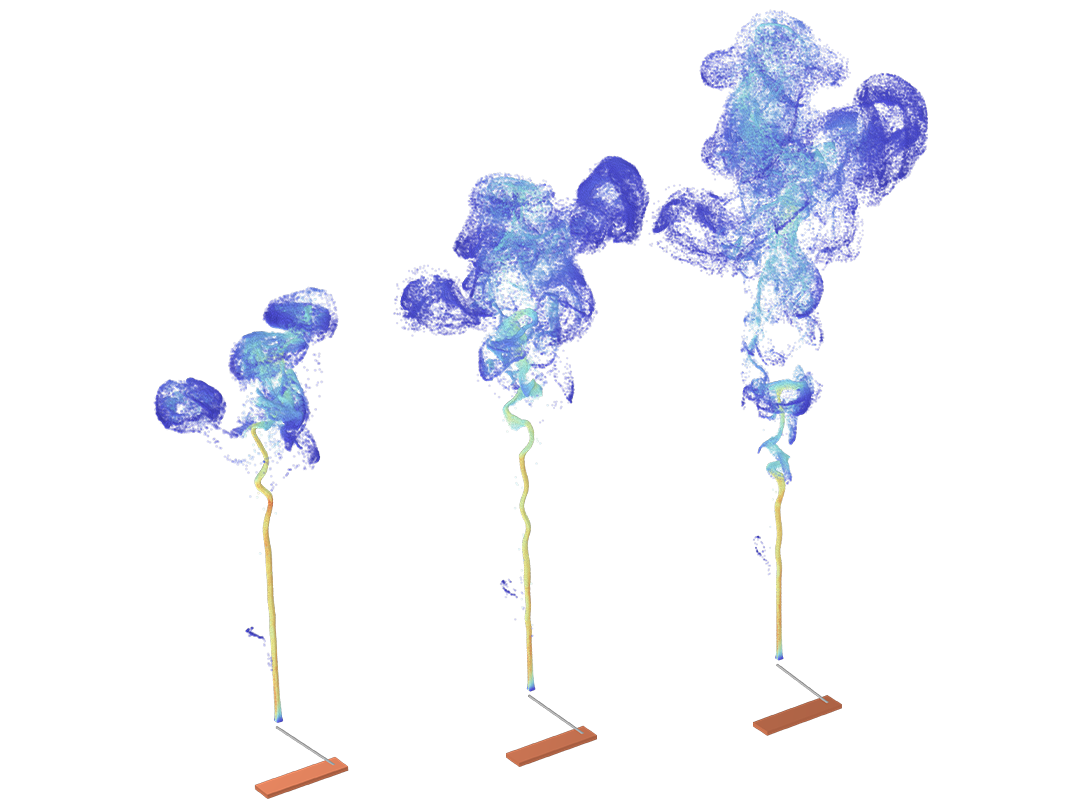Charged Particle Tracing
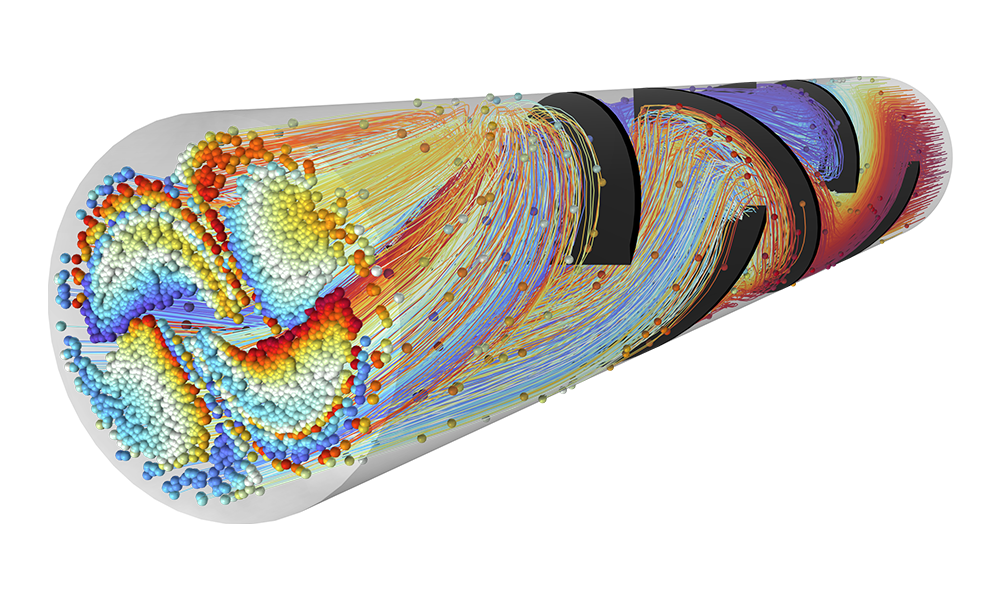
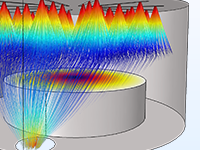
Accurately predicting the motion of ions or electrons in applied fields is essential to the design of spectrometers, electron guns, and particle accelerators. The applied fields might be user defined or taken from a previous analysis. Such fields can be stationary, time dependent, or solved for in the frequency domain. You can apply any number of different fields, allowing you to superpose stationary and time-harmonic fields in the same simulation.
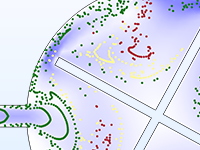
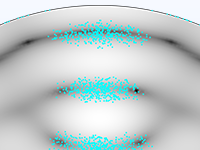
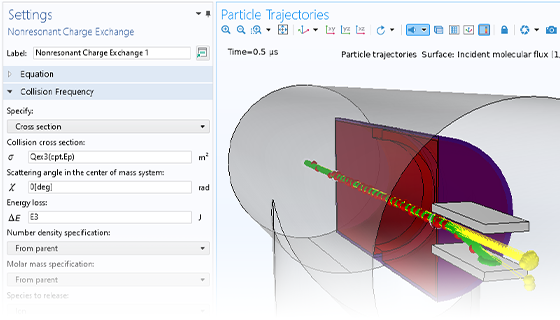
Particle motion seldom takes place in a perfect vacuum. You can turn any particle tracing model into a Monte Carlo collision model, giving the particles some chance to collide with molecules in the surrounding gas. This might cause particles to change direction or even undergo reactions such as ionization and charge exchange.
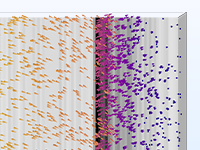
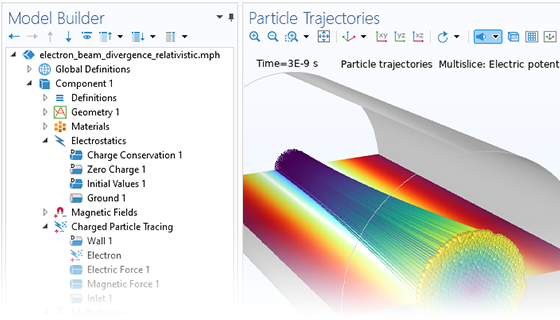
The simplest charged particle tracing models involve unidirectional (one-way) coupling, where the fields are solved and then used to define forces on the particles. If the charged particles are in a beam of sufficiently high current, it might then be necessary to consider the bidirectional (two-way) coupling, where the particles can perturb the field. Built-in analysis types are available to conveniently set up bidirectionally coupled models.