
Lightweight and portable washing machines are great to use in situations where you do not have access to traditional washing machines. Yet problems may occur when a varied distribution of clothing causes walking instability in these machines. We tested for walking instability during the spin cycle of a portable washing machine and used an active balancing method in an attempt to remove this instability.
A Lightweight Machine
Not everyone has access to a laundry room or the ability (or time!) to go to a laundromat. You may not want to spend your change on coin-operated machines or leave the warmth of your apartment to go to a laundromat. Portable washing machines are a solution to these problems. They do have their own setbacks, though. The lightness of these machines coupled with an unbalanced distribution of clothes causes them to become unstable.
When the laundry is in a spin cycle, it generates a centrifugal force — causing the machine to destabilize. This problem could be solved by making the washing machine heavier, but since this machine is meant to be portable, this isn’t an ideal option. To learn more, we turn to simulation.
Simulating a Portable Washing Machine Model
For this problem, we chose to model a simplified horizontal-axis front-load washing machine (the horizontal model has more severe instability than the vertical version). We used this model to figure out how walking instability affects the washing machine during a spin cycle. In order to try to remove the instability, our model makes use of an active balancing method.
Model Assumptions
In order to simplify our model, we made a few assumptions.
Assumptions about the drum and washer:
- Both are rigid.
- The rotation around the axis of the drum is the sole relative motion between the drum and the washer.
- The laundry spins at the same speed as the drum. We assume this because the RPM of the drum is high enough to produce substantial centrifugal forces.
Assumptions about the machine’s interaction with the surrounding environment:
- The washing machine cannot tip over. It remains connected to the ground throughout the simulation.
- The Coulomb friction model, with a constant friction coefficient, is used to simulate friction between the washer and the ground.
Designing the Model Geometry
When setting up the model, we have to pay attention to where everything is placed. The balancing mass should be placed on both sides, the front as well as the back side, of the drum however for the ease of modeling, we place the balancing mass only on the front side of the drum making sure that its center of mass moved to the center of mass of the drum. When calculating mass, we need to remember that the mass of the drum adds to the clothing mass.
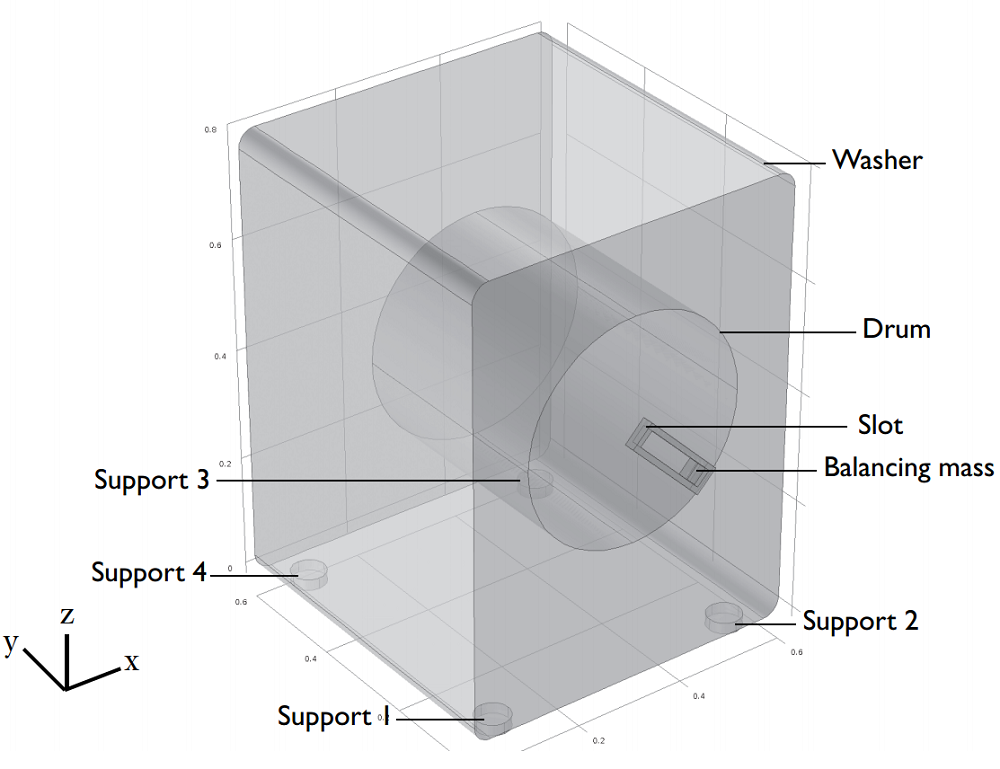
The drum is connected to the washer and the slot through hinge joints and a prismatic joint connects the slot and balancing mass. Both the joints, hinge joint connecting the drum to the slot and the prismatic joint, are necessary for active balancing, as we will learn more about in the next section. (Please note that in our model the prismatic joint is always locked since it isn’t used, while the drum/slot joint is only locked when there is no balancing in the system.)
Planar joints function as the washer’s four supports and connect the washer to the ground at four separate points. We’re able to analyze the joint forces independently on all joints because the joints have elasticity.
Slip Margin and Active Balancing
The instability of our washing machine model could result in multiple kinds of slip. For our needs, though, we are focusing on rotational slip and instability, since it happens at a lower critical speed than translational slip.
We measure our model’s stability by using the slip margin. Slip margin is the difference between the maximum possible friction force and the actual friction force. In the case of our example, it decides the critical operational speed needed to avoid walking instability. Walking instability will happen when the slip margin reaches zero. Our machine slips when three or more of our supports have a zero slip margin.
In order to make our machine more stable, first we have to eliminate what is making our washing machine unstable. In this case, the culprit is the net unbalanced centrifugal force acting on the rotating clothing. To combat this, we can apply an equal and opposite force. This is where active balancing comes into play.
To balance the forces within our machine, we adjust the angular and radial positions of the balancing mass. An angular correction serves to fix the direction of the centrifugal force and can be achieved by rotating the slot-balancing mass in relation to the drum. A radial position fixes the magnitude of the centrifugal force through the translation of balancing mass in the slot. In our simulation only angular correction is required because the radial position of the balancing mass is already set based on the weight of the laundry.
Our model makes it easy to use active balancing. Since we know the angular drum speed and acceleration rate of our model, we can activate our balancing system at a specific time instead of waiting for the slip margin to get close to zero.
The Results
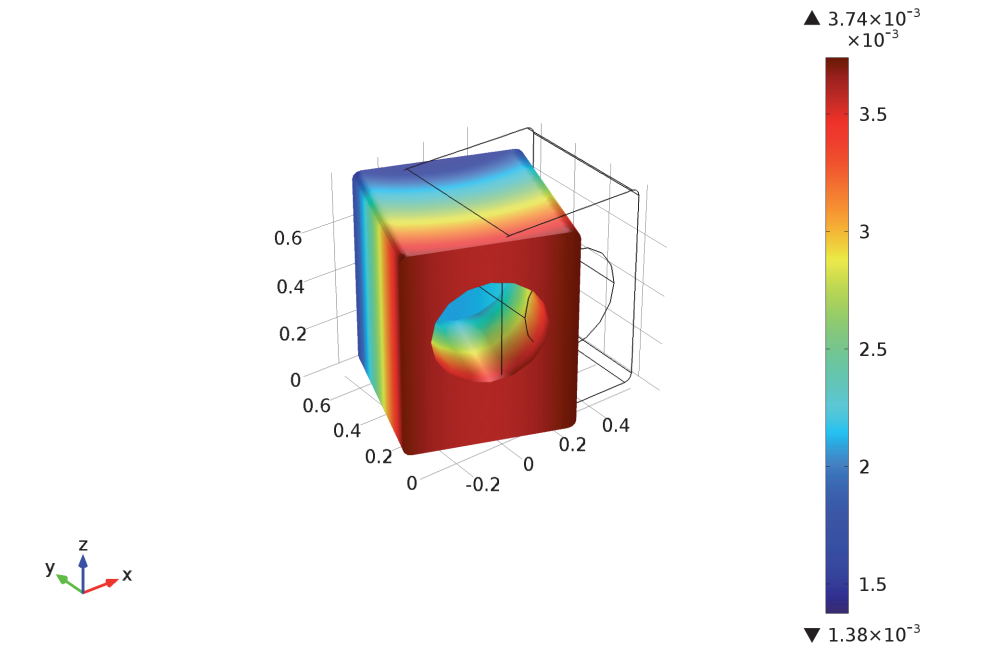
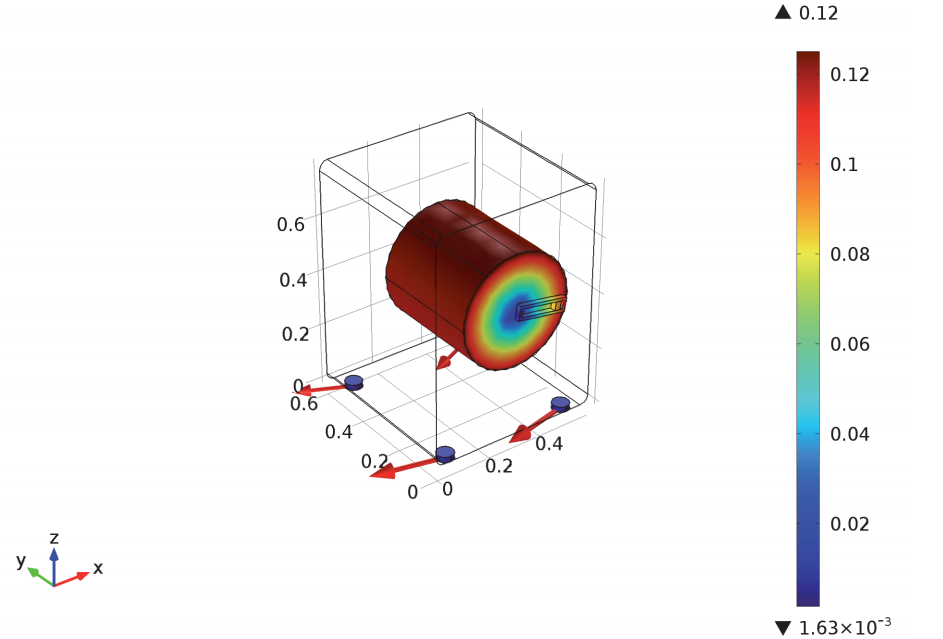
After taking all the previously mentioned factors into account, we ran our simulations. At first we looked at our washing machine without the aid of active balancing:
Left: The washer rotation (magnified by a factor of 100). Right: The drum rotation and friction force at the washer supports.
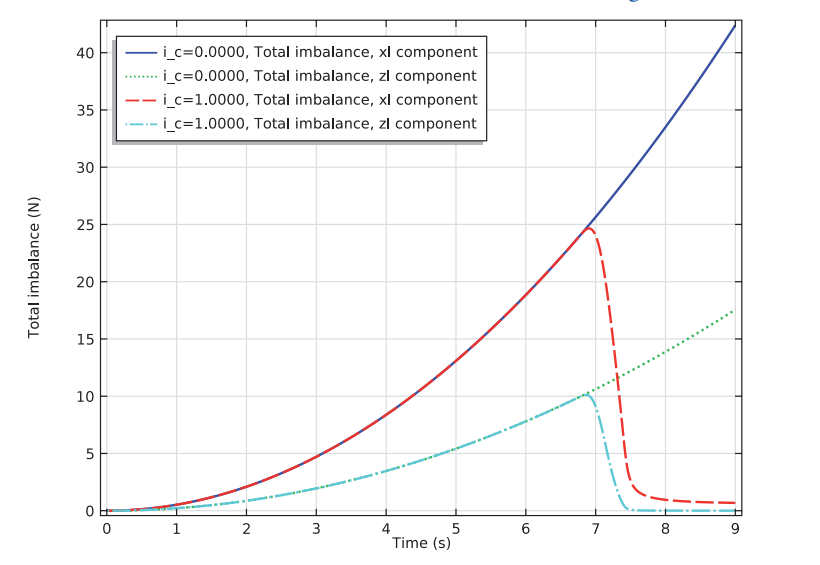
Next, we saw what happens when we add active balancing to our simulation by viewing the total imbalance of our washing machine in two ways.
Our first plot shows the imbalance in the rotating frame and displays a clear correlation between active balancing and reduced imbalance. A similar effect is viewed in the fixed frame plot.
Left: Total imbalance in the rotating frame. Right: Total imbalance in the fixed frame.
Another area we looked into was the slip margins of our model. First, we analyzed the differences in the individual supports without active balancing. We compared the slip margin of a support in the front of the washing machine (support 1) and a support in the back (support 3). The plot to the left below reveals that the a washer with front support has a lower slip margin and is therefore more prone to slipping than a washer with back support.
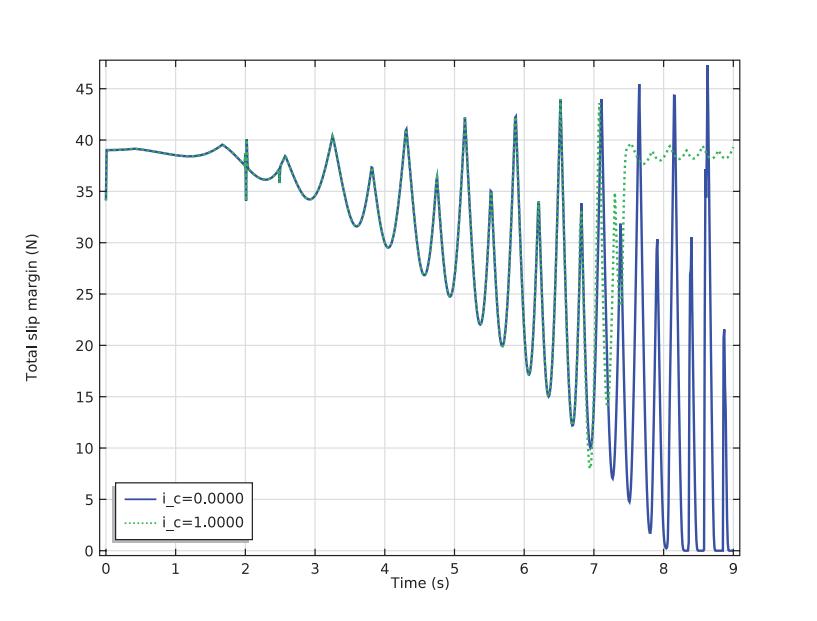
Widening the parameters to look at the total slip margin of our model, we saw that the total slip margin does become zero for short periods. This means that the washing machine will experience walking instability during these moments. The right-side plot shows that active balancing increases the total slip margin upon activation.
Left: The slip margins of supports 1 and 3 in the absence of active balancing. Right: The washing machine’s total slip margin with and without balancing.
Active balancing is further shown as helpful when looking at the movement of the washer around a vertical axis. Rotational instability is eliminated with the balancing mechanism.
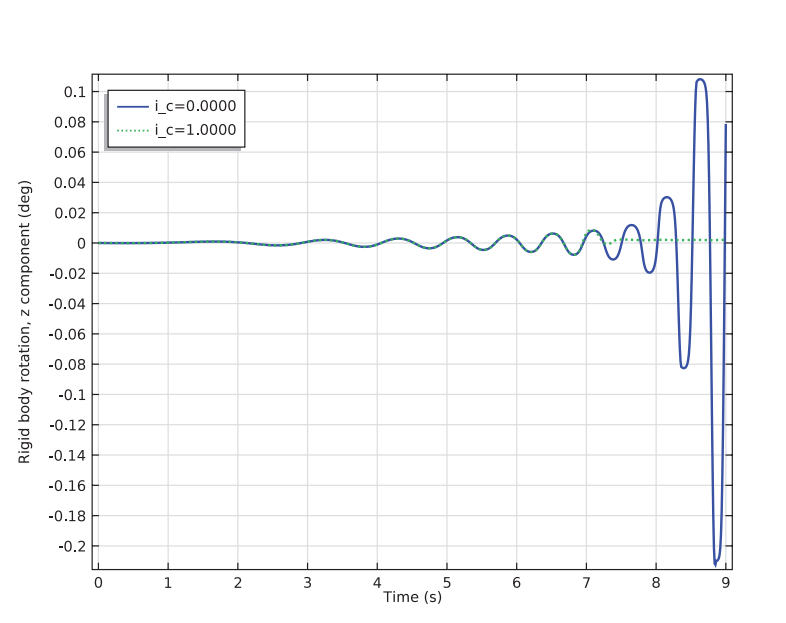
The Z-axis rotation of washer with and without balancing.
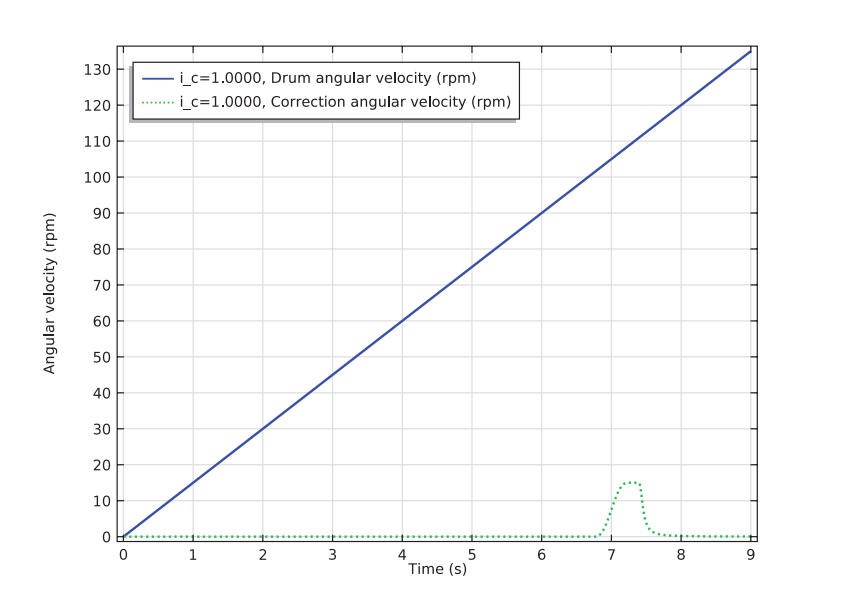
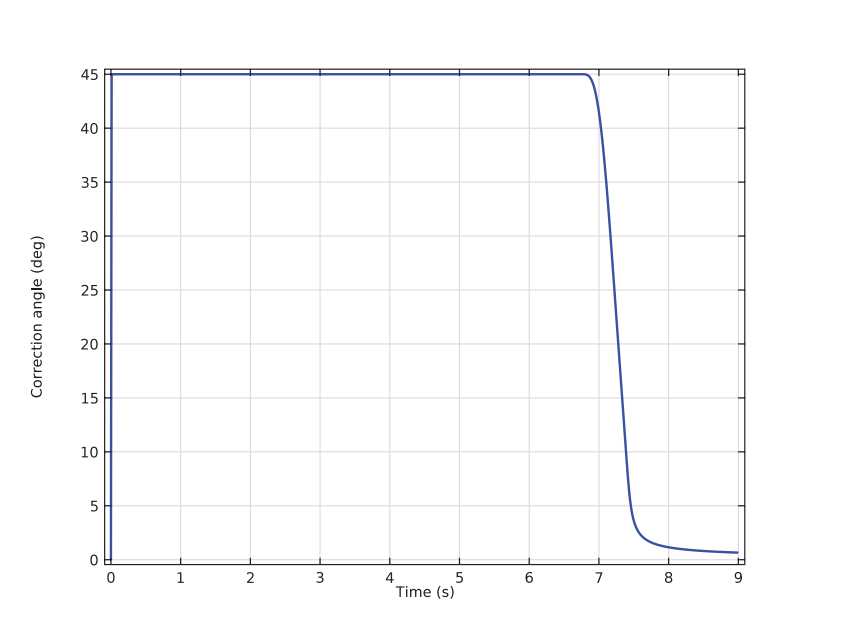
We modeled other aspects of our portable washing machine as well. When looking into the revolutions per minute (RPM) of the drum and correction motor, we found that the correction motor works efficiently by starting when needed and stopping when the system is stabilized. We also calculated the appropriate correction angle for stabilizing the system.
Left: RPM of the correction motor and the drum. Right: The necessary correction angle in an active balancing system.
Creating an active balancing system helped our model avoid the effects of walking instability and rotational slip during its spin cycle. Now it’s your turn to try it out yourself — download the model via the link below to get started.
Further Reading
- Model download: Walking Instability in a Washing Machine
- Related blog post: Simulating Vibration and Noise in a Washing Machine






Comments (0)