One of the most common uses of the AC/DC Module is for modeling electromagnetic coils and the interactions with their surroundings. Today, we will look into one of the key concepts to keep in mind when modeling coils: closing the current loop. If your work involves modeling coils, you will need a complete understanding of this topic.
How to Model a Basic Coil in COMSOL Multiphysics
Let’s start with a simple example of a conductive wire that is bent into a loop and connected to a constant voltage source, a battery (shown below). Due to the voltage difference, a current will flow through the wire. The magnitude and direction of this current throughout the conductor can be computed from Ohm’s law and the Charge conservation equation, along with a set of boundary conditions.

A very simple electromagnetic coil connected to a DC voltage source.
For this single wire, we can consider a grounded boundary condition at one end, meaning an electric potential of zero, and a higher electric potential on the other end. Current cannot flow in or out of the wire anywhere else, so the electric insulation condition is applicable on the remaining boundaries. This problem can be solved using the finite element method as implemented in the AC/DC Module in COMSOL Multiphysics.
As a consequence of the computed current flow, a magnetic field arises and surrounds the wire. This is a vector field, having both a magnitude and direction, and can be computed from Ampère’s law. We are interested in learning how to model this magnetic field and how it interacts with other objects.
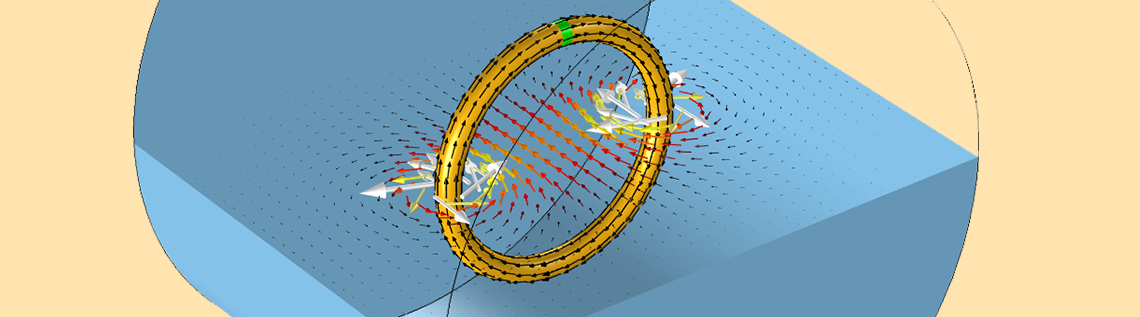
For the purpose of learning coil modeling, we won’t concern ourselves with exactly what is happening within the source itself. Instead, we will just assume that a device exists that provides a constant voltage, or a constant current. We also won’t concern ourselves with the wires between the coil and the source, but assume that they are electrically insignificant. Based upon these two assumptions, we will say that a reasonable computational model of a coil might look like the image below, which shows a single wire with a single turn as well as the surrounding magnetic field due to the current flow.

A computational model of a coil with one turn. The current flow (black arrows) in the wire results in a magnetic field (colored arrows) in the surrounding air region.
There are actually a couple of other assumptions that have gone into solving the above model. First, we can see that there is a cylinder around the coil representing the air domain. This is the computational domain within which we are solving for the magnetic field. This is a finite-sized domain, yet the magnetic field will actually extend infinitely far away from the coil. The field intensity will drop off with the inverse of distance to a straight wire, so the field magnitude will be quite small far away from the coil. Although it will never be precisely zero, we can reasonably truncate our modeling domain to a finite-sized space.
By choosing a finite modeling region around the coil, we are assuming that we are only interested in the fields in this region. This choice of finite-sized region introduces another assumption at the boundaries. We need to consider some boundary conditions along the boundaries of the cylinder or whatever surrounding domain shape we choose. We will discuss the various possible boundary conditions, their physical interpretations, and why to use each one at length in a later blog post, but for this particular case, we will consider a boundary condition that represents a perfect electrical conductor.
For the physical interpretation of this, we assume that our coil sits inside of a cylindrical metal container. As a consequence of the boundary condition, the current, which is flowing along the wire from one end to the other, will flow back along the surface of the modeling domain as shown in the image below.
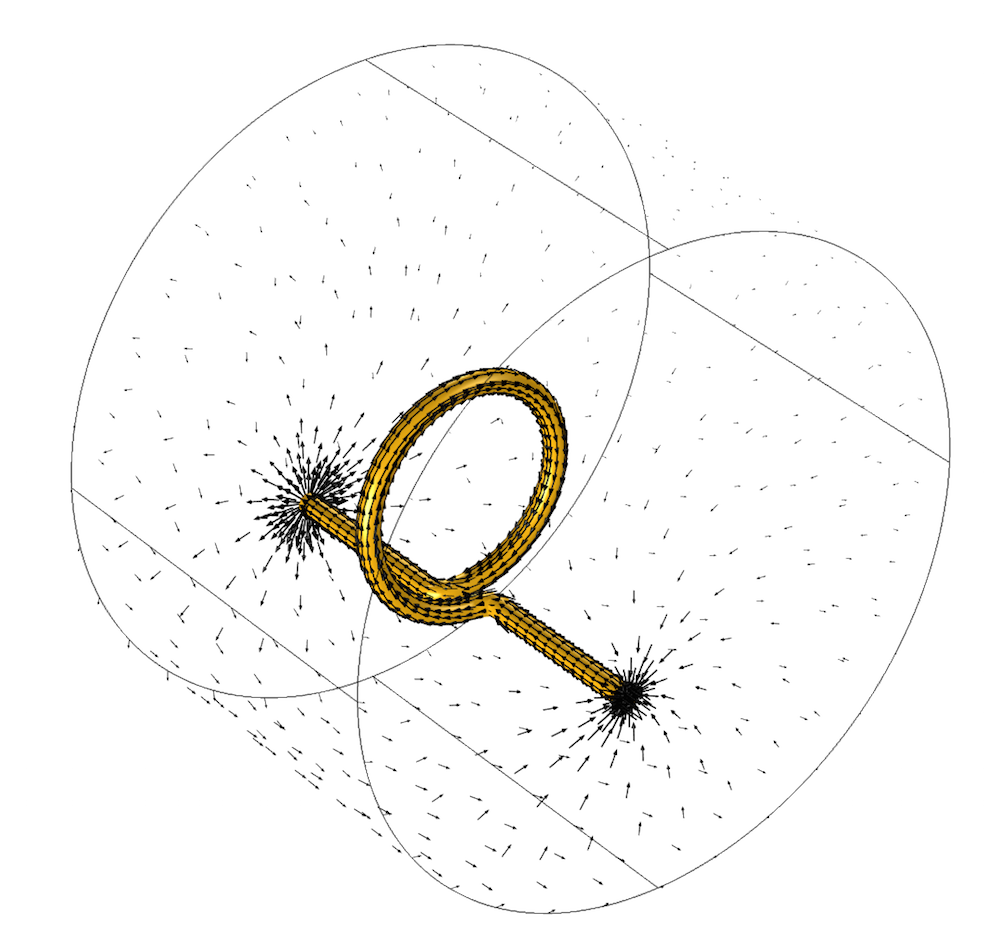
The arrows show the current flowing through the wire and back along the surfaces truncating the modeling domain.
This brings us to one of the most basic points in coil modeling: the concept of a closed current path.
An Important Modeling Condition: Closed Current Paths
Whenever you are modeling a coil, or any magnetic field excited by a current flow, you must have a closed path (loop) of current. Your models must satisfy this condition to be valid. If you would try to impose a current flowing through an open circuit coil, that would be equivalent to implying that the current (electrons) instantaneously moves from one end of the open coil to the other, and this would violate Maxwell’s equations. The image below illustrates one such invalid coil model. Since the coil wire does not extend to the boundary, there is no continuous path along which the current can flow.

An invalid coil model. The current-carrying wires do not reach the boundary, so there is no way for the current to loop back and no current can flow.
Closing the Current Path Within the Model
We can take an alternative approach to our coil model by revisiting some of our assumptions. One of the assumptions that we made in the above example is that the source is outside of our modeling domain. We can, however, alter our model in a way that the source is within our modeling space.
In the image below, one such representative model is illustrated. A closed coil is shown with a small region representing the source that feeds the coil. This source (shown in green in the image below) is entirely within the modeling domain and closes the current path. It is also assumed that the wires feeding the coil are unimportant for our modeling needs and it is assumed that a closed torus is a reasonable approximation of the coil.
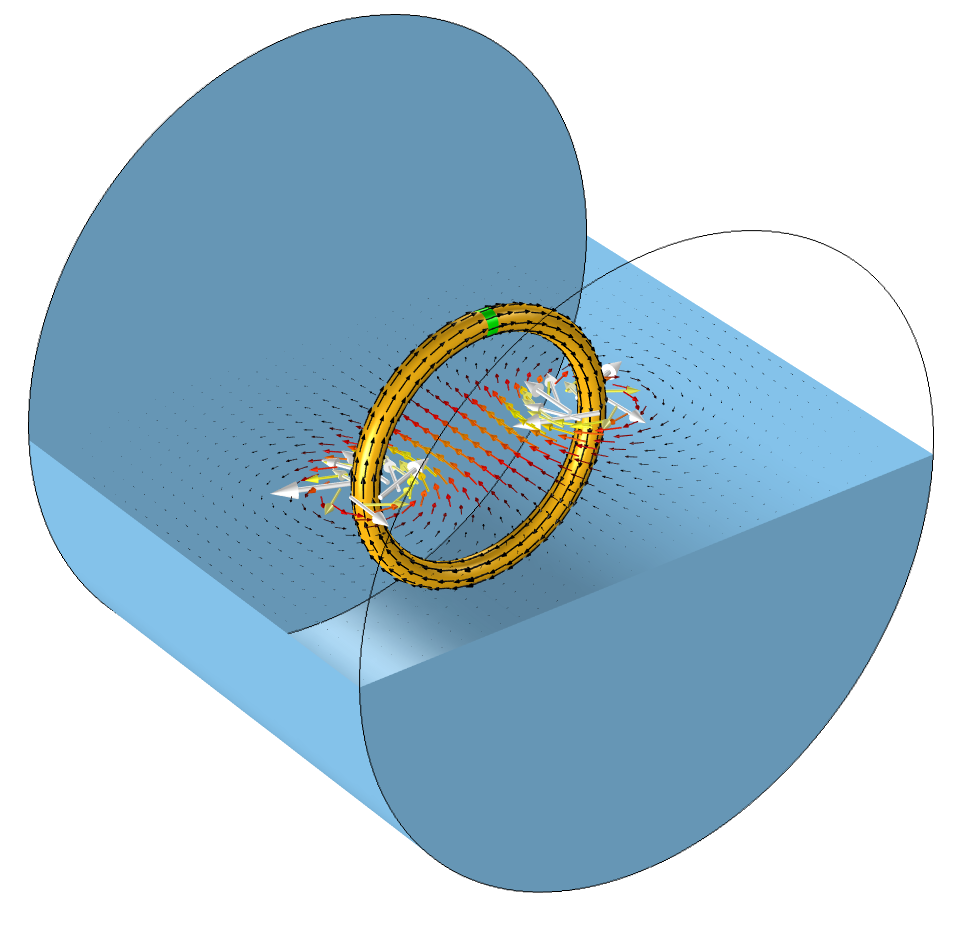
A coil model with the source inside of the modeling domain. The source is the small green section. The coil has a current return path entirely within the modeling domain. The current flow (black arrows) in the wire results in a magnetic field (colored arrows) in the surrounding air region.
An interesting consequence of this approach is that the boundaries of the modeling domain no longer need to provide a current return path. This opens up the possibility for alternative boundary conditions on the exterior of the modeling domain, which can be used to model an insulative surrounding or to approximate an infinite space rather than an enclosing conductive container. We will address the various appropriate ways to truncate a modeling domain in depth at a later point.
Closing the Current Path in Two-Dimensional and Axisymmetric Models
For 2D and axisymmetric models, we also need to concern ourselves with the current return path, so let’s take a quick look at the valid configurations for these cases. An axisymmetric model is appropriate to use when the situation that you want to address is invariant, or nearly so, around an axis of rotation. The image below shows one such 3D geometry, and the associated axisymmetric 2D model. All fields are assumed to be invariant around the axis of symmetry, so the formulation itself takes care of closing the current path, thus we only need to model a 2D domain in the positive rz-plane.
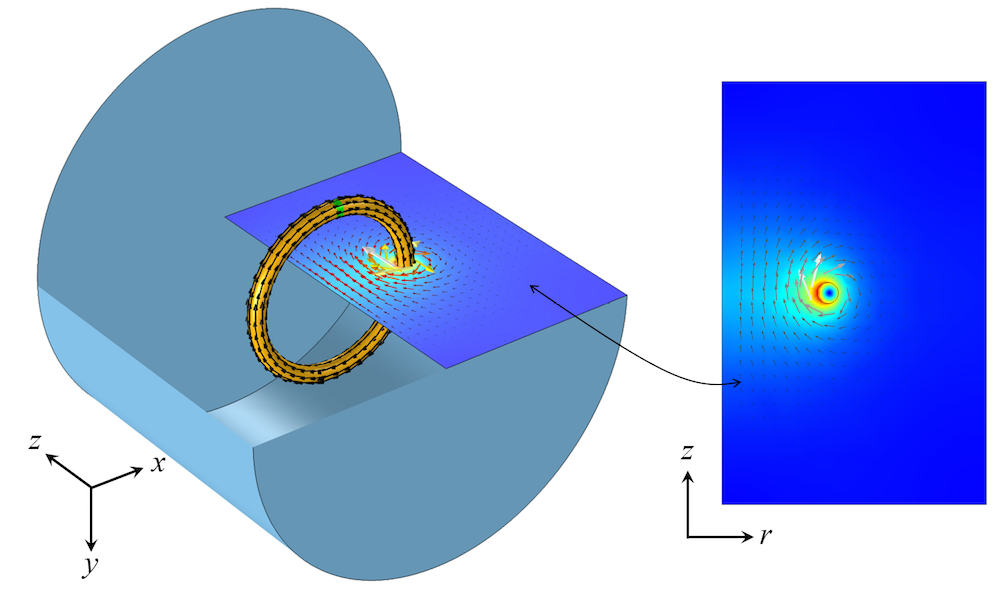
A 3D rotationally invariant coil can be modeled in the axisymmetric 2D plane.
If the coil is very elongated, with negligible end effects such as those seen in motors, then it is also possible to reduce the model down to a simplified 2D model with two different choices for closing the current path. It is possible to model either a cross section of the entire coil, the wires carrying current in opposite directions, or only one half of the coil with a symmetry condition at the centerline.

An elongated 3D coil model. If the end effects are neglected, this can be modeled in a 2D plane.
When both turns of the coil are modeled, one turn carries current perpendicularly into the 2D modeling plane, and the other turn carries the current perpendicularly out of the 2D modeling plane. When only one turn is modeled, a symmetry condition must be used at the centerline that permits current to flow back in the opposite direction. The boundary of the 2D modeling plane closes the current path. These two cases are illustrated below.
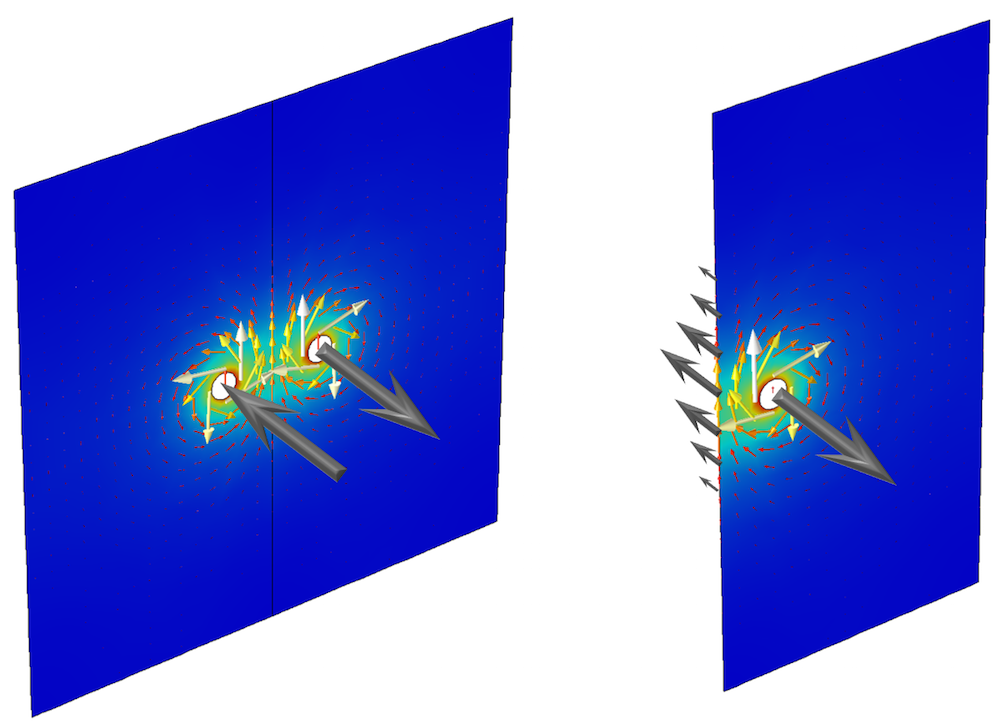
Two different approaches to modeling an elongated coil in the 2D plane. The current flowing in the positive and negative out-of-plane directions (gray arrows) flows along either the coil or the symmetry boundary condition.
Concluding Thoughts on Using the AC/DC Module for Coil Modeling
We have started to look at coil modeling here by introducing the concept of the current loop. If you are modeling a coil, or indeed doing almost any modeling work with currents and the resultant magnetic fields, you will always need to keep this concept in mind. The next topic that we will look at is the question of the appropriate boundary conditions for our computational model, so stay tuned. In the meantime, have a look at these resources:
- Read more about how you can use the AC/DC Module on the COMSOL Blog
- Learn about modeling computational electromagnetics with the AC/DC Module in under three minutes. Watch the video
- If you want to use COMSOL Multiphysics and the AC/DC Module for your coil modeling, please contact us



Comments (19)
Francisco Vallejos
July 1, 2016The instructions PDF for this model are available for download?
yp zhao
July 7, 2016For “Closing the Current Path Within the Model”, if I do not want to use 2-D equivalent model, how to set appropriate boundary condition or excitation to make the current flowing in the 3-D coil with a small gap?
Thanks!
yp zhao
July 7, 2016For the coil, if it is stranded and no eddy-current is allowed there, we can apply a source current density there. But if the coil is solid where eddy-current can appear, then it is not clear how to treat the small gap region. It is helpful to explain more about this point.
Thanks!
Michael Burns
January 6, 2017Not a very useful article.
Bin Sun
March 11, 2017give me a good understanding about coil. Thanks
Bin Sun
March 11, 2017Could you please write more blogs about cable and electromagnetic field? Super interesting and useful. Thanks
AntoineV
January 22, 2018Not useful at all.
No boundary condition is discussed; not a word about the other features : coil geometry analysis, etc…
Sergey Kuznetsov
November 20, 2018I was wondering if there is an example model where it is shown how to use coil geometry analysis?
Sergey Kuznetsov
November 20, 2018How do I use results form coil geometry analysis step in the next step?
Walter Frei
November 21, 2018 COMSOL EmployeeHello Sergey,
An example model which uses the coil geometry analysis is:
https://www.comsol.com/model/multi-turn-coil-above-an-asymmetric-conductor-plate-13777
You do not need to do anything, other than to have the Coil Geometry Analysis study step in your study sequence.
Jerome Helffrich
January 16, 2019I agree with others that this is very weak as an introduction to modeling fields created by currents. For example, what other boundary conditions serve to return the currents to the wire? Another blog post said that a Perfect Magnetic Conductor boundary will do that. Is this true? If so, then does the conductivity of the boundary really matter? Could I just have a nonzero conductivity material that goes all the way around the model? Do I need ports if I am not interested in terminal measurements like impedance and power? Do I need to adjust the solver “Factor In Error Estimate” to 1e7 as recommended by this http://www.comsol.com/model/inductance-of-a-power-inductor-1250
It is ridiculous that a simple thing like modeling the magnetic field of a straight wire is not discussed in depth, because it apparently is not a simple thing to do in COMSOL.
Walter Frei
January 17, 2019 COMSOL EmployeeHello Jerome,
The question of modeling a single straight wire indeed does seem simple, but is not. The fundamental point of this article is that you cannot neglect the current return path, not in your model, and not in real life, as it does have a contribution. For a different perspective on this, see also: https://www.comsol.com/blogs/computing-the-inductance-of-a-wire/
Or, put another way: Consider a single loop of wire and find the expression for its inductance. Now, divide this inductance by the perimeter, and take the limit the radius of the loop goes to infinity (thereby approaching the case of a straight wire.) Does it converge?
Regarding the technical blogs, these are meant to be short articles which can address a single, narrow, topic. This article in particular was written solely to address a common conceptual misunderstanding. View these blogs as a supplement to the documentation, examples, textbooks, and other educational resources, as well as the COMSOL Support Services.
Barzan Tabei
June 14, 2019Hello,
I have a question about loss/current calculation of a single turn. I calculated current in COMSOL 5.3a, and everything was correct. Now, when I run my models in version 5.4, I see the same results, but when I draw it in version 5.4, I see some wired results. For example, the current’s unit is A*m in the new version while in the old one it was A. plus, the calculated value in the new model is totally different that I couldn’t figure out why. My model is as follows:
I modeled a single turn using 2D-axisymmetric modeling in ACDC (magnetic field), and I selected 1A current by coil modeling (Coil Excitation: Current). For calculating current of the cross-section (It must be 1A as I selected the coil modeling), I choose surface integration and (Magnetic fields, currents and charge, Current density-A/m2, mf.Jphi-Current density, phi component). The units and values of the versions 5.3a and 5.4 are different as I explained above. Everything in both versions was the same.
I appreciate it if anyone can help me.
Best Regards
Barzan
Barzan Tabei
June 24, 2019Solved,
thanks
Bing Zhang
July 6, 2020Thanks for the blog. Simple and very useful.
Balaji Subramanian
September 21, 2020Hi Mr. Walter Frei,
I am modeling an infinite long PCB Cu Trace in Comsol 5.3 b student version.
Task: I am trying to see a differential magnetic flux between two current carrying PCB Cu Traces having currents in opposite directions.
I am trying to simulate a situation where a differential current of 20 mA falls on a soft iron piece ( 0.4 x 0.1 mm – length and height) place just above it at a distance say 4 mm along central axis of these current carrying traces.
Doubt: How do I do this in pure 2D simulation ? I am using a rectangle geometry for the Cu traces placed one above another with a small 0.2 mm distance between them .
For return path of current I place two similar (duplicate) rectangular Cu traces at around 250 – 300 mm away from the primary traces.
I just wish to know whether I am modeling correctly for assuming an infinitely long rectangular Cu trace , carrying a +1 A or 10 A current in one direction and the latter carrying -0.998 or -9.998 A. For simulating a 20 mA differential current and seeing the magnetic flux it produces on a Soft Iron piece placed just above these conductors.
Please help me or let me know where or how I can contact you personally over Comsol website to have you check my model once.
Few things are confidential in the model hence I will be able to send you through email only.
Thanking You ,
Balaji Subramanian
Carlos Azcarraga
April 29, 2021Hello! is it possible to model in 2D the series connection of many coils? I mind, lets imagine a coil 1 an a coil 2. I asume that current enters in end 1 of coil 1 (entering to the plane). Current comes out from end 2 of coil one (out form the plane). How can I connect end 2 of coil 1 to end 1 of coil 2 to simulate a serie connection of coil 1 with coil 2? Thanks!
Walter Frei
April 29, 2021 COMSOL EmployeeHello Carlos,
Regarding the modeling of coils, please see also this more recent and more comprehensive resource:
https://www.comsol.com/support/learning-center/article/Introduction-to-Modeling-Electromagnetic-Coils-8251/112
Best Regards,
Walter Frei
March 4, 2022 COMSOL EmployeeRegarding coil modeling, see also this new blog on yet another approach that you can follow: https://www.comsol.com/blogs/computing-and-using-partial-inductance-with-comsol/