Flow through porous materials occurs on all length scales, from large-scale geological areas to nanoscale structures. Many applications are already covered by Darcy’s law, but especially in industrial applications the relation between the velocity field and the pressure gradient is no longer linear and Darcy’s law does not provide accurate results. In this blog post, we take a closer look at different flow regimes that can occur in a porous medium and how to describe them.
Modeling Flow in Porous Media on the Microscopic Scale
For a better understanding of what characterizes flow through a porous material, it is worth taking a closer look at the detailed structure. This not only gives us a deeper understanding but also gives us confidence in using macroscopic approaches to simulate flow in porous materials.
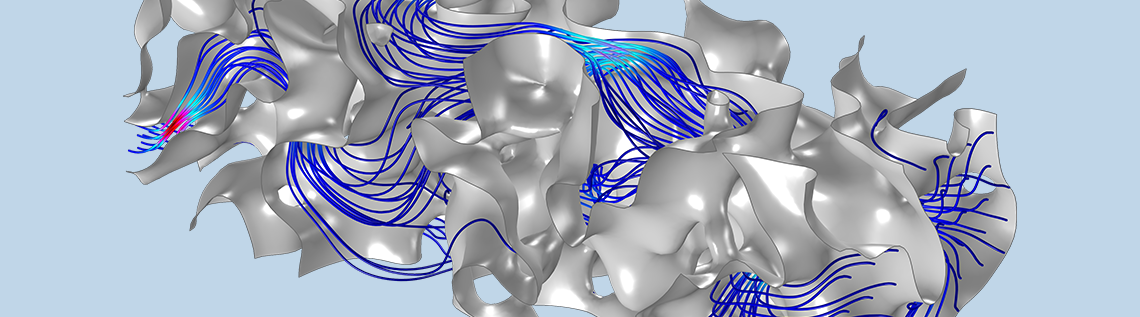
The following animation shows a complex porous structure of size 2 cm × 2 cm × 6 cm, and the flow pattern, calculated with the Navier–Stokes equation, within.
Flow pattern in a small porous block.
There are zones with low and high flow velocities, and there are also zones where flow does not occur at all. Even if the structure is irregular, the characteristic is the same when zooming to another position in the same porous sample. Accordingly, this is called a representative elementary volume (REV). Averaging over an REV gives us the macroscopic equations, as described in the next section.
To characterize the flow and obtain information about the macroscopic equations, the following values are of interest:
- Porosity \epsilon_p=\frac{V_\textrm{pore}}{V_\textrm{tot}}, which describes the ratio of pore volume over total volume and can be calculated from the geometry
- Pressure drop \Delta p/L along the flow direction (lengthwise), which can be calculated or predefined
- Superficial velocity u=\frac{Q}{A}, or the volumetric flow rate through the structure Q (m3/s), divided by the total cross-sectional area A (m2)
Flow on the Macroscopic Scale
The basic law that describes the flow in porous materials is Darcy’s law, which was first an empirical law and later theoretically derived from the Navier–Stokes equation. It describes a linear relationship between the velocity field \mathbf{u} (m/s) and the gradient of the pressure p (Pa).
(1)
with \kappa (m2) the permeability of the porous medium and \mu (Pa·s) the dynamic viscosity of the fluid, respectively.
In regular structures, like packed beds or granular soils, the permeability can be derived from the Kozeny–Carman relationship
(2)
Here, d_\textrm{p} (m) represents an effective particle diameter (for spherical particles, this is equal to the sphere diameter).
Linear Darcy’s law is valid for low velocities. Just as with free flows, the Reynolds number in porous media
(3)
is also used to characterize flows, with L (m) being a characteristic length scale.
Linear Darcy’s law is valid for about Re<10. Then the pore-scale flow can be described as creeping flow, where the inertial forces are very small as compared to viscous forces. This is the case for groundwater flow and other low-velocity and/or high-viscosity applications. However, in most industrial applications, such as in packed bed reactors, filters, or even food products, far higher velocities are involved. This is also the case for gas flow where the viscosity is very low. In such cases, Eq. 1 is not sufficient, and nonlinear terms must be introduced. This is referred to as non-Darcian flow, which can be formulated as follows:
You can immediately see that the left term on the right side of the equation corresponds to Darcy’s law. For the nonlinear term, the Forchheimer equation suggests that
(4)
with \beta being the inertial resistance coefficient and c_F the Forchheimer (dimensionless) parameter.
In the case of packed beds, the Ergun equation is very useful. Here, the following relationships are used:
(5)
At high Reynolds numbers, viscous effects are small compared to inertial effects and the nonlinear term in the Ergun equation is dominant, which is known as the Burke–Plummer equation.
The equations are already quite descriptive, but it is even better to visualize the entire whole in a graph. To do so, let us take a look at the dependence of the velocity on the pressure drop in a packed bed with an average particle diameter of d_p=0.1 (mm). Kozeny–Carman describes the linear limit and Burke–Plummer the quadratic limit. Both the Ergun and Forchheimer equations can cover the linear and quadratic regimes. The difference between both is the calculation of the permeability according to Eq. 2 or Eq. 5.

Comparison of the Kozeny–Carman, Forchheimer, Ergun, and Burke–Plummer relationships.
A non-Darcian law of quite a different kind — therefore, excluded from the above consideration — deals with the particularities of gas flows where the mean free path of the gas molecules is about the same size as the pore dimension. In this case, the collision of gas molecules with the walls of the pore channels happen more often than the collisions with other gas molecules. This is the so-called slip flow regime, and typical applications range from nanomaterials to gas reservoir modeling. The permeability relationship in this case is
(6)
where p_\textrm{A} is the absolute pressure (Pa) and \kappa_\infty is the permeability (m2) under high pressure, where the molecule collisions with the walls are negligible compared to collisions among each other.
The Klinkenberg parameter b_\textrm{K} (Pa) depends on the porous medium’s permeability, and you can find b_\textrm{K}\propto\kappa_\infty^{-0.36} (Ref. 1).
All of the aforementioned permeability models are available with the Porous Media Flow Module. The Forchheimer and Kozeny–Carman equations are also available with other modules that support flow in porous media.

Where to find the permeability relationships.
Non-Darcian Flow, from Microscopic to Macroscopic Scales
How can we connect both approaches? The first model — the REV — gives us the dependency of the velocity on the pressure gradient, and we can also determine the porosity and permeability. We look at the flow behavior over several orders of magnitude for the pressure drop; similar to above. The simulation of the pore structure is relatively expensive in terms of computational cost, due to the complex structure, which has to be resolved properly. In addition, the Navier–Stokes equation itself is more complex as to the averaged equations (Eq. 2–Eq. 6).
The macroscopic approaches are very good approximations. Darcy’s law is suitable for small pressure drops and low velocities, whereas Burke–Plummer is suitable for large pressure drops and high velocities.
The Forchheimer equation can approximate the transition region very well. In this example, the Forchheimer equation was fitted to the data from the microscopic model to obtain the Forchheimer parameter c_\textrm{F}, which is usually determined in laboratory experiments.
Final Remarks
In this blog post, we looked at the flow in porous media at microscopic and macroscopic levels, and showed that the macroscopic approaches are a very good approximation — in the respective areas of validity.
An example for the simulation of industrial applications with the Forchheimer equation is a model of a porous microchannel heat sink.
After discussing the flow through porous media, we will discuss heat transfer in porous media in an upcoming blog post.
Try It Yourself
Try the tutorial model featured in this blog post by clicking the button below. Doing so will take you to the Application Gallery, where you can download the MPH file.
References
- Y. Wu, K. Pruess, and P. Persoff, “Gas Flow in Porous Media With Klinkenberg Effects“, Transport in Porous Media, vol. 32, pp. 117–137, 1998.
- J. Bear, Dynamics of Fluids in Porous Media, Courier Corporation, 1988.



Comments (6)
Paolo Canu
March 15, 2020Hi Nancy,
thanks for the interesting contribution.
The results of the last figure require specifying a particle diameter for all the macroscopic models, which is not obvious what it means in the foam structure simulated by NS.
Is there any rule to suggest ‘an equivalente dp’ from the foam structure or it just becomes an adaptive parameters?
Regards,
Paolo
Nancy Bannach
March 16, 2020 COMSOL EmployeeHi Paolo,
that is a good question. The average pore diameter is often used. However, several factors do play a role, such as how well the pores are connected. In this example the parameters were determined by curve fitting. The dependence of the velocity on the pressure drop is known from the REV model and the parameters can then be fitted to this solution, similar to the following model from our application gallery:
https://www.comsol.com/model/mooney-rivlin-curve-fit-5886
Alternatively, the parameters can also be determined using a parametric sweep which is computationally more expensive.
I hope this answers your question.
Best regards,
Nancy
ali ayachi omar
May 28, 2020Hi Nancy, I’m interested in how to get the microstructure and the porous layer design.
Nancy Bannach
May 29, 2020 COMSOL EmployeeDear Ali,
the geometry was artificially created. The details are too extensive, but roughly summarized: A random solution is generated, e.g. by applying a diffusion equation to a random initial distribution of the concentration and applying a filter data set to this solution from which a geometry or mesh can be generated.
I hope this answers your question, otherwise contact our support team to elaborate on this in detail.
Best regards,
Nancy
Abdur Siddiq
January 25, 2023Hi Nancy,
Thank you for your work on this blog. I am a new learner.
I checked the file provided, and it looks like the streamline flows inside the structure, not the voids between porous struts.
Is that not affecting the measurement? Do you have any resource about Fluid Solid Interaction ? I’d like to simulate water through the porous structure like you have here, but the water filled the empty space (I assume water will be a moving mesh) .
If I want to have the streamline flows between the structure, what elements that I need to change?
With mm scale unit, how long will it take to complete the computaion? I tried with a laminar flow on a porous structure, and my PC struggled trugling to get the result.
Is the mesh of free triangular, free tetrahedral and boundary layers compulsory in the simulation structure?
Many thanks,
Abdur
Nancy Bannach
January 31, 2023 COMSOL EmployeeDear Abdur,
The flow is inside the modeling domain and the modeling domain represents the voids of the porous material. The solid material is not a modeling domain in this case and therefore is not included here. The mesh is optimized for fluid flow simulations and boundary layers are practically essential to resolve the region close to the wall properly.
Since you are a a new learner, I recommend that you start with our introductory course at https://www.comsol.com/learning-center. Then you can find more models in our application gallery https://www.comsol.com/models – just search for specific topics and applications and I’m sure you find something useful. If you still need assistance or want to discuss your simulation task in more detail, I recommend to contact our support team via https://www.comsol.com/support.
Kind regards,
Nancy