
Today, guest blogger Linus Fagerberg of Lightness by Design, a COMSOL Certified Consultant, shares how multiphysics simulation provides accuracy in automotive muffler design.
The acoustic design of mufflers in the automotive industry has traditionally been performed by an iterative process where different alternatives are compared by experimental methods until a satisfactory design is found. Numerical simulation can drastically reduce a project’s time and expenses, while simultaneously increasing the performance of the muffler.
Studying Acoustics and Structural Mechanics in a Muffler Design
Sweden-based Scania has utilized the benefits of numerical simulation for a long time and is constantly improving their modeling knowledge and skill set. Recently, Lightness by Design began working with Scania to evaluate the benefits of using a multiphysics simulation approach where acoustics are coupled to shell structural mechanics in the muffler design process.
Together, we found that introducing structural mechanics into an acoustic model can have a large impact on the predicted muffler characteristics. The differences can also, to some degree, explain previous discrepancies between a simulation and experimental results, where structural mechanics obviously had always been present but never taken into account.

The exhaust system for an automotive muffler.
We’ll use the classic COMSOL Multiphysics model of an automotive muffler as an example to illustrate the effect of including structural mechanics in a normal pressure acoustic simulation. The model is available in the Application Gallery and is modified by including shell physics and a multiphysics coupling.
Setting Up the Multiphysics Model
The model, shown below, is solved for the following boundary constraints: Plane wave propagation is defined on both the inlet and outlet surfaces, with an incident pressure of 1 Pa applied at the inlet. All walls, interior and exterior, are defined as sound hard barriers or shells made of steel (E = 210 GPa, ν = 0.3, ρ = 7800 kg/m3, η = 0.02, and t = 1 mm) in the Pressure Acoustics node. We also define the shell physics and restrict all degrees of freedom to zero at the inlet and outlet edges. In the image below, you can see the surfaces defined as shells in darker blue.
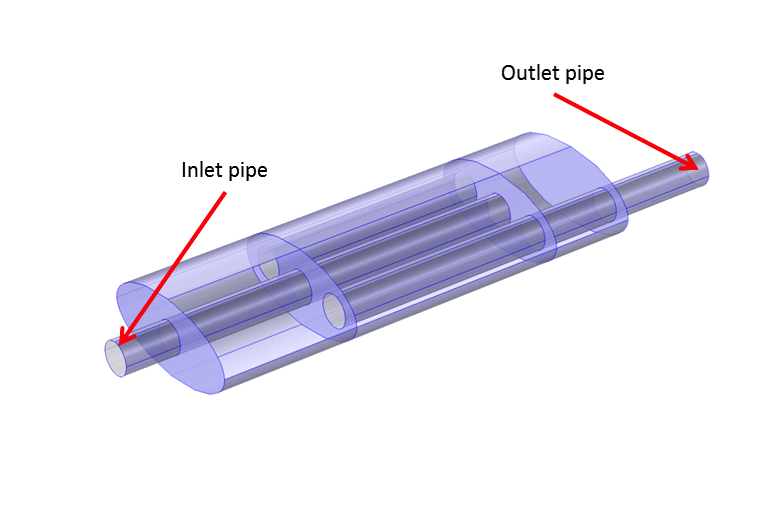
The Automotive Muffler model with inlet, outlet, and highlighted shell boundaries.
The actual multiphysics coupling is defined at the interface between the shells and the acoustic domain. This couples the pressure variable, p, which is solved for in the Pressure Acoustics node, and the nodal displacements, (u,v,w), which are solved for in the Shell physics node, according to
where n is the surface normal vector, \rho is the air density, \nabla is the Laplace operator, p_\textrm{t} is the total acoustic pressure, u is the shell surface displacement vector, and t represents time.
The condition represents continuity in normal acceleration. The multiphysics coupling Acoustic-Structure Boundary is predefined and located under the Multiphysics node in the model tree. See the image below for the final setup in the model tree.
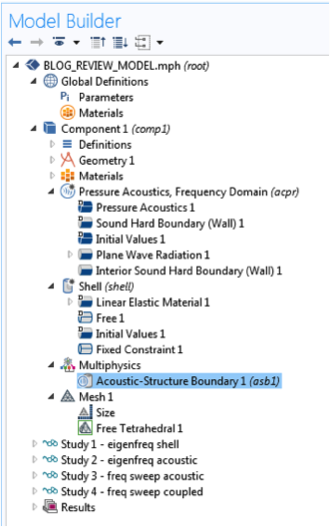
The model tree with Pressure Acoustics, Shell, and Multiphysics nodes.
A free tetrahedral mesh with eight second-order elements per wavelength at maximum frequency is used, yielding the maximum element size
where c is the speed of sound in air (343 m/s), fmax is the highest frequency of interest (800 Hz), and nmin is the set number of elements per wavelength (eight in this case).
The transmission loss is finally calculated as
where P_{in} and P_{out} are the acoustic power at the muffler inlet and outlet, respectively, calculated as
where A_{in} and A_{out} are the inlet and outlet areas, respectively; p_{in} and p_{out} are the inlet and outlet acoustic pressure, respectively; \rho is the density of air; and c is the speed of sound in air.
Then, we solve the model; first for the eigenfrequencies and later by carrying out a parametric sweep in the frequency domain (10 to 800 Hz in 2 Hz increments).
Results for Coupled Physics in the Muffler Design
The effect on the predicted transmission loss for the muffler, modeled with pure pressure acoustics, is compared to the multiphysics model in the image below. Looking at the calculated transmission loss, you can see that the curves are quite similar with small discrepancies, except for the frequency region between approximately 600 to 670 Hz. The behavior of the transmission loss in this region is similar with and without coupled shell physics, but we can see a large amplitude difference.
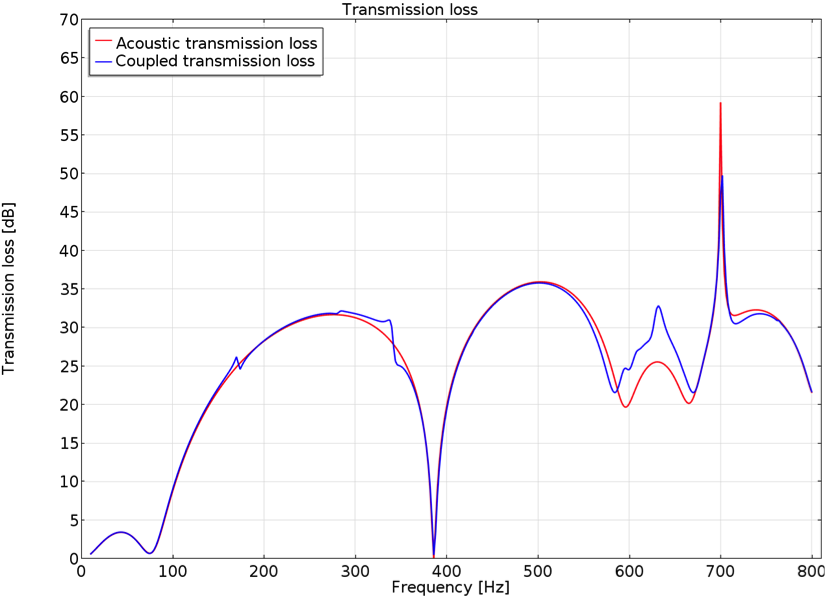
A transmission loss comparison between pure acoustics and multiphysics models.
This amplitude difference can be explained by the interaction at the interface between the encapsulated air mass and the shell structure. The mechanism behind this structure can be further explored by eigenfrequency analysis.
In the graph below, the eigenfrequencies are plotted against frequency and interesting eigenfrequencies are identified in the transmission loss diagram. Two calculated cases are presented: pressure acoustic physics only, yielding the frequencies where standing waves occur in the air mass, and shell physics only, yielding the frequencies where the structure is easily excited into vibration. This chart gives the possibility to detect coinciding eigenfrequencies in the exciting load (standing waves in the air mass) and the encapsulating structure.
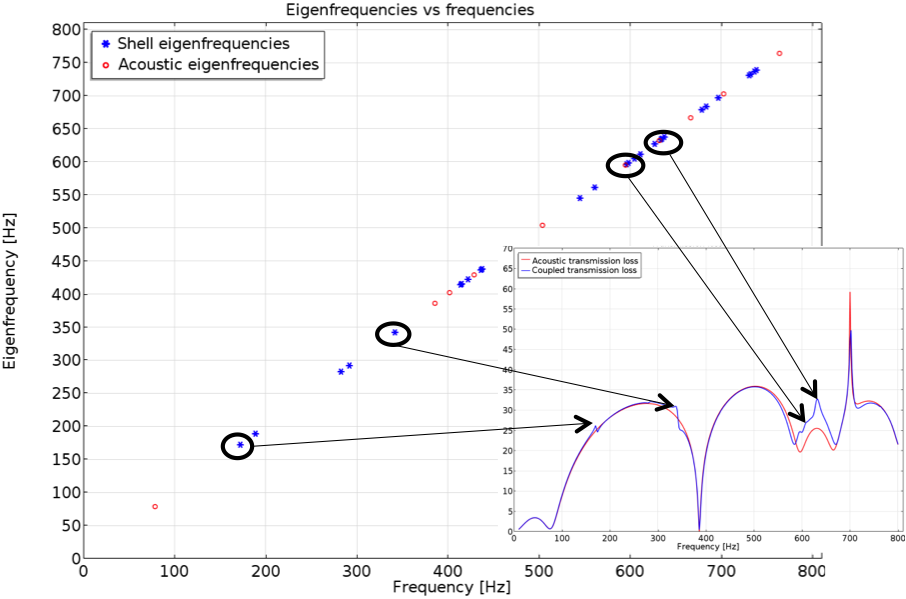
Transmission loss and eigenfrequencies for both models.
There are at least three regions where the predicted transmission loss differs between the pure acoustics and multiphysics models. These are around 170 and 340 Hz and the entire region between 570 and 670 Hz. The first two frequencies (170 and 340 Hz) are pure shell modes that can be excited by the pressure pulses without acoustic resonance occurring; i.e., no coinciding eigenfrequencies are needed.
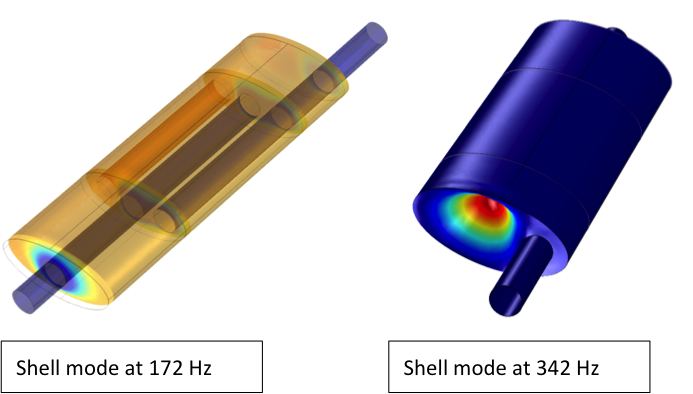
The shell mode shapes at eigenfrequencies of 172 Hz and 342 Hz.
A group of closely spaced eigenfrequencies, both acoustic and shell modes, is found around 600 Hz and 634 Hz. This is right in the region where the largest differences in the transmission loss occur. Let’s have a look at what is happening at the multiphysics interface at 634 Hz, since this is where the difference in transmission loss is the greatest.
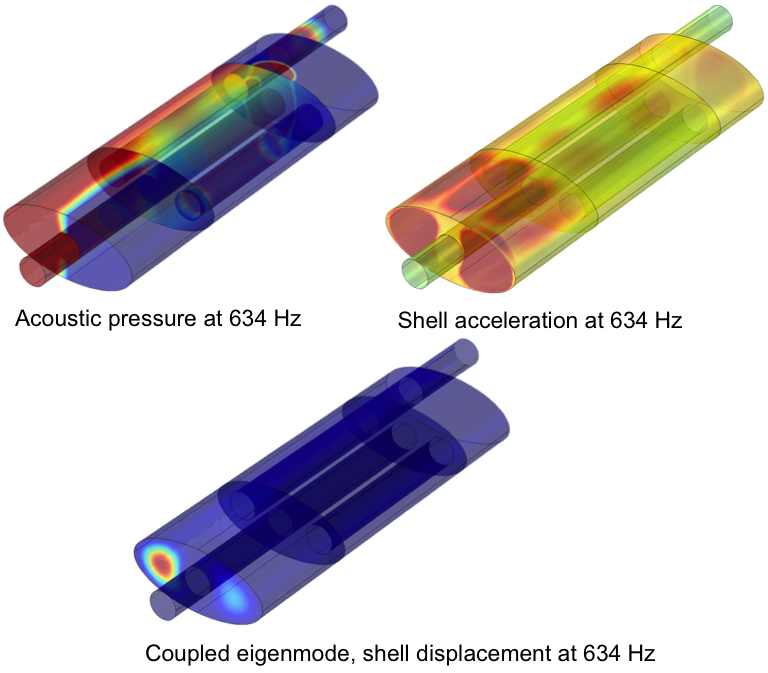
The acoustic standing wave and shell mode shape at eigenfrequencies at 634 Hz.
We are looking at an eigenmode where the shell is easily excited into vibration, which corresponds very well with the pressure mode when excited at 634 Hz. This causes high acceleration levels at the shell end plates. This interaction effect is most likely causing the difference in transmission loss.
Normally, an increased transmission loss is beneficial for a muffler, but if it comes at the price of a vibrating structure, it could be questionable both from a fatigue and shell noise standpoint. Whether the shell vibrations at the excited eigenmodes pose a problem or not is mostly dependent on the amplitude of the vibrations. If there are large pressure amplitudes, they can give rise to both noticeable shell noise as well as structural strains with increased risk for fatigue problems.
The endplate modes at 170 and 340 Hz could be easily removed if necessary by increasing the endplate thickness with only a small associated weight penalty. These two modes are excited by the incident pressure, since no standing wave in the air mass exists at these frequencies. Hence, the severity of these modes can be estimated by comparing the predicted operating frequencies and pressure amplitudes of the muffler with the resonating shell frequencies.
The third example mode, at 634 Hz, where the largest difference in transmission loss occurs, is more complex to examine using simulation only. This study would require some experimental evaluation where the amplitudes of the system can be measured. This is mostly because of the broad frequency range (570 to 670 Hz) and the combination of both acoustic and shell modes. The acoustic modes change the pressure distribution and can locally increase the acoustic pressure. Hence, noticeable vibrations and possible fatigue problems could arise.
Concluding Thoughts on Using Multiphysics Simulation for Acoustic Muffler Design
When designing automotive mufflers, numerical simulation with COMSOL Multiphysics results in better products, while simultaneously reducing the risk and cost of the project and the end product’s time-to-market. With the implementation of a multiphysics coupling for acoustics and structural mechanics, new possibilities for increasing the efficiency of the design phase and the reliability of the simulation results are opening up.
As seen with market leader Scania, keeping the leading edge requires continuously honing skills and utilizing advances in simulation technology. This organization keeps developing their knowledge with the help of their work with COMSOL Multiphysics and COMSOL Certified Consultant Lightness by Design.
Get Started Simulating Your Own Muffler Designs
Download one of the following example models or applications to see how you can use multiphysics simulation to optimize your own automotive muffler design:
- Automotive Muffler
- Absorptive Muffler
- Eigenmodes in a Muffler
- Absorptive Muffler Designer
- Absorptive Muffler with Shells
About the Guest Author
Linus Fagerberg from Lightness by Design is an experienced consultant working with simulation-supported product development. He holds a PhD from KTH Royal Institute of Technology and is specialized in the structural mechanics of composites, stability, and optimization. Linus believes that numerical simulation is a great tool to consistently deliver high-quality products, improve performance, and mitigate risks. Lightness by Design is a COMSOL Certified Consultant based in Stockholm, Sweden.




Comments (0)