
Safe and cost-effective drilling is a major issue in the oil and gas industry. In addition to the common prospecting risk, the borehole itself provides uncertainties that are not desired, but unavoidable. Today, we would like to show how numerical simulations can help here. The goal is to predict the stability of an open-hole multilateral well for deciding if the well will need expensive mechanical stabilization — or not.
Multilateral Drilling
The development of drilling techniques during the last century provides the capability of spreading wells into several branches, among other investigations. This enhanced method allows a much wider reservoir area to be covered, either for oil and gas or for geothermal energy production.
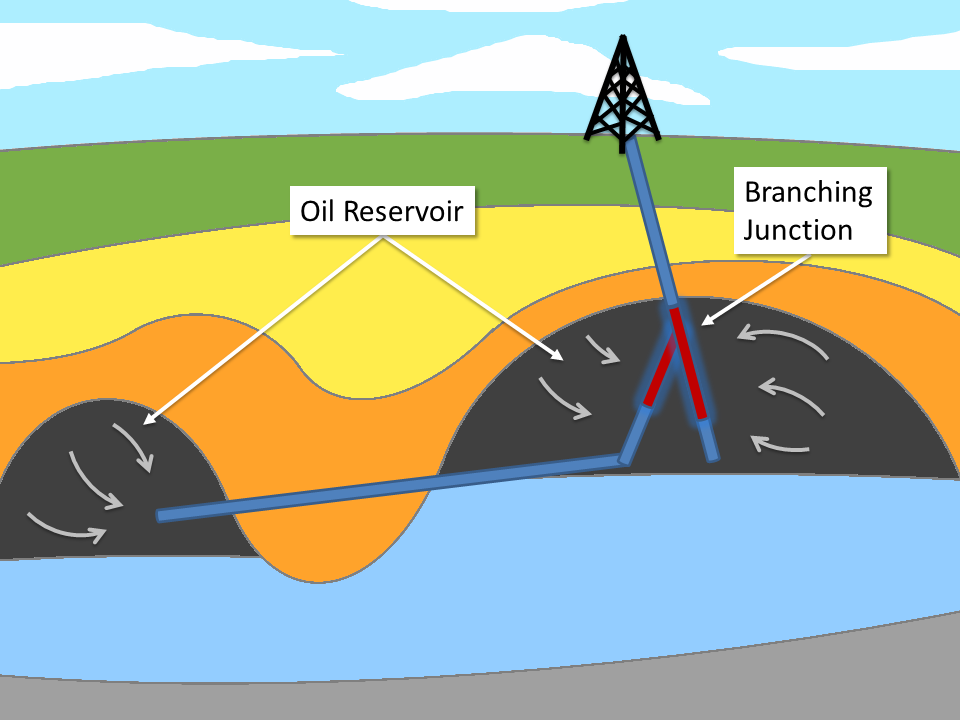
Natural resource recovery: Oil is produced from a natural reservoir via mechanical pumps that raise the oil to the surface. A side-branch of the drilling reaches into an adjacent reservoir by a junction.
However, branching junctions are also less stable than single boreholes and have to be stabilized with a liner or casing quite often. Even if the borehole would stay open by itself after a drilling procedure is completed, it undergoes additional stress when the production process is engaged by starting pumping through the wellhole. Borehole casing is very expensive, it adds significantly to the overall cost for a drilling project. If possible, one would rather avoid the deployment of additional mechanical stabilization.
The question is: Is the open borehole stable without casing?
Modeling Open-Hole Multilateral Wells
A chain is only as strong as its weakest link. To answer the question of stability, it is sufficient to reduce the investigation to the most critical point: the branching junction (or one of the junctions, if there are more branches). If the well is stable here, we may assume that it will hold up everywhere else. As a first approach, we assume only elastic deformation. Thus, all we need to build the model is the Subsurface Flow Module and the Solid Mechanics physics interface in COMSOL Multiphysics.
There is no need to take the fluid flow within the well into account. All we need to know is the pressure level at the well boundaries. This is prescribed by the pump and the depth of the junction. Also, the local symmetry of the part of interest allows us to reduce the geometry to one half and apply symmetry boundary conditions.
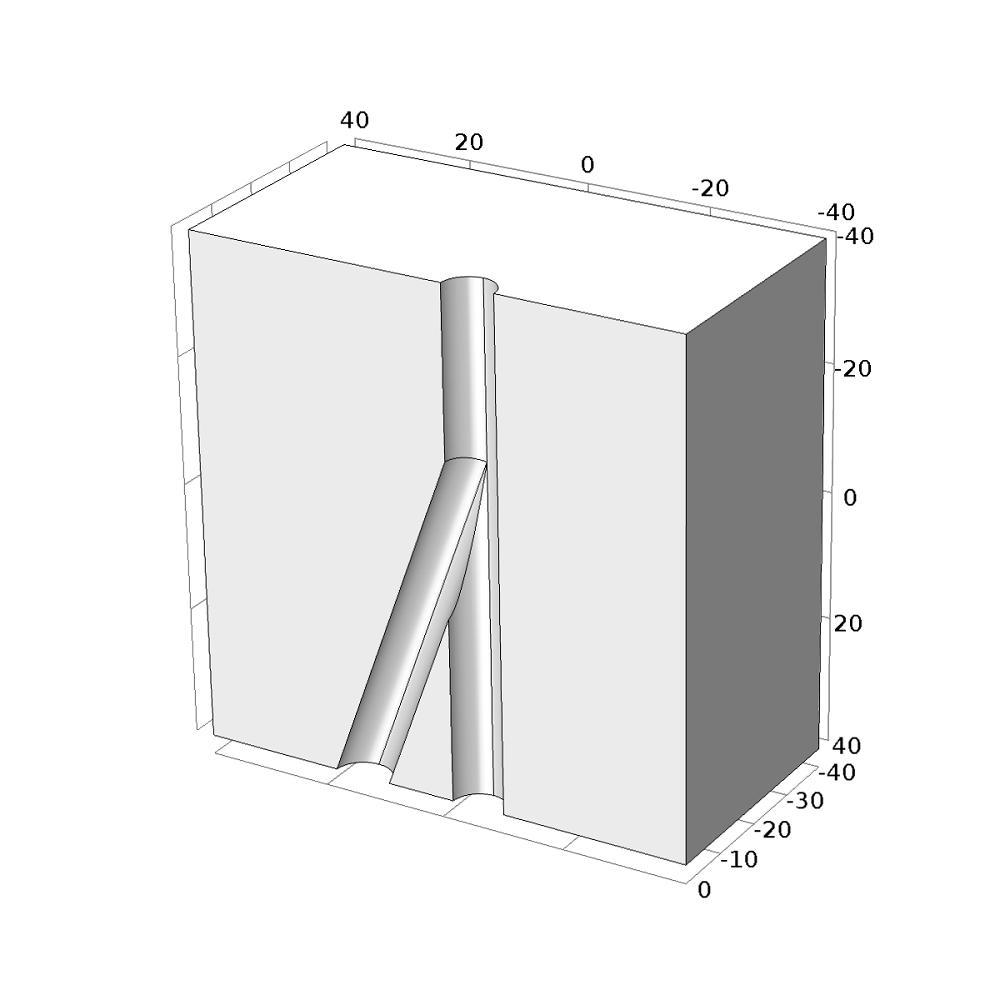
Model geometry of the multilateral well branching junction. Due to symmetry, only one half of the junction needs to be considered.
Physical Formulation
The subsurface flow within a porous media reservoir can be described by a combination of Darcy’s Law and a continuity equation:
with the permeability, \kappa, the dynamic viscosity, \mu, and the oil pore pressure, p_f. The pressure in the pores will change when the production process starts; a lower pressure at the walls of the well due to pumping leads to flow in the pores and a pore pressure drop.
Changes in the pressure load effect a deformation because the Cauchy stress tensor, \sigma, is related to p_f:
with the elasticity matrix \boldsymbol{C}=\boldsymbol{C}(E,\nu), which depends on Young’s modulus, E, and Poisson’s ratio, \nu, the strain tensor, \epsilon and the Biot-Willis coefficient, \alpha_B. This relation couples the fluid flow with the equation for the quasistatic deformation
where \boldsymbol{F} denotes any external body forces.
Boundary Conditions and Model Data
The only exit for the oil is the well. Thus, the boundaries perpendicular to the well axis (top and bottom) are assumed to provide No Flow conditions. As I mentioned above, the symmetry face provides symmetry conditions in both the flow and mechanical interfaces. The model constrains movement at all external boundaries, while the well opening is free to deform.
| Variable | Description |
Value |
|---|---|---|
| \rho_f | Fluid density |
0.0361 lb/in3 |
| \rho_s | Solids density |
0.0861 lb/in3 |
| \mu | Fluid dynamic viscosity |
1·10-7 psi·s |
| \kappa | Permeability |
1·10-13 in2 |
| E | Young’s modulus |
0.43·106 psi |
| \nu | Poisson’s ratio |
0.16 |
| p_r | Reservoir pressure |
122.45 psi |
| p_w | Well pressure |
0 psi |
Model properties.
Results
To get an impression of the results, let’s have a look at a re-mirrored result plot showing the total displacement due to the pressure drop and the resulting velocity field. So far, we know that the most critical part seems to be the area right above the branching. But we still do not know if the well is stable.
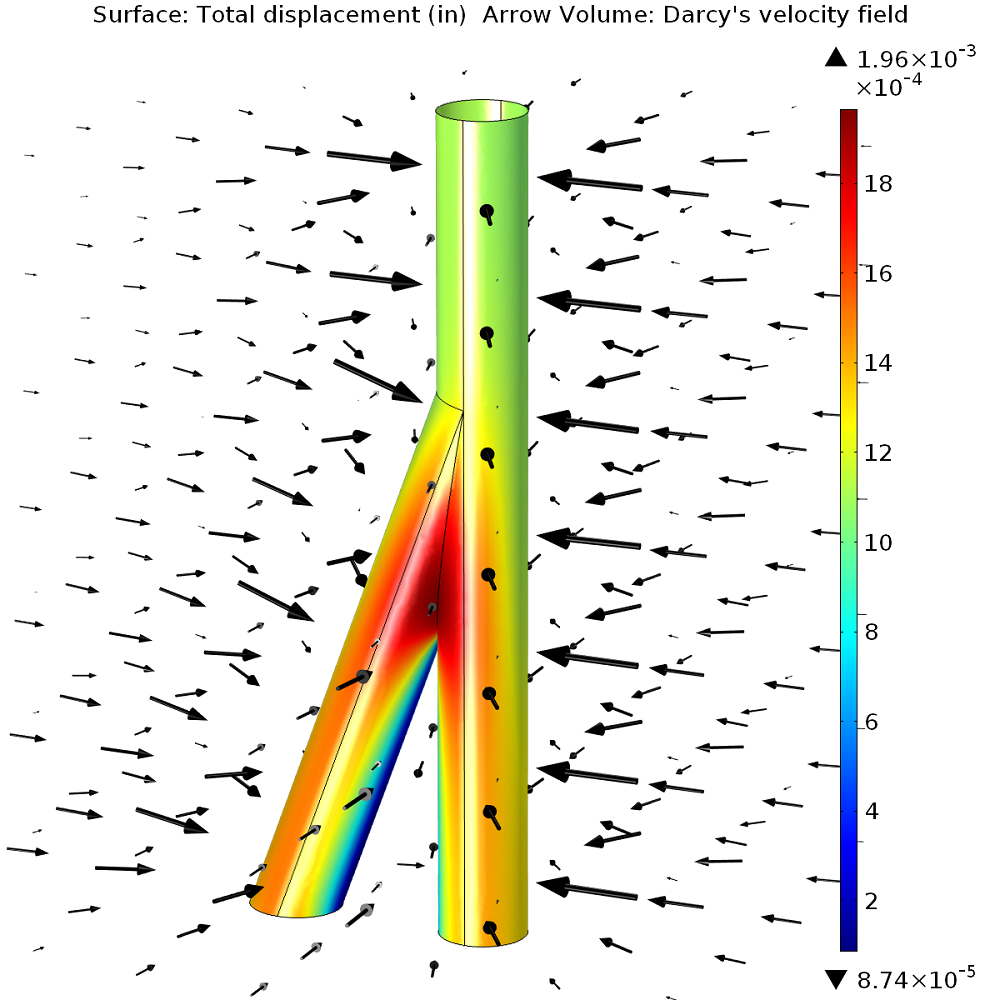
Surface displacement (color plot) and velocity field (arrow plot) of the branching junction.
Criterion for Well Stability
The results of the model show how the pressure change affects the stress and strain distribution around the well. To find out if the hole is stable or not, we need a failure criterion. The 3D Coulomb criterion (a linearized form of the Lade criterion) reproduces the laboratory data of rock failure experiments well, but note that it requires calibration data.
The criterion relates rock failure, the three principal stresses (\sigma_1, \sigma_2, and \sigma_3), and the fluid pressures as follows:
where
with the Coulomb cohesion, S_0, and the Coulomb friction angle, \phi. For different results of the function, various scenarios can be expected: fail > 0 predicts stability; fail = 0 indicates the onset of rock failure; and fail < 0 denotes catastrophic failure.
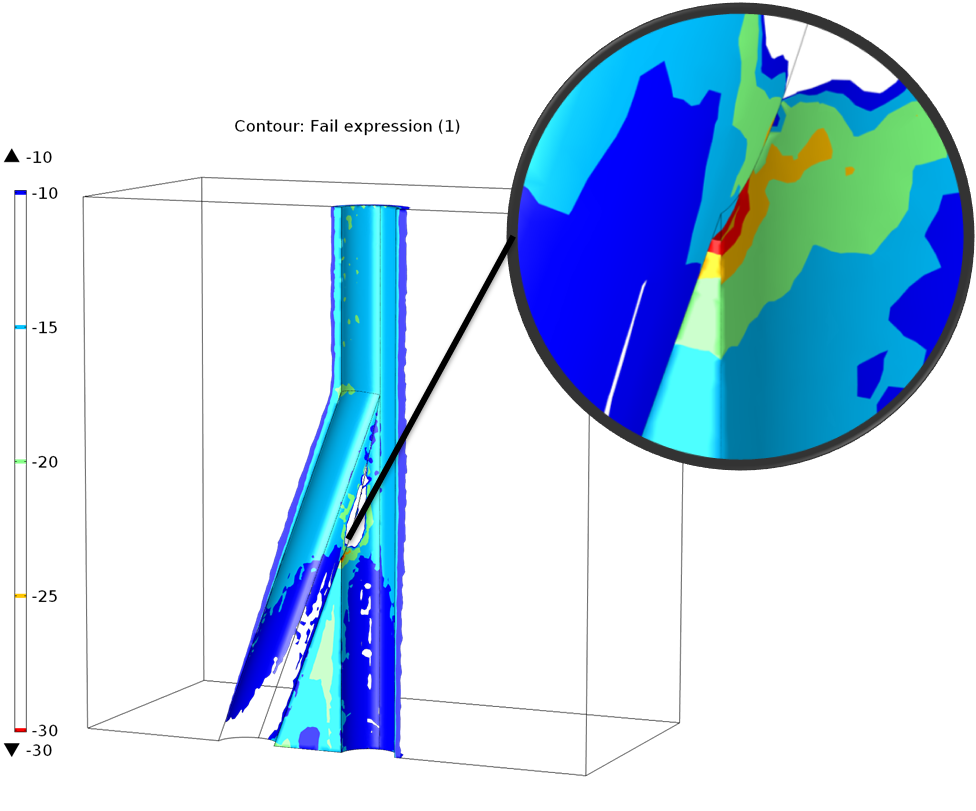
Evaluation of the fail function (equation anchor: failure). The highest potential for failure is right above the branching.
When the fail values become increasingly negative, the potential for failure is higher. As expected, the fail function estimates show the greatest potential for failure just above the branching in the well. The failure potential can be reduced by adding a support force, e.g., a casing.
Below, you can see the results of a parametric sweep study. With increasing well support force, the failure potential decreases.
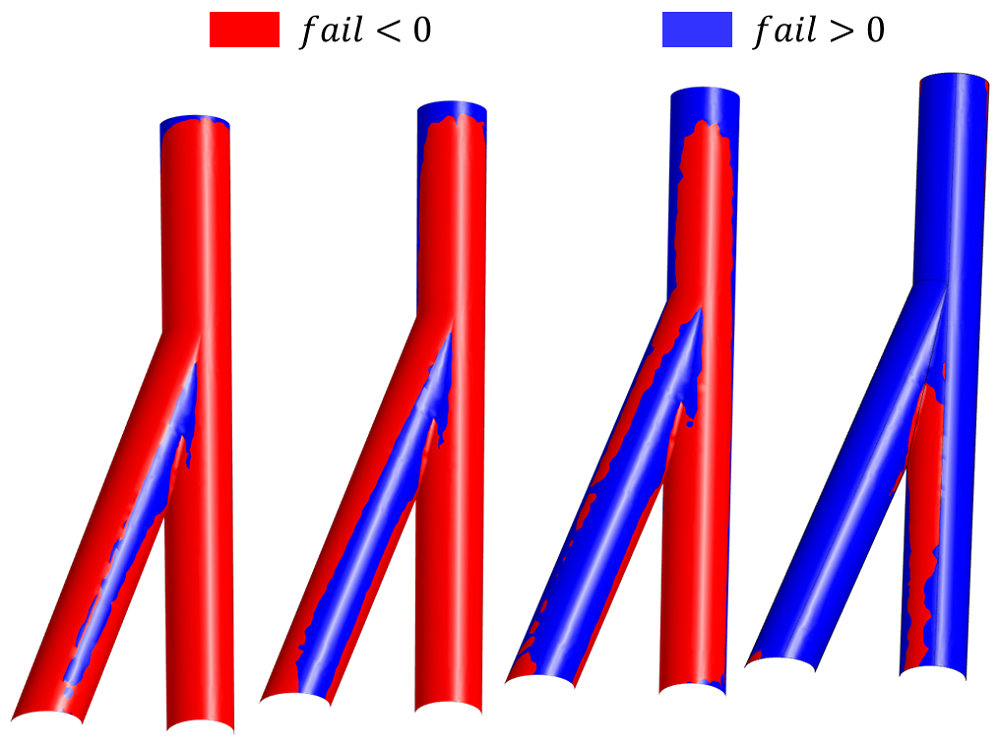
Evaluation of the fail function for different well support forces from a parameter study (support force from left to right: 5e4, 7.5e4, 1e5, 2.5 N/m^2).
Conclusion and Further Modeling Opportunities
Here, we have showed you how to model a branching junction of an open-hole multilateral well. As the stability of open wells is an essential piece of information, this model is a good example of how numerical simulations can significantly save money. The important estimation of stability can be clarified in the early project phase.
The presented approach focuses on elastic deformation, while related analyses can also be conducted for elasto-plastic materials, for example. These are automated in the Geomechanics Module and in the Structural Mechanics Module. This model could also easily be expanded to study the influence of temperature by adding thermal expansion. This would be especially of interest for studies concerning geothermal energy approaches.




Comments (0)