I love trees and my favorite is definitely the ficus, all varieties included. A few weeks ago I had the chance to admire a stately ficus microcarpa (see figure below). What struck me above all were its aerial roots. Roots are designed to absorb water and nutrients, sustaining the tree and synthesizing substances responsible for its growth. A thought crossed my mind right away: the shape of those roots and the way they coalesce have surely been optimized by Mother Nature.

|

|
Ficus microcarpa: overview (left), aerial roots detail (right). Pictures taken in Naples, FL, USA.
Upward Transport of Substances in Tree Roots
The upward transport of water and nutrients is mainly due to phenomena like capillary pressure and osmosis. This means that we are dealing with a fluid dynamics problem; the fluid is flowing because of a pressure difference between two points. So nature has to solve the following problem: given a certain pressure difference, what root distribution would maximize the flow rate and synthesis rate of nutrients? That problem further reminds me of a simulation with a very similar goal — the optimization of a microreactor.
Optimization of a Microreactor
In this simulation a solution is pumped through a catalytic bed, or microreactor, where a reactant undergoes chemical reaction within the porous catalyst. The simulation accounts for fluid dynamics of the solution pumped through the catalytic bed, mass transport of the reactant, and its reaction rate. The distribution of catalyst in the catalytic bed determines the total reaction rate: a large amount of catalyst results in a low flow rate through the bed while less catalyst gives a high flow rate but low conversion of the reactant. Now we need simulation to optimize our design. COMSOL Multiphysics can find an optimal catalyst distribution by maximizing the reactant conversion for a given total pressure difference across the bed. Microreactors are widely used in process engineering due to their energy efficiency, scalability, safety, and their finer degree of control. I think that you will agree that the time invested in optimizing them is well worth it.
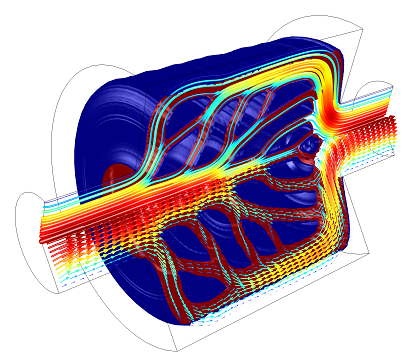
Simulation results: distribution of the porous catalyst and velocity vector field and streamlines are shown.
Optimal Distribution in Microreactors and Tree Roots
The figure above shows one of the possible optimal distributions of a porous catalyst found by COMSOL Multiphysics. To me, it resembles the aerial roots of the ficus microcarpa, and many other “nutrient distribution networks” that can be found in nature too for that matter.
We have to bow to Mother Nature: in order to mimic what she has optimized naturally over thousands of years, we need cutting-edge multiphysics simulation technology.




Comments (0)