
Guest blogger Eric Linvill of Lightness by Design shares how materials modeling provides insight into paperboard formation and bending resistance.
Formation is a fundamental physical characteristic of paper that can have profound effects on the production and performance of that paper. The finite element method can be utilized to better understand how formation affects mechanical quality control tests and their results. Using the Lorentzen & Wettre (L&W) bending resistance (15°) test, we investigate how paperboard formation affects bending resistance.
A Brief Introduction to Paper Mechanics
Paper is a quasirandom material; that is, during the production of paper, there are factors that prevent paper from becoming perfectly uniform. While on the paper machine, paper fibers orient themselves randomly in-plane (sometimes slightly out-of-plane as well), but with a preference to point in the direction of motion. These orientations are then locked in place through the press section, which removes a considerable amount of water from the pulp. This means that the final paper product becomes strongest and stiffest in approximately the in-plane direction of production (machine direction, or MD); weaker and less stiff in the in-plane direction perpendicular to MD (cross direction, or CD); and weakest and least stiff in the out-of-plane direction of the paper (z direction, or ZD).
Additionally, during production, paper fibers will tend to group together in the form of flocs. These flocs will also remain through the press section, thus resulting in a final structure that has volumes of relatively high and low density. These areas of low and high density correspond respectively to areas of low stiffness and strength versus high stiffness and strength.
Previous studies have examined the effect of formation on tensile testing and correlated the low-density areas to areas with high local deformation as measured by digital image correlation and thermography (Ref. 1). Formation is typically viewed through the use of transmitted light, as can be seen in the image below.

Formation pattern in copy paper as illuminated with transmitted light, where the light areas correspond to low-density areas and the dark areas correspond to high-density areas. Hold a piece of paper up to a light to see for yourself!
Paperboard is similar to the paper shown above, except that it is thicker and more rigid. When looking at the quality of paperboard, finite element methods can be utilized to help paper producers better understand mechanical quality control testing; converting performance; packaging performance; and spatial material variation (e.g., formation). As an example, the bending stiffness is an important material property for package performance: Paperboard with high bending stiffness tends to have greater tactile stiffness when formed into a carton than paperboard with low bending stiffness. Additionally, greater bending stiffness can contribute to a greater carton strength. Therefore, bending stiffness is oftentimes a key specification for paperboard producers and purchasers. Bending stiffness is typically measured by either the Taber method or the L&W method, but this study focuses solely on the L&W method for bending resistance up to 15° (ISO 2943).
This blog post specifically considers a three-ply folding box board (FBB), which consists of three layers of paperboard. For FBB paperboard, the outer two layers are typically stiffer, stronger, and smoother than the bulky and relatively weak inner layer. This structure is typically utilized to maximize bending stiffness and print properties while minimizing material cost. Whether or not the overall bending resistance is affected by ply formation is unknown, although one may speculate that poorer formation should cause less bending resistance. However, many of the methods with which a papermaker can improve formation require significant capital investment (e.g., installing a new headbox). Therefore, in order to make a cost–benefit analysis, the effect of formation on the bending resistance must be quantified. The following model has been created to quantify the degree to which the overall bending resistance may be affected by the formation of the top ply alone. Two aspects of formation are investigated: the magnitude of the density variations and the floc size.
Modeling an L&W Bending Resistance Test Piece
The model we use here is based on a standard L&W bending resistance test piece, which measures 38 mm in width with a test length of 50 mm, for CD bending. A three-ply construction is utilized for the paperboard in order to represent the three-ply structure of FBB: The bottom and top plies measure 100 microns, whereas the middle ply measures 200 microns.
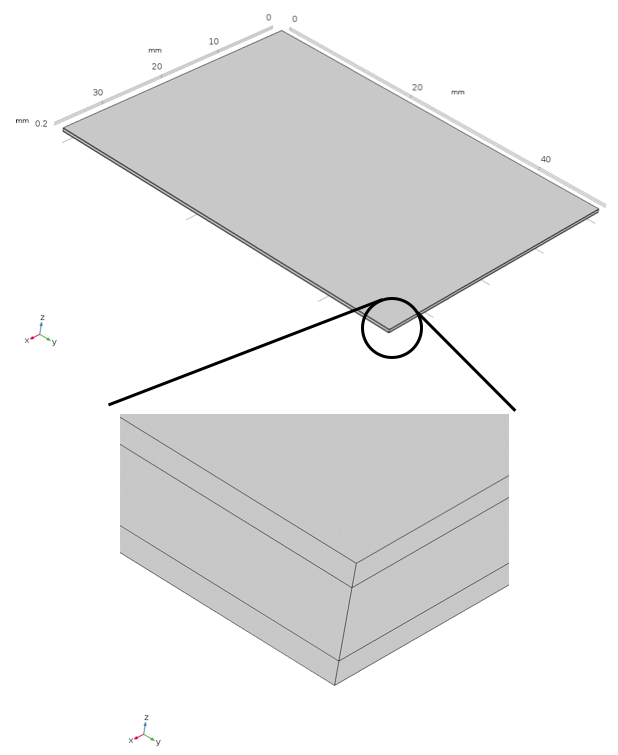
Three-layer model for an L&W bending resistance test piece.
The paperboard is fixed in one end (at y = 0), and an out-of-plane displacement is applied at the other end (at y = 50 mm) that corresponds to the 15° bending rotation during the L&W bending test. The output of the model is the resultant force at the applied deformation.
A purely elastic model is utilized, which is an oversimplification of reality, because bending up to 15° likely causes plastic deformation in the test piece. This simplification is nonetheless taken for two reasons: This model is only a demonstration, and the elastic bending stiffness is considered to be the parameter that drives carton stiffness and strength. The following table shows the average elastic material properties for each ply. Note that all material properties are fictional and do not represent an actual, commercial paperboard.
| Material Property | Top and Bottom Ply | Middle Ply |
|---|---|---|
| MD elastic modulus (MPa) | 4000.00 | 2000.00 |
| CD elastic modulus (MPa) | 2000.00 | 1000.00 |
| ZD elastic modulus (MPa) | 250.00 | 100.00 |
| In-plane (MD-CD) Poisson’s ratio | 0.45 | 0.45 |
| Out-of-plane Poisson’s ratios | 0.00 | 0.00 |
| In-plane (MD-CD) shear modulus (MPa) | 1400.00 | 700.00 |
| Out-of-plane shear moduli (MPa) | 60.00 | 30.00 |
Table 1. Material properties for the different plies.
The method to apply random variations to a material model is relatively easy (especially in comparison with other commercial structural finite element software) and is described step-by-step in a blog post by Bjorn Sjodin. This article utilizes the method and equations as presented in that blog post, and the main equation is rewritten here and slightly modified for the desired output, where M is the resultant multiplier for the material properties; A is the magnitude of the spatial variation field; N is the spatial frequency resolution; g is a randomly sampled Gaussian distribution with a mean of zero and a standard deviation of one; β is the spectral (smoothing) exponent; D is the spatial frequency magnitude; and Φ is the phase angle, which is randomly sampled from a uniform distribution that ranges from zero to pi:
The parameters utilized for the above spatial variation equation are shown in the following table:
| Parameter | Description | Value |
|---|---|---|
| N | Spatial frequency resolution | 20 |
| D | Spatial frequency magnitude | 0.4 |
| β | Spectral (smoothing) exponent | 0.8 |
| A | Magnitude of the spatial variation field | 0.005 |
Table 2. Parameters utilized for the spatial variation equation as presented in the previous blog post.
All elastic properties except for the Poisson’s ratio are multiplied by the multiplier M. The resulting spatial field for the CD elastic modulus, for one set of random seeds, is shown below.
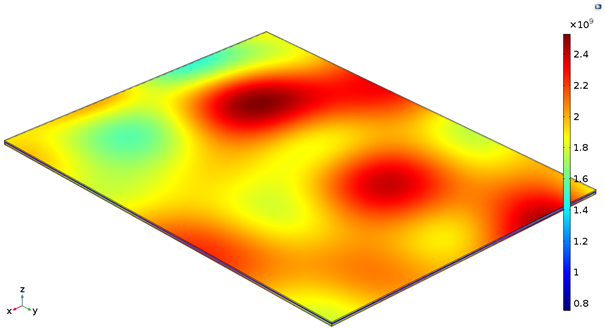
Spatial variation of the CD elastic modulus (in Pa), which represents the elastic modulus variation due to formation differences.
Since the inclusion of material variation can cause mesh dependency in a model, a parameter sweep was utilized to determine the mesh sensitivity of the model. The results of the mesh sensitivity study are shown in Figure 4. Since the percent error is very low (0.01 %) at a mesh max edge length of 1.0 mm, that mesh size is utilized through the rest of the study.
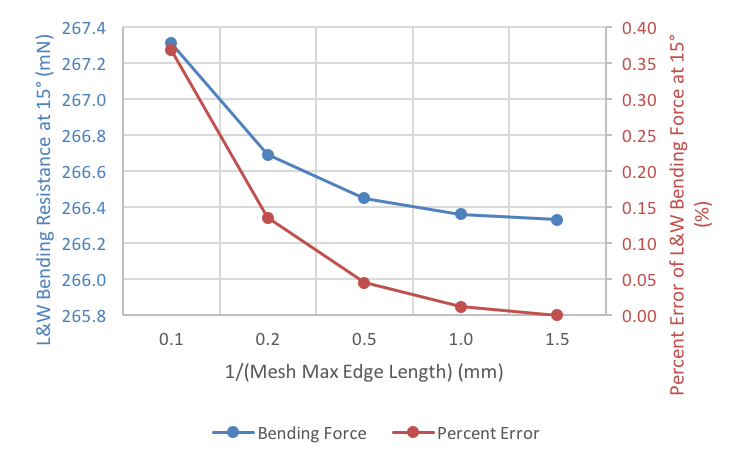
Mesh sensitivity of the model.
Additionally, random models can be sensitive to their own inherent randomness, so one must also determine the amount of repeat solutions (with different seeds for the randomly calculated values) that are required to draw a conclusion. The following figure shows how the average bending stiffness value converges with additional repeat solutions and how the confidence intervals bars decrease in size with an increased number of repeat solutions. The figure below shows that at least three repeat solutions should be utilized to get any confidence regarding the average L&W bending force at 15°. Therefore, this study will utilize four repeat solutions to ensure confidence in the conclusions. For even better confidence, more repeat solutions could be utilized.
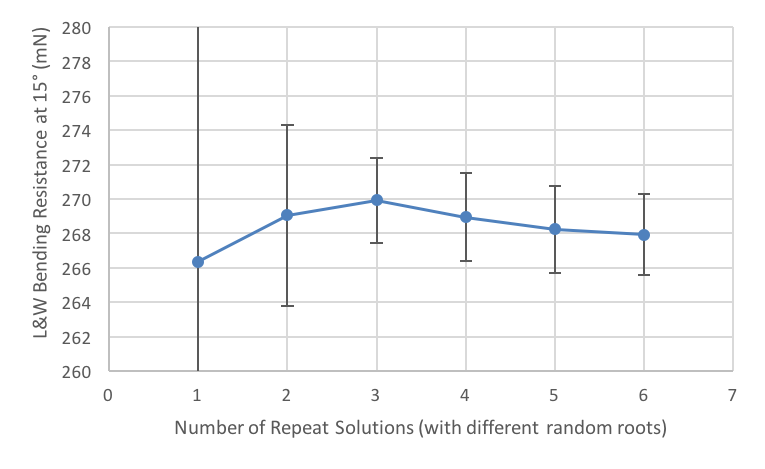
Randomness sensitivity of the model with confidence interval bars.
Material and parameter sweeps were utilized independently in order to automatically calculate the effects of the magnitude of density differences (i.e., the magnitude of the spatial variation field), as well as the effects of the floc size on the L&W bending resistance at 15°.
Discussing the Simulation Results
The resulting stress and strain fields during deformation are asymmetric, because the material properties themselves are asymmetric. As you can see below, the compressive CD strain field, on the surface of the bottom ply at the maximum deformation, is asymmetric.
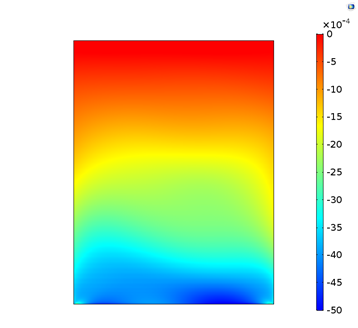
Compressive CD strain on the surface of the bottom ply for one of the repeat solutions. Note the asymmetric strain pattern, which is caused by the material variation.
In order to study the effect of the magnitude of density differences in the top ply on bending resistance, material sweeps were conducted with varying levels of the spatial magnitude variation field parameter (A). The results of these sweeps, which were repeated four times with different random seeds to ensure confidence in the results, are averaged and shown below, along with the 95% confidence interval of each averaged point. The 15° bending resistance increases as the spatial variation field magnitude approaches zero (a value of zero denotes perfect formation). This result would indicate that an improvement from the worst formation simulated
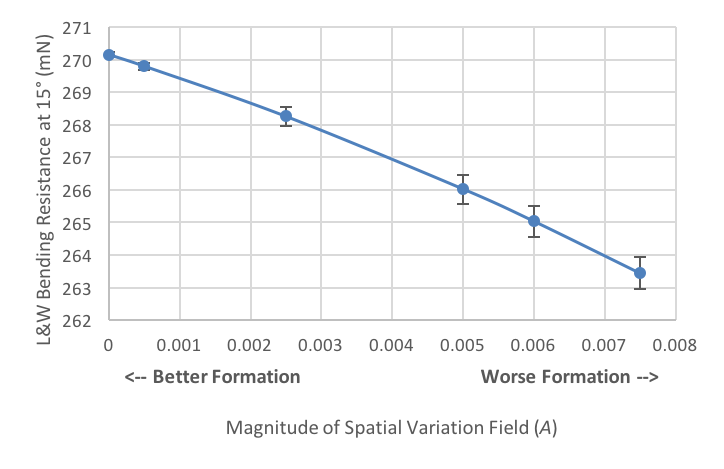
The effect of the magnitude of density differences on bending resistance.
To study the effect of the floc size, material sweeps were conducted with varying levels of the spatial frequency magnitude parameter (D) for the top ply. The results of these sweeps, which were repeated four times with different random seeds to provide sufficient confidence in the results, are averaged and shown below, along with the 95% confidence interval of each averaged point. The L&W bending resistance at 15° is greater on average for small flocs as compared to large flocs, which implies that large flocs are more detrimental to the bending resistance at 15° than small flocs. This result suggests that, if a papermaker reduces their floc size from the maximum to the minimum size considered in this article, the L&W bending resistance (15°) could be improved by 3.3–4.2%.
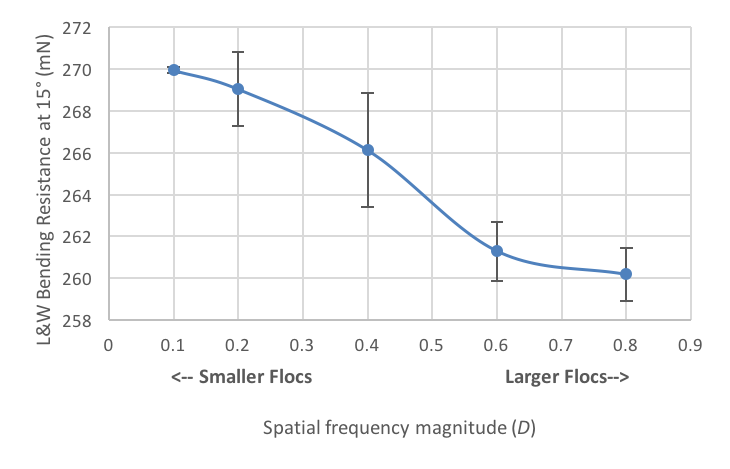
The effect of floc size on bending resistance.
With quantification of the possible improvements in L&W bending resistance at 15°, one can make cost–benefit analyses of potential capital investments. As an example, this could help one determine whether a new top-ply headbox would be worth the capital investment to improve bending resistance.
Editor’s note, 3/21/23: The corresponding model file has been added to the Application Exchange. You can find it here.
Lightness by Design, a COMSOL Certified Consultant, offers paper mechanics expertise along with simulation development and execution capabilities for advanced problems in paper mechanics.
Reference
- A. Hagman and M. Nygårds, “Thermographical Analysis of Paper During Tensile Testing and Comparison to Digital Image Correlation,” Experimental Mechanics, vol. 57, 325–339, 2017, doi:10.1007/s11340-016-0240-4
About the Guest Author
Eric is a consultant at Lightness by Design, a COMSOL Certified Consultant where he has a particular interest in paper-based packaging and aerospace structures. While these may seem like a random duo, the common links between these two applications are the utilization of lightweight load-bearing structures as well as fiber-based materials. Eric’s background in aerospace structural engineering includes both project experience as a consultant and formal BS education at Embry-Riddle Aeronautical University. After initial education in aerospace, Eric entered the exciting world of paper by pursuing a PhD in solid mechanics with a focus on paper mechanics at the KTH Royal Institute of Technology in Stockholm, Sweden, followed by 1.5 years in the R&D of the paper company WestRock. He has since been a consultant at Lightness by Design, where, in addition to consulting, he continues to develop FEM simulation tools (comprehensive user-defined materials and a virtual lab) that allow for advanced simulation of paper products and processes.




Comments (0)