Quadrupole mass filters, the key component of quadrupole mass spectrometers, filter ions by their charge-to-mass ratio, only allowing ions with a certain ratio to pass through the device. As such, a high transmission probability for a specific ion through the filter is desirable. However, fringe fields in the mass filter can affect this probability. By using multiphysics simulation, we can take a closer look at quadrupole mass filters and investigate the effect of fringe fields on these devices.
A Short Introduction to Mass Spectrometry
Mass spectrometry is a process that analyzes and sorts ions based on their charge-to-mass ratio. Typical mass spectrometers work by ionizing individual molecules or atoms, then moving and manipulating these ions with an external electric field.
A mass spectrometer’s inherent sensitivity yields itself to many applications, including identifying unknown biological compounds, determining chemical mixture compositions, detecting toxins in food sources, and space exploration. Today, these devices continue to improve, with new mass spectrometry machines able to analyze up to 30 components simultaneously, both in gas and liquid phases.
One type of mass spectrometer, a quadrupole mass spectrometer, allows only ions of a specific charge-to-mass ratio to pass through the device for each given ratio of voltages. This is accomplished with a quadrupole mass filter, a component of the spectrometer that consists of four cylindrical metal rods.

A quadrupole mass filter. Image by Fulvio314 — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
Today, we will use the Particle Tracing and AC/DC modules in COMSOL Multiphysics to simulate a mass filter and evaluate its performance in a quadrupole mass spectrometer.
Using Multiphysics Modeling to Evaluate a Quadrupole Mass Spectrometer Component
In order for a quadrupole mass spectrometer to successfully analyze a mixture, its mass filter needs to maintain a high transmission probability for a specific ion. This means that the filter must ensure that ions of only a certain charge-to-mass ratio are transmitted through the device.
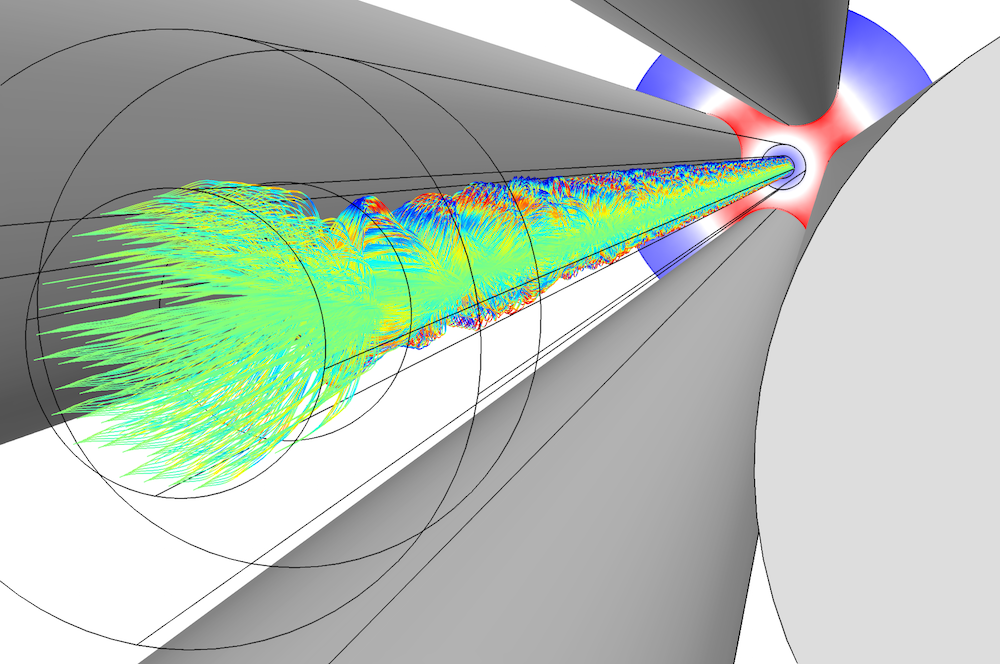
We can evaluate this ability by modeling a quadrupole mass filter and accounting for the effects of fringe fields located at its entrance and exit. These are important elements to include because fringe fields influence the transmission probability of a specific ion through a mass filter.

Simulations showing particle trajectories in a quadrupole mass spectrometer’s mass filter.
We can model the mass filter in two stages:
- Compute the DC and AC fields
- Calculate the ion trajectories, the motion of which is controlled by these same fields
Let’s start by taking a closer look at the design of our model. First, we use Poisson’s equation to calculate the electric potential, U, for the DC field. Next, we use the conservation of electric currents to compute the AC potential, V, for the AC field. For both of these cases, we apply a positive potential of magnitude on the north and south rods and a negative potential on the east and west rods. Further, to help accelerate the ions into the mass filter, we can apply small DC and AC biases to the ion aperture.
We also use the superposition of the AC and DC fields to build the total electric field that the particles experience when entering the modeling domain. It’s important to note that, because the equations solved for the AC and DC fields are linear, this is a valid assumption. A stationary electric field and one that changes over time both contribute to the total electric field.
Particle Tracing in a Quadrupole Mass Filter
For the next stage of the simulation, we calculate the trajectories of the ions that move through the filter. Ion motion is governed by Newton’s second law. The ions in this tutorial are released both at the simulation start time and at uniformly spaced times during the AC field’s first RF cycle. Over the course of the simulation, particles are released eleven different times between 0 seconds and 0.25 μs. Since the frequency of the AC field is 4 MHz, this ends up being one full RF cycle.
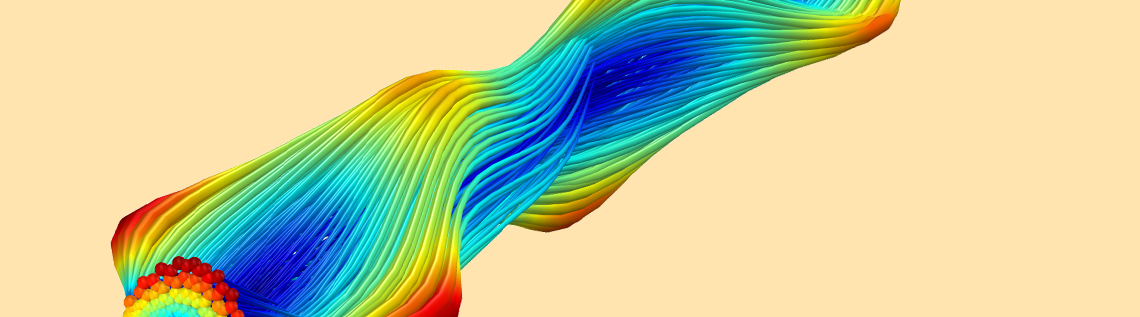
By accurately computing the ion trajectories, including the effects of the fringe fields, we are able to find the ion transmission. In this case, the plot shows that the ion transmission is very high, reaching 100%. This occurs because we choose a very stable operating point on the a-q curve. Here, a and q refer to coefficients in the Mathieu equation, which can be used to compute an approximate solution of ion motion in a quadrupole mass filter. In our study, the ions remain in the quadrupole mass filter for about 140 RF cycles.
Particle trajectories in a quadrupole mass filter. The z-component of the total force is indicated by the color.
Taking a Look at the Design Elements of the Mass Filter
We can use these simulation results to see the effects of different design elements on the quadrupole mass filter. For instance, in our model, we include a biased plate surrounding the ion aperture. This causes the ions to gain energy as they move through the filter. As we can see in the plot below, the mean energy of these ions is 5 eV over a range of about 3 eV. Such a spread in energy may be due to the small DC and AC bias. Since the AC bias can be either positive or negative, the ions may accelerate or decelerate based on which RF cycle phase they are released in.
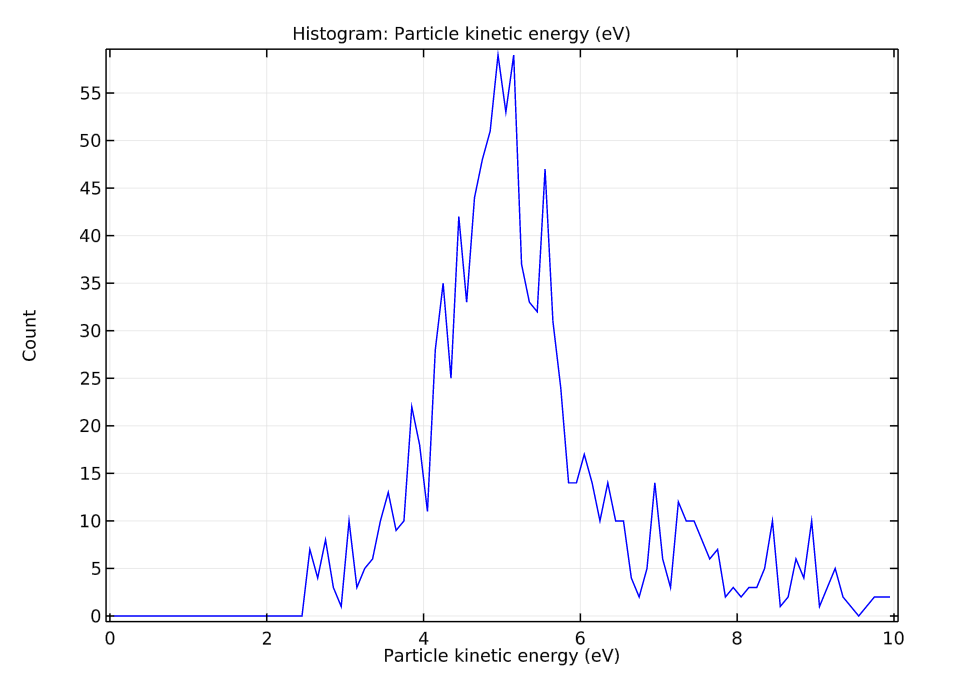
The ions’ particle kinetic energy distribution when they reach the collector.
In this blog post, we used multiphysics modeling to accurately analyze a mass filter for use in a quadrupole mass spectrometer. Optimizing quadrupole mass filter designs can aid in the development of even more accurate mass spectrometers in the future.
Learn More About Simulating Spectrometers in COMSOL Multiphysics
- Download the tutorial model: Quadrupole Mass Spectrometer
- Check out these other spectrometer tutorials:
- Read about ray tracing in monochromators and spectrometers on the blog
- Learn about diffraction gratings, which are often found in monochromators and spectrometers





Comments (0)