
Standards form an integral part of the work we do as engineers, providing a common language for communicating complex information. But standards committees are not omnipotent and sometimes revised standards are not universally adopted. This has happened in the case of the standards for piezoelectric materials, particularly for quartz. This blog post explains the multiple standards used to describe piezoelectrics in literature. Although the particular focus of this post is on quartz, the standards described apply for any piezoelectric material.
Piezoelectric Materials
Piezoelectric materials become electrically polarized when strained. From a microscopic perspective, the displacement of charged atoms within the crystal unit cell (when the solid is deformed) produces a net electric dipole moment within the medium. In certain crystal structures, this combines to give an average macroscopic dipole moment and a corresponding net electric polarization. This effect, known as the direct piezoelectric effect, is always accompanied by the inverse piezoelectric effect, in which the solid becomes strained when placed in an electric field.
Several material properties must be defined in order to fully characterize the piezoelectric effect within a given material. The relationship between the material polarization and its deformation can be defined in two ways: the strain-charge or the stress-charge form. Different sets of material properties are required for each of these equation forms.
To complicate things further, there are two standards used in the literature: the IEEE 1978 Standard and the IRE 1949 standard, and the material properties take different forms within the two standards. IEEE actually revised the 1978 standard in 1987, but this version of the standard contained a number of errors and was subsequently withdrawn. Confused yet? I was when I first started reading the literature!
Today’s blog post describes in detail the different equation forms and standards, with a focus on the particular case of quartz — the material that causes the most confusion. In both academia and industry, the quartz material properties are commonly defined within the older 1949 IRE standard. Meanwhile, other materials are now almost always defined using the 1978 IEEE standard. To make matters worse, it is not common to indicate which standard is being employed when specifying the material properties.
Two Equation Forms: The Strain-Charge and the Stress-Charge Form
The coupling between the structural and electrical domains can be expressed in the form of a connection between the material stress and its permittivity at constant stress or as a coupling between the material strain and its permittivity at constant strain. The two forms are given below.
Strain-Charge Form
The strain-charge form is written as:
\bf{S}=s_E \bf{T}+d^T \bf{E} \\[3mm]
\bf{D}=d \bf{T}+\epsilon_0 \epsilon_{rT} \bf{E}
\end{array}
where S is the strain, T is the stress, E is the electric field, and D is the electric displacement field. The material parameters sE, d, and εrT correspond to the material compliance, coupling properties, and relative permittivity at constant stress. ε0 is the permittivity of free space. These quantities are tensors of rank 4, 3, and 2, respectively. The tensors, however, are highly symmetric for physical reasons. They can be represented as matrices within an abbreviated subscript notation, which is usually more convenient. In literature, the Voigt notation is almost always used.
Within this notation, the above two equations can be written as:
\left(
\begin{array}{l}
S_{xx} \\
S_{yy} \\
S_{zz} \\
S_{yz} \\
S_{xz} \\
S_{xy} \\
\end{array}
\right)
=
\left(
\begin{array}{llllll}s_{E11} & s_{E12} &s_{E13} &s_{E14} &s_{E15} &s_{E16}\\
s_{E21} & s_{E22} &s_{E23} &s_{E24} &s_{E25} &s_{E26}\\
s_{E31} & s_{E32} &s_{E33} &s_{E34} &s_{E35} &s_{E36}\\
s_{E41} & s_{E42} &s_{E43} &s_{E44} &s_{E45} &s_{E46}\\s_{E51} & s_{E52} &s_{E53} &s_{E54} &s_{E55} &s_{E56}\\s_{E61} & s_{E62} &s_{E63} &s_{E64} &s_{E65} &s_{E66}\\\end{array}
\right)\left(
\begin{array}{l}T_{xx} \\
T_{yy} \\
T_{zz} \\
T_{yz} \\
T_{xz} \\
T_{xy} \\
\end{array}
\right)
+
\left(
\begin{array}{lll}
d_{11} & d_{21} & d_{31} \\
d_{12} & d_{22} & d_{32} \\
d_{13} & d_{23} & d_{33} \\
d_{14} & d_{24} & d_{34} \\
d_{15} & d_{25} & d_{35} \\
d_{16} & d_{26} & d_{36} \\
\end{array}
\right)
\left(
\begin{array}{l}
E_{x} \\
E_{y} \\
E_{z} \\
\end{array}
\right)
\\
\left(
\begin{array}{l}
D_{x} \\
D_{y} \\
D_{z} \\
\end{array}
\right)
=
\left(
\begin{array}{llllll}
d_{11} & d_{12} &d_{13} & d_{14} & d_{15} & d_{16}\\
d_{21} & d_{22} &d_{23} & d_{24} & d_{25} & d_{26}\\
d_{31} & d_{32} &d_{33} & d_{34} & d_{35} & d_{36}\\
\end{array}
\right)\left(
\begin{array}{l}
T_{xx} \\
T_{yy} \\
T_{zz} \\
T_{yz} \\
T_{xz} \\
T_{xy} \\
\end{array}
\right)
+
\epsilon_0 \left(
\begin{array}{lll}
\epsilon_{rT11} & \epsilon_{rT12} & \epsilon_{rT13} \\
\epsilon_{rT21} & \epsilon_{rT22} & \epsilon_{rT23} \\
\epsilon_{rT31} & \epsilon_{rT32} & \epsilon_{rT33} \\
\end{array}
\right)
\left(
\begin{array}{l}
E_{x} \\
E_{y} \\
E_{z} \\
\end{array}
\right)
\\
\end{array}
Stress-Charge Form
The stress-charge form is as follows:
\bf{T}=c_E \bf{S}-e^T \bf{E} \\[3mm]
\bf{D}=e \bf{S}+\epsilon_0 \epsilon_{rS} \bf{E}
\end{array}
The material parameters cE, e, and εrS correspond to the material stiffness, coupling properties, and relative permittivity at constant strain. ε0 is the permittivity of free space. Once again, these quantities are tensors of rank 4, 3, and 2 respectively, but can be represented using the abbreviated subscript notation.
Using the Voigt notation and writing out the components gives:
\left(
\begin{array}{l}
T_{xx} \\
T_{yy} \\
T_{zz} \\
T_{yz} \\
T_{xz} \\
T_{xy} \\
\end{array}
\right)
=
\left(
\begin{array}{llllll}c_{E11} & c_{E12} &c_{E13} &c_{E14} &c_{E15} &c_{E16}\\
c_{E21} & c_{E22} &c_{E23} &c_{E24} &c_{E25} &c_{E26}\\
c_{E31} & c_{E32} &c_{E33} &c_{E34} &c_{E35} &c_{E36}\\
c_{E41} & c_{E42} &c_{E43} &c_{E44} &c_{E45} &c_{E46}\\c_{E51} & c_{E52} &c_{E53} &c_{E54} &c_{E55} &c_{E56}\\c_{E61} & c_{E62} &c_{E63} &c_{E64} &c_{E65} &c_{E66}\\\end{array}
\right)\left(
\begin{array}{l}S_{xx} \\
S_{yy} \\
S_{zz} \\
S_{yz} \\
S_{xz} \\
S_{xy} \\
\end{array}
\right)
+
\left(
\begin{array}{lll}
e_{11} & e_{21} & e_{31} \\
e_{12} & e_{22} & e_{32} \\
e_{13} & e_{23} & e_{33} \\
e_{14} & e_{24} & e_{34} \\
e_{15} & e_{25} & e_{35} \\
e_{16} & e_{26} & e_{36} \\
\end{array}
\right)
\left(
\begin{array}{l}
E_{x} \\
E_{y} \\
E_{z} \\
\end{array}
\right)
\\
\left(
\begin{array}{l}
D_{x} \\
D_{y} \\
D_{z} \\
\end{array}
\right)
=
\left(
\begin{array}{llllll}
e_{11} & e_{12} &e_{13} & e_{14} & e_{15} & e_{16}\\
e_{21} & e_{22} &e_{23} & e_{24} & e_{25} & e_{26}\\
e_{31} & e_{32} &e_{33} & e_{34} & e_{35} & e_{36}\\
\end{array}
\right)\left(
\begin{array}{l}
S_{xx} \\
S_{yy} \\
S_{zz} \\
S_{yz} \\
S_{xz} \\
S_{xy} \\
\end{array}
\right)
+
\epsilon_0 \left(
\begin{array}{lll}
\epsilon_{rS11} & \epsilon_{rS12} & \epsilon_{rS13} \\
\epsilon_{rS21} & \epsilon_{rS22} & \epsilon_{rS23} \\
\epsilon_{rS31} & \epsilon_{rS32} & \epsilon_{rS33} \\
\end{array}
\right)
\left(
\begin{array}{l}
E_{x} \\
E_{y} \\
E_{z} \\
\end{array}
\right)
\\
\end{array}
The matrices defined in the above equations are the key material properties that need to be defined for a piezoelectric material. Note that for many materials, a number of the elements in each of the matrices are zero and several others are related, as a result of the crystal symmetry.
Using the international notation for describing crystal symmetry, the symmetry group of quartz is Trigonal 32. The nonzero matrix elements take different values within different standards, which can result in confusion when specifying the material properties for a simulation, especially for quartz, where two different standards are commonly employed.
Finally, there is another complication in the case of quartz. Quartz crystals do not have symmetry planes parallel to the vertical axis. Correspondingly, they occur in two types: left- or right-handed (this is known as enantiomorphism). Each one of these enantiomorphic forms results in different signs for particular elements in the material property matrices.
The material property matrices appropriate for quartz and other Trigonal 32 materials are shown below. Note that the symmetry relationships between elements in the matrix hold irrespective of the standard used or whether the material is right- or left-handed.
\left(
\begin{array}{cccccc}
c_{E11} & c_{E12} &c_{E13} & c_{E14} & 0 & 0\\
c_{E12} & c_{E11} &c_{E13} & -c_{E14} &0 & 0\\
c_{E13} & c_{E13} &c_{E33} & 0 & 0 & 0\\
c_{E14} & -c_{E14} & 0 & c_{E44} & 0 & 0 \\
0 & 0 & 0 & 0 & c_{E44} & c_{E14}\\
0 & 0 & 0 & 0 & c_{E14} & \frac{1}{2}\left(c_{E11}-c_{E12}\right)\\
\end{array}
\right)
&
\left(
\begin{array}{cccccc}
s_{E11} & s_{E12} &s_{E13} & s_{E14} & 0 & 0\\
s_{E12} & s_{E11} &s_{E13} & -s_{E14} &0 & 0\\
s_{E13} & s_{E13} &s_{E33} & 0 & 0 & 0\\
s_{E14} & -s_{E14} & 0 & s_{E44} & 0 & 0 \\
0 & 0 & 0 & 0 & s_{E44} & 2 s_{E14}\\
0 & 0 & 0 & 0 & 2 s_{E14} & 2\left(s_{E11}-s_{E12}\right)\\
\end{array}
\right)
\\
\left(
\begin{array}{cccccc}
e_{11} &-e_{11} & 0 & e_{14} & 0 & 0 \\
0 & 0 & 0 & 0 & -e_{14} & -e_{11}\\
0 & 0 & 0 & 0 & 0 & 0 \\
\end{array}
\right)
&
\left(
\begin{array}{cccccc}
d_{11} & -d_{11} & 0 & d_{14} & 0 & 0 \\
0 & 0 & 0 & 0 & -d_{14} & -2d_{11} \\
0 & 0 & 0 & 0 & 0 & 0\\
\end{array}
\right)
\\
\left(
\begin{array}{ccc}
\epsilon_{rS11} & 0 & 0 \\
0 & \epsilon_{rS11} & 0 \\
0 & 0 & \epsilon_{rS33} \\
\end{array}
\right)
&
\left(
\begin{array}{ccc}
\epsilon_{rT11} & 0 & 0 \\
0 & \epsilon_{rT11} & 0 \\
0 & 0 & \epsilon_{rT33} \\
\end{array}
\right)
\\
\end{array}
Two Standards: 1949 IRE and 1978 IEEE
Having defined a set of material properties in terms of matrices that operate on the different components of the stress or the strain in the x,y,z axes system, all that remains is to define a consistent set of axes to use when writing down the material properties.
Correspondingly, all of the standards define a consistent set of axes for each of the relevant crystal classes. Unfortunately, in the particular case of quartz, subsequent standards have not used the same sets of axes, and the adoption of the most recent standard has not been widespread. Therefore, it is important to understand exactly which standard a given set of material properties is defined in.
The two relevant standards are:
- The IEEE 1978 standard:
- This is usually employed for materials other than quartz in most of the literature. Sometimes, it is used to specify the quartz material properties, for example, B. A. Auld’s book Acoustic Fields and Waves in Solids employs this standard.
- The IRE 1949 standard:
- This is usually used for the material properties of quartz in literature.
The orientation of the axes set with the crystal can be determined by specifying the orientation with respect to the atoms in the unit cell of the crystal (which is not that helpful in practice) or by specifying the orientation with respect to the crystal forms. A crystal form is a set of crystal faces or planes that are related by symmetry. Particular forms commonly appear in crystal specimens found in rocks and are used to identify different minerals.
The Quartz Page has a series of helpful figures for identifying the common crystal forms, termed m, r, s, x, and z, as well as a further page specifying the Miller indices of the corresponding planes. Since the standards typically use crystal forms to orientate the axes, this approach is adopted in the figure below, which shows the two axes sets that relate to the 1978 and 1949 standards. Note that both left- and right-handed quartz are shown in the figure.
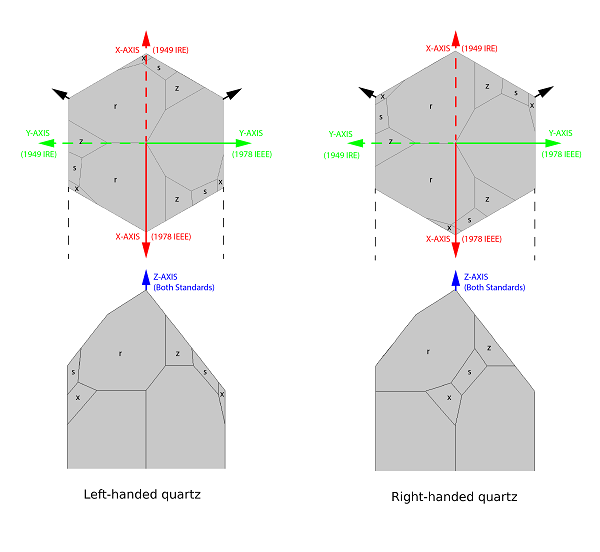
Crystallographic axes defined for quartz within the 1978 IEEE standard (solid lines) and the 1949 standard (dashed lines). Click on the image to view a larger version.
As a result of the different crystal axes, the signs of the material properties for both right- and left-handed quartz can change depending on the particular standard employed. The table below summarizes the different signs that occur for the quartz material properties:
|
IRE 1949 Standard |
IEEE 1978 Standard |
|||
|---|---|---|---|---|
|
Material Property |
Right-Handed Quartz |
Left-Handed Quartz |
Right-Handed Quartz |
Left-Handed Quartz |
| sE14 |
+ |
+ |
— |
— |
| cE14 |
— |
— |
+ |
+ |
| d11 |
— |
+ |
+ |
— |
| d14 |
— |
+ |
— |
+ |
| e11 |
— |
+ |
+ |
— |
| e14 |
+ |
— |
+ |
— |
Two Definitions for the Crystal Cut
Usually, piezoelectrics, such as quartz, are supplied in thin wafers that have been cut at a particular angle, with respect to the crystallographic axes. The orientation of a piezoelectric crystal cut is frequently defined by the system used in both the 1949 and 1978 standards. The orientation of the cut, with respect to the crystal axes, is specified by a series of rotations, using notation that takes the form illustrated below:
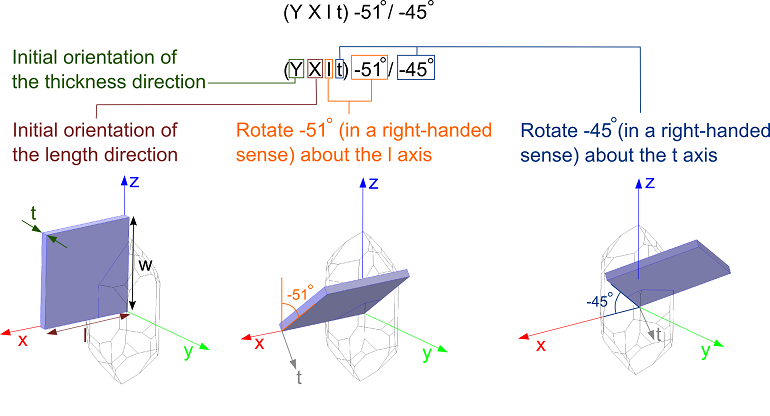
Diagram showing how a GT cut plate of quartz is defined in the IEEE 1978 standard. The crystal shown is right-handed quartz.
The first two letters of the notation given in the brackets describe the orientation of the thickness and length of the plate that is being cut from the crystal. From the figure on the left, it is clear that the thickness direction (t) is aligned with the Y-axis and the length direction (l) is aligned with the X-axis. The plate also has a third dimension, its width (w). After the first two letters, a series of rotations are defined about the edges of the plate.
In the example above, the first rotation is about the l-axis, with an angle of -51°. The negative angle means that the rotation takes place in the opposite direction to a right-handed rotation about the axis. Finally, an additional rotation about the resulting t-axis is defined, with an angle (in a right-handed sense) of -45°.
Most practical cuts use one or two rotations, but it is possible to have up to three rotations within the standard, allowing for completely arbitrary plate orientations.
Note that since the crystallographic axes are defined differently in the 1949 and the 1978 standards, the crystal cut definitions differ between the two. A common cut for quartz plates is the AT cut, which is defined in the two standards in the following manner:
| Standard |
AT Cut Definition |
|---|---|
| 1949 IRE |
(YXl) 35.25° |
| 1978 IEEE |
(YXl) -35.25° |
The figure below shows how the two alternative definitions of the AT cut correspond to the two alternative definitions of the axes employed in the standards.
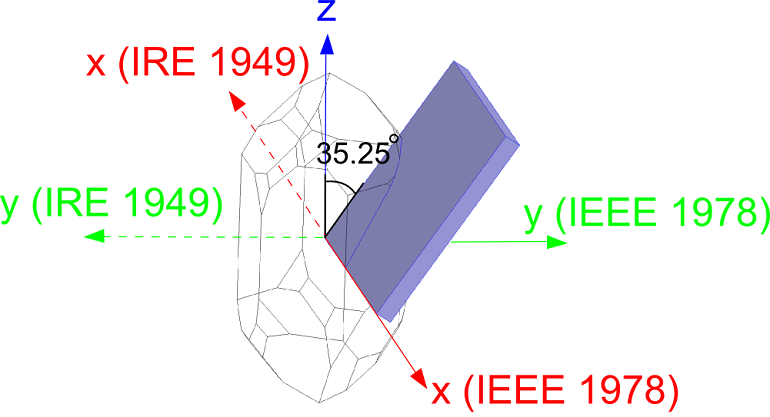
The AT cut of quartz is defined as (YXl) 35.25° in the IRE 1949 standard and (YXl) -35.25° in the IEEE 1978 standard. The figure shows the cut defined in a right-handed crystal of quartz. The reason for the difference between the standards is related to the different conventions for the orientation of the crystallographic axes. In the IRE 1949 standard, the rotation occurs in a positive or right-handed sense about the l-axis (which in this case is aligned with the X-axis). As a result of the different axes set employed in the IEEE 1978 standard, the rotation corresponds to a negative angle in this standard.
Next Steps
We have now seen how the two different standards result in different definitions of the material properties and different definitions of the crystal cuts.
In a follow-up blog post, we will explore how to set up a COMSOL Multiphysics model using the two standards. COMSOL Multiphysics provides material properties for quartz using both of the available standards, so it is possible to set up a model using whichever standard you are most familiar with. Stay tuned for that.
Editor’s note: We published a follow-up blog post on this topic on 1/27/16. Read about applying the standards in your COMSOL Multiphysics models here.




Comments (1)
James Ransley
February 3, 2016Please note that some further subtleties related to the application of the two standards are discussed in the related blog post on applying the standards:
http://www.comsol.com/blogs/piezoelectric-materials-applying-the-standards/