
When a superconducting magnet suddenly transitions to a normal state — known as a quench — its coils may overheat. Quench detection and protection systems are often included in the magnets to enable safer operation. For these systems to be effective, it’s important to understand the resulting electrothermal transient phenomena that take place within the magnet. Using numerical simulation, we can develop sophisticated systems that prevent possible disruption effects.
The Large Hadron Collider: The Most Powerful Particle Accelerator
Built by the European Organization for Nuclear Research (CERN), the Large Hadron Collider (LHC) is a structure that holds many records. It’s not only the most complex experimental facility that has ever been built and the largest single machine that exists, but it’s also currently the world’s largest and most powerful particle accelerator. The LHC has the potential to provide answers to various physics-related questions. (Take a virtual tour to see it for yourself.)

Part of the Large Hadron Collider’s tunnel. Image by Julian Herzog — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
Behind the operation of the accelerator is a 27-kilometer ring of superconducting magnets and multiple accelerating structures that give particles an energy boost. These magnets, which are made of coils that can operate in the superconducting state, maintain a strong magnetic field that guides particle beams around the accelerator ring.
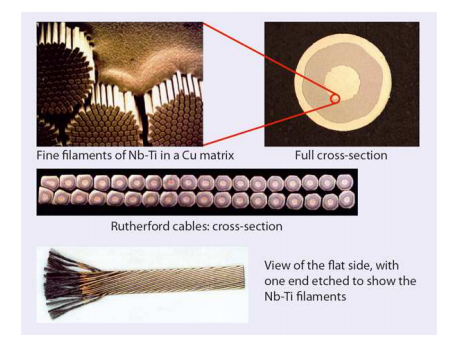
To create such strong fields, iron-yoked electromagnets, fully wound with rectangular cables, are used. Nb-Ti filaments are embedded inside a copper matrix to form a strand, which is then twisted and wrapped in a polyamide insulation layer. When the cable is cooled to 1.9 K, the filaments are able to reach the superconducting state, which in turn allows the cable to carry greater current densities.
Left: Cross section of the magnet. Right: Cable layout. Images by L. Bortot, M. Maciejewski, M. Prioli, A.M. Fernandez Navarro, S. Schöps, I. Cortes Garcia, B. Auchmann, and A.P. Verweij and taken from their COMSOL Conference 2016 Munich paper.
When designing superconducting magnets like those in the LHC, it’s important to consider potential scenarios that could cause disruptive effects. One such example is quenches.
Studying Quenches in Superconducting Magnets
A quench refers to the sudden transition of a magnet from the superconducting state to a normal state. This process occurs when the working point of a superconductor magnet moves out of what is called the critical space, which then causes energy stored in the magnetic field to be released as Ohmic losses.
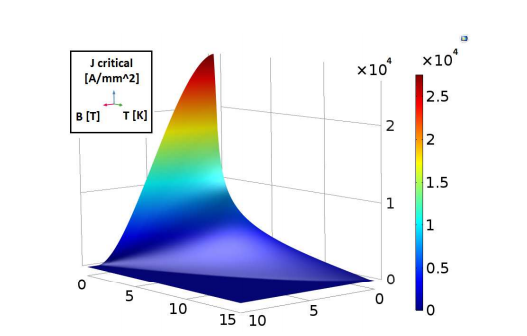
Plot of the critical surface for the filaments, with the maximum current density shown as a function of the magnetic and temperature fields. Image by L. Bortot, M. Maciejewski, M. Prioli, A.M. Fernandez Navarro, S. Schöps, I. Cortes Garcia, B. Auchmann, and A.P. Verweij and taken from their COMSOL Conference 2016 Munich paper.
When a quench takes place, it forces the conduction current to travel from the filaments to the copper matrix in which they are embedded. Such movement can cause the coils inside the magnet to overheat. In an effort to prevent possible disruption effects, magnet designs typically include quench detection and protection systems. Ensuring the effectiveness of these systems, however, requires an understanding of the electrothermal transient phenomena that takes place within the magnet.
Recognizing this, a team of researchers from CERN simulated a quench event in a superconducting magnet, using a main dipole from the LHC as their point of analysis. Let’s see how the flexibility and functionality of the COMSOL Multiphysics® software helped them to simulate this complex design.
Building an Electrothermal Model of a Superconducting Magnet
When modeling a superconducting magnet, one of the challenges is accounting for the number of half turns. For the main dipole of the LHC, this number is 320. Each of these half turns must be set up with its respective variables and operators in order to compute relevant quantities. This process is not only time consuming, but it is also prone to error.
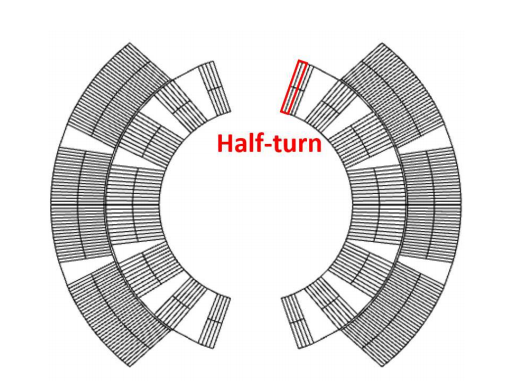
Cross section of a magnet’s coil with highlighted half turns. Image by L. Bortot, M. Maciejewski, M. Prioli, A.M. Fernandez Navarro, S. Schöps, I. Cortes Garcia, B. Auchmann, and A.P. Verweij and taken from their COMSOL Conference 2016 Munich paper.
To speed up the model creation process and reduce the chances of error, the researchers from CERN developed an automated Java® workflow that relies on the COMSOL API. The structure of this application is based on three main functional layers:
- Top layer, which enables users to describe a desired model with text input files
- Middle layer, which includes numerical methods needed to formulate input parameters for the API
- Bottom layer, which offers classes to embed functionalities from the COMSOL API for use with Java®
With this workflow in place, the magnet’s half turns were implemented in the model design with the indexing feature. This feature is quite useful as it allows you to redefine variables that have a formulation that’s common to every turn. Therefore, only a single variable is needed to describe a group of domains that share the same property.
Further, through the Java® workflow, the team at CERN was able to define various geometrical primitives, from points to lines, to construct their 2D model. Including model symmetries in the application helped to simplify the modeling process.
To minimize the number of mesh nodes, and thus the computational time, a combination of unstructured and structured elements was included in the model’s mesh. In order to ensure the accuracy of the results, the researchers performed a mesh sensitivity analysis.
The physics implemented in the model accounted for nonlinear temperature and field-dependent material properties and eddy currents induced within the superconducting cable. The latter enabled the team to calculate the quench initiation and propagation.
Simulation Results for Two Time-Dependent Studies
The analysis includes two time-dependent studies that were performed consecutively:
- The magnet’s current, linearly ramped up to the nominal value
- The exponential current decay, simulated at a time constant of 0.1 s
Note that the second study uses the final state of the first study as its initial condition.
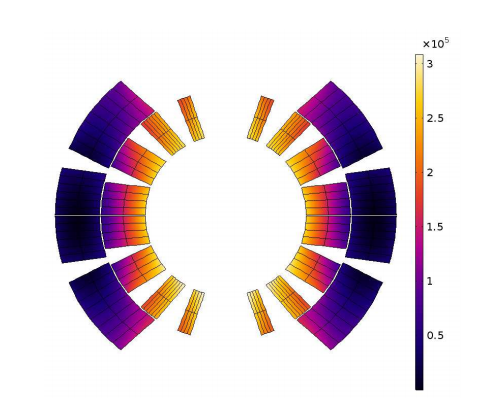
The researchers first looked at the behavior of the magnet during fast discharge. The plot on the left shows the magnetic field in the magnet at nominal conditions. During a linear ramp up of 100 A/s, the field’s variation produces eddy currents. The equivalent magnetization of these currents is shown in the plot on the right.
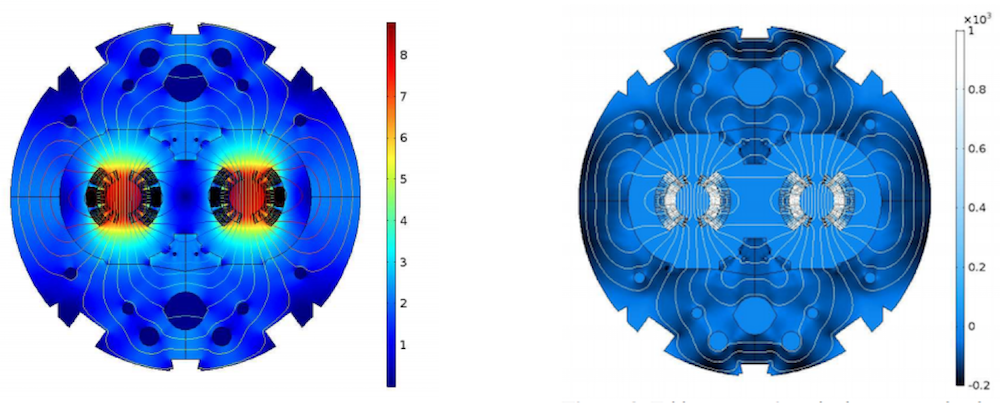
Left: Magnetic field in the magnet at nominal current. Right: Equivalent magnetization of eddy currents during linear ramp up of 100 A/s. Images by L. Bortot, M. Maciejewski, M. Prioli, A.M. Fernandez Navarro, S. Schöps, I. Cortes Garcia, B. Auchmann, and A.P. Verweij and taken from their COMSOL Conference 2016 Munich paper.
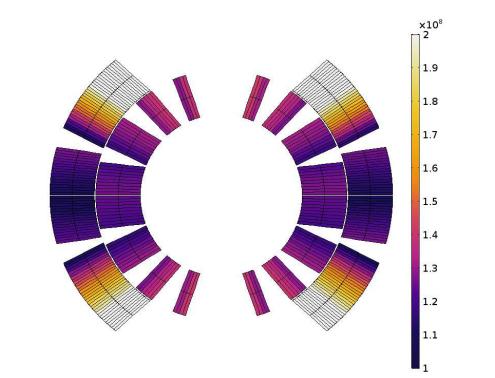
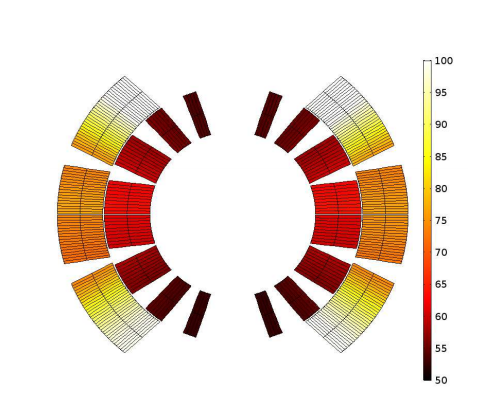
The losses that are generated impact the magnetic field, affecting the magnetic equivalent electrical impedance. They also deposit energy in the magnetic coil, dissipating some of the energy stored inside the magnetic field. If they are high enough, these losses can cause the temperature of the superconductor to rise beyond the critical surface. This can in turn cause the superconductor to transition to a normal state. At this stage, Ohmic losses are dominant in causing the magnet’s coil to heat up. The temperature of the coil is extracted after 0.5 s and visualized in a plot.
Left: Eddy current losses deposited in the coil. Center: Ohmic losses deposited in the coil. Right: Temperature distribution in the coil. Images by L. Bortot, M. Maciejewski, M. Prioli, A.M. Fernandez Navarro, S. Schöps, I. Cortes Garcia, B. Auchmann, and A.P. Verweij and taken from their COMSOL Conference 2016 Munich paper.
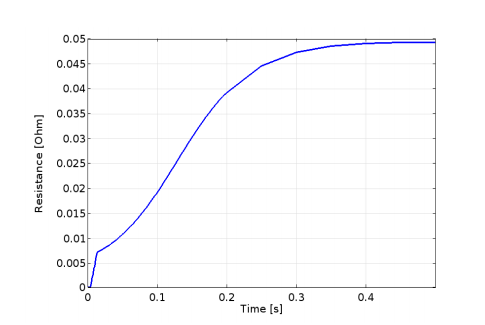
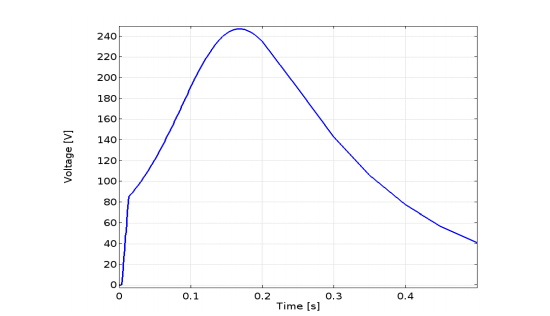
Along with the coil temperature, coil resistance and voltage are also extracted from the simulation results. These values can be used as input when designing protection systems for superconducting magnets.
The coil’s resistance (left) and resistive voltage (right) as a function of time. Images by L. Bortot, M. Maciejewski, M. Prioli, A.M. Fernandez Navarro, S. Schöps, I. Cortes Garcia, B. Auchmann, and A.P. Verweij and taken from their COMSOL Conference 2016 Munich paper.
To learn more about this simulation research, read the full COMSOL Conference paper: “Simulation of Electro-Thermal Transients in Superconducting Accelerator Magnets“. For more examples of using COMSOL Multiphysics to simulate superconductors, browse the resources listed below.
Additional Resources on Simulating Superconductors
- Learn about modeling superconductivity in a YBCO wire
- Explore the use of simulation in designing fully superconducting rotating machines
Oracle and Java are registered trademarks of Oracle and/or its affiliates.




Comments (0)