Blog Posts Tagged Technical Content

How to Use Job Sequences to Save Data After Solving Your Model
This how-to blog post is for those who want to automate common tasks after solving a model. Learn how to use job sequences here.

How to Export Images Automatically After Solving Your Model
Did you know that COMSOL Multiphysics® can automatically export results images and animations after your model solves? Get the details here.

How to Import Images and Loft a Solid
Say you want to model an irregular shape, like a human head. How do you set up the geometry? Here, we go over how to do just that by importing images and lofting a solid.

Methods That Accelerate the Modeling of Bandpass-Filter-Type Devices
Designing bandpass-filter type high-Q devices with the finite element method in the frequency domain? Here are some methods you can use to speed up the modeling process.
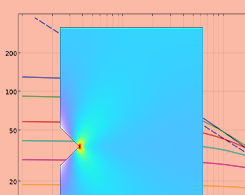
How Should I Evaluate Singular Stress Fields?
Explore the properties of singular stress fields and see some possible approaches for evaluating them in COMSOL Multiphysics®.
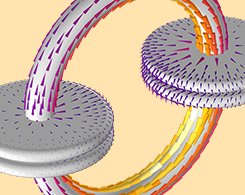
Learning from the Two-Capacitor Paradox: Do Capacitance and Inductance Exist?
What is the two-capacitor paradox? How can it be resolved with modeling and simulation? Do capacitance and inductance exist? Get answers here.

Introduction to the Composite Materials Module
Explore the Composite Materials Module, an add-on to COMSOL Multiphysics® that includes specialized functionality for modeling layered composite structures.
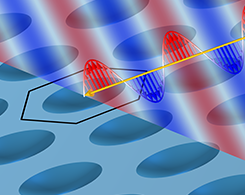
Understanding Higher-Order Diffraction
Explore how to use the Ewald sphere to study diffraction from planar periodic structures. (Interact directly with the model to get the full picture!)
