The COMSOL Multiphysics® software is well suited for modeling RF heating, where one needs to solve for both the electromagnetic fields and the temperature distribution over time. Although you might think that you need the RF Module for all types of problems involving RF heating, you can often use either the RF Module or the AC/DC Module, and you can use several different physics interfaces for some typical problems in this area. Let’s learn more!
Table of Contents
- Introduction
- Solving via the Electromagnetic Waves Physics Interface
- Solving via the Electric Currents Interface
- Solving via the Magnetic and Electric Fields Physics Interface
- Two Other Approaches
- Closing Remarks
Introduction
When starting an electromagnetic modeling problem, the question of which physics interface within COMSOL Multiphysics® to use can sometimes lead to a quite involved discussion. A high-level overview of this is given in our blog post “Computational Electromagnetics Modeling: Which Module to Use?”. However, sometimes there are areas of significant overlap in usability between different physics interfaces, so different modeling approaches can lead to the same result. This is good to know since different approaches have different benefits. For instance, some approaches have lower computational costs, but more expensive approaches can provide additional insight.
It’s important to emphasize that these areas of overlap can be quite case specific and should be carefully validated against each other. To demonstrate, we will address one case where several different approaches can be used. The situation we will model is shown below.
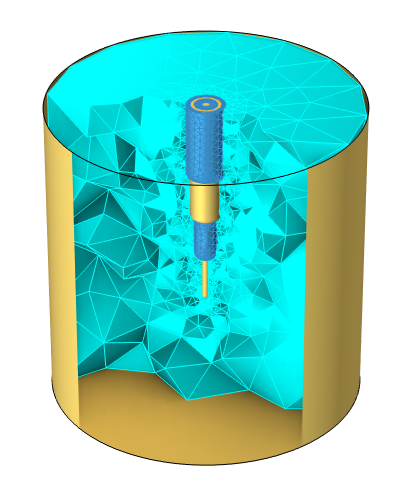
The system under consideration: a coaxial probe inserted into a metallic cavity filled with a sample of lossy dielectric material.
An RF source is connected via a coaxial cable (coax) to a simple probe inserted into a metallic cylindrical cavity (2 cm high and 2 cm in diameter) that is completely filled with a lossy material that we want to heat up. The probe is a continuation of the coax, with the insulation and conductors exposed and rounded off. The range of frequencies that will be considered is 100 kHz–1 GHz.
The material within the cavity is a lossy dielectric material, with a relative permittivity of 50 and a conductivity of 30 mS/m over the entire frequency range of interest. Although no materials have constant properties at all frequencies, it’s reasonable to assume nearly constant properties over some ranges. The metal of the cavity walls and coax has a conductivity of 6e7 S/m, about that of copper. The insulator within and around the coax has a relative permittivity of 1.75 and conductivity of 1e-12 S/m. The radius of the inner conductor is 0.25 mm, and the inside radius of the outer conductor is 0.75 mm, forming a low-loss coaxial transmission line of 50 Ω impedance.
Solving via the Electromagnetic Waves Physics Interface
We will start our modeling problem by considering just the highest frequency, 1 GHz. This will unambiguously require the Electromagnetic Wave, Frequency Domain physics interface of the RF Module since it’s near a cavity resonance. We can rigorously arrive at this conclusion by performing an eigenfrequency analysis of this lossy-dielectric filled cavity. The questions that we have to better consider are how low in frequency we can go with this interface and which boundary conditions we should use.
With respect to the boundary conditions, we know that the skin depth of the metal is very small over most of the frequency range. This justifies us starting with the Impedance boundary condition and not modeling the electromagnetic fields inside of the metal domains. We will eventually want to check this more carefully at the lowest frequency range, since at 100 kHz the skin depth is comparable to the thickness of the coax conductors. The outer conductor of the coax is electrically connected to the cavity walls via the Perfect Electric Conductor boundary condition, which represents an electrical connection without loss.
It’s tempting to think of the cavity wall and the outer conductor as being grounded, but, as we’ve discussed in our blog post “Voltage and Ground When Modeling Wave-Like EM Fields”, we should be quite careful and precise in our thinking and terminology. In short, the conductive materials should not be thought of as grounded, but instead as conductive surfaces of low impedance.
In terms of the excitation boundary conditions, the connection between the coaxial transmission line and the source is modeled via the Lumped Port boundary condition, of type Coaxial Cable, with the Source type set to Power. The condition is applied at the annular boundary between the inner and outer conductor. Any other type of transverse electromagnetic (TEM) transmission line could also be modeled, as described in our Learning Center article “Modeling TEM and Quasi-TEM Transmission Lines”.
The Lumped Port boundary condition models a connection to a lossless transmission line extending to infinity, and adding an excitation to the Lumped Port implies a source at infinity sending a signal down the line and into the modeled domain. Part of that signal is dissipated as heat within the domain and impedance boundary conditions, and the other part is reflected back. What we ultimately want to compute from our model is the dissipated heat. It can also be useful to know how much of the incoming signal is reflected back, which is quantified by the S-parameter.

Losses in the sample of dielectric material at 100 MHz, and arrows showing the electric field.
The model is solved over the entire range of frequencies of interest, 100 kHz–1 GHz, and the S-parameter and total heating of the sample dielectric material are evaluated. At even lower frequencies, though, there will come a point where we are no longer able to compute a solution. This is expected behavior, since the electric field starts to approach the static limit. Because of this, the full-wave formulation is no longer appropriate, and we have to look to other approaches.
Solving via the Electric Currents Interface
At very low frequencies, much lower than 100 kHz, this becomes a problem that can clearly be addressed with the Electric Currents physics interface, which solves for the (scalar) electric potential rather than the (vector) electric field. Let’s investigate how high in frequency we can get with this interface while still obtaining similar results.
Within the Electric Currents physics interface, the boundary conditions are different. To start, there is a Ground boundary condition, which does have a clear interpretation as you approach the static limit: it implies that the integral of the electric field along any path between two points on that boundary is zero. For a detailed discussion about the DC case, see our blog post “Do Voltage and Ground Exist?”. Although we know this Ground boundary condition is unphysical at very high frequencies, we will still use it and see how well it agrees with the electromagnetic wave solution as we go up in frequency. The Ground condition is applied on all of the surfaces of the outer conductor, the cavity walls, and the surface that connects the two.
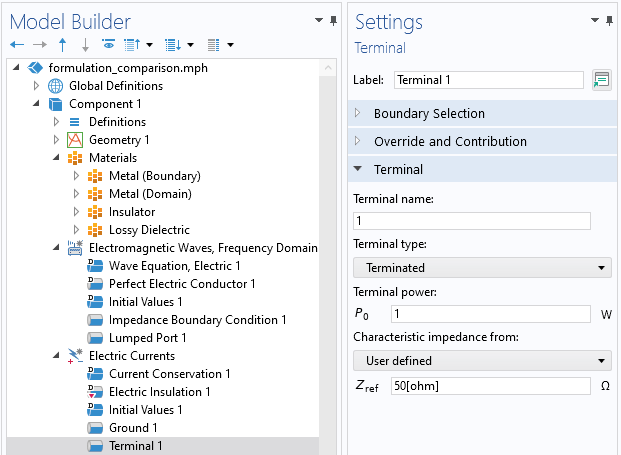
The COMSOL Multiphysics® UI, showing the Terminal > Terminated type.
The surfaces of the inner conductor are excited via the Terminal boundary condition, of type Terminated, which is meant for creating connections to transmission lines of specified impedance, as shown in the figure above. It is analogous in physical interpretation to the Lumped Port used previously in the Electromagnetic Waves interface. The remaining boundary, the annular boundary of the insulator between the inner and outer coax conductor, is set to Electric Insulation. This means that the electric field will be parallel to this boundary, which is the expected solution for the electric field within a coax.
We compare these two approaches in terms of the total losses within the sample material filling the cavity over frequency. The plot below shows that these two models agree over a very wide frequency band; from 100 kHz up to nearly 100 MHz the solutions agree very well. It’s expected that these two approaches will give different results at high enough frequencies, but it is important to note that it can be very difficult to estimate ahead of time at what frequency this occurs. It depends on the geometry, the material properties, and the boundary conditions. In practice, if you are ever in doubt, building two models and comparing results is the recommended approach.

Comparison of the Electromagnetic Waves and Electric Currents physics interfaces. There is an agreement over a wide frequency band.
There is a question that we should have about this model, and that is with regard to one of the assumptions that we made earlier. We had assumed, in the Electromagnetic Wave model, that the skin depth in the metal is small compared to the dimensions of the conductors. This motivated us to assume that the fields inside of the volume of the metal domains were uniform and therefore did not need to be solved. Because of this, we modeled the metal domains via boundary conditions in both of our previous models. In this next example, we can check to see if this assumption was correct and also solve for the skin effect within the conductors.
Solving via the Magnetic and Electric Fields Physics Interface
For this third approach, we use the Magnetic and Electric Fields physics interface. This interface can, roughly speaking, be considered a combination of the previous two interfaces, although more formally it’s known as the A-V formulation and has a unique definition of the electric fields, as described in more detail in our blog post “What Is Gauge Fixing? A Theoretical Introduction”. From a computational-complexity point of view, it’s the most expensive — it solves for both a scalar electric potential field and a magnetic vector potential field in all domains, and the metallic domains would require a boundary layer mesh if we want to solve at frequencies where the skin depth is very small. Here, we will avoid boundary layer meshing, and only address the 100 kHz–1 MHz frequency range. If we get agreement in this range, it’s reasonable to extrapolate that the other, less computationally intensive approaches, are appropriate.
With respect to the boundary conditions, we can again use the Impedance boundary condition on the walls of the cylinder. The remaining boundaries, at the cross section of the coax, are all of the Magnetic Insulation type, meaning that the magnetic field will be parallel to those boundaries and that the electric field will have no component tangential to the boundary. The Magnetic Insulation boundary condition includes subfeatures that additionally specify the conditions on the component of the electric field that is normal to the boundary.
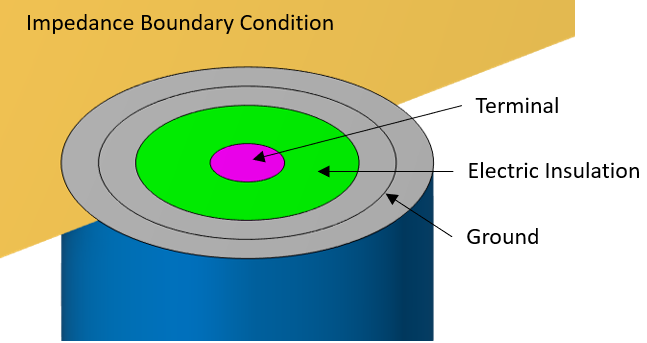
Schematic of the boundary conditions in the Magnetic and Electric Fields interface.
We first use the Terminal condition of type Terminated on the boundary of the inner conductor, similarly to as in the Electric Currents physics interface. Next, Electric Insulation is used on the boundary of the insulator inside of the coax, and lastly, the Ground condition is used on the annular boundary of the outer conductor as well as the surrounding annular boundary of the insulation on the outside of the coax. This completes the electrical connection between the cavity walls and the outer conductor.

Comparison of the other interfaces versus the Magnetic and Electric Fields interface approach over a reduced frequency range.
We solve this from 100 kHz–1 MHz and compare it to the previous results, as shown in the figure above. We see near-perfect agreement, and are thus justified in saying that the approaches of using either the Electric Currents physics interface or Electromagnetic Waves physics interface are equivalent and usually superior since they are less computationally expensive. Via the Magnetic and Electric Fields model we can apply boundary conditions in terms of voltage and ground, with proper understanding of the interpretation of these terms at non-zero frequencies, and additionally extract the losses in the metal domains. This data confirms the assumption that the losses in the metal are relatively small compared to the losses within the dielectric material filling the cavity. It also further validates the other approaches.
Two Other Approaches
We have now shown three different modeling approaches that produce the same results over a range of frequencies. Let’s now look at two more approaches.
The first modeling approach of using the Electromagnetic Waves, Frequency Domain physics interface can be exactly reproduced in the Magnetic Fields physics interface within the AC/DC Module. This interface offers the same boundary conditions, Impedance and Lumped Port. The Magnetic Insulation boundary condition in the Magnetic Fields interface is functionally identical to the Perfect Electric Conductor boundary condition of the Electromagnetic Waves interface. These two physics interfaces will give the same results for this particular problem. This raises the question of why we should use the Electromagnetic Waves, Frequency Domain interface instead of the Magnetic Fields interface.
The distinction between the two arises when different boundary conditions need to be applied. The case we are considering here is of electromagnetic waves that are confined within a cavity, and energy can only enter or leave this cavity through the transmission line feed. (This phenomena is included in the Lumped Port feature.) This particular case can be handled equivalently between the two interfaces. If we instead want to consider a situation where the electromagnetic waves are not confined or completely dissipated within the domain, but can radiate toward the surroundings, then the modeling domain needs to be truncated with a set of nonreflecting conditions that are unique to the Electromagnetic Waves physics interface. We can use the Scattering boundary conditions, or alternatively the Perfectly Matched Layer domain condition, to model a nonreflecting boundary, as described in our blog post “Using Perfectly Matched Layers and Scattering Boundary Conditions for Wave Electromagnetics Problems”.
It’s also worth noting that, in either the Electromagnetic Waves, Frequency Domain physics interface or the Magnetic Fields physics interface, we could solve for the fields and losses within the metallic domains and get the same kind of solution as we got from the Magnetic and Electric Fields physics interface, over the 100 kHz–1 MHz frequency range. This raises the question of why we should use the Magnetic and Electric Fields physics interface at all. Its advantage is over lower frequencies, 100 kHz and below, in models where there might be significant induction currents. As we’ve seen for this particular model, the solution is well characterized by considering only the conduction and displacement currents, as computed from the Electric Currents physics interface.
Finally, let’s take a second look at our approach via the Electric Currents physics interface and see if we can make it even simpler. We were modeling the electric fields and currents in the insulator and lossy dielectric material, but let’s now see if we can ignore the fields in the insulator. Although there are displacement currents in the insulator, these currents are not very significant, especially at lower frequencies. That is, our Electric Currents model could be solved solely in the sample dielectric material, if the frequency range is low enough. The boundaries of the insulator material will now, by default, all be Electric Insulation.
The plot below shows the comparison between all five approaches, and we can see that the simplest approach gives us essentially identical solutions to the other approaches over a wide frequency band, at reduced computational cost.

Comparison of all five approaches.
Closing Remarks
The model developed here illustrates a useful result: that different physics interfaces for solving Maxwell’s equations can produce nearly identical results over wide frequency ranges for certain problem types. It’s important to note that the regime of overlap between these interfaces is strongly dependent on the material properties, the boundary conditions, and the geometry involved.
When you are faced with the question of which electromagnetic physics interface to use, the takeaway is that you will want to compare several different approaches, similar to how we did it here. The advantage to doing so is that you can often find a more computationally efficient approach for your simulation needs.
The model supplementing this article is available for download from the Application Gallery:





Comments (2)
Mohammad Alasmar
May 31, 2023Thank you very much for the detailed explanation.
viccarcel09 Margaret
September 30, 2023What a fabulous post this has been. Never seen this kind of useful post. I am grateful to you and expect more number of posts like these. Thank you very much.