When Marshmallows Become Rock-hard
News | Posted on February 25th, 2013 by Valerio Marra
A while back, I bought a bag of marshmallows, indulged a bit, and then forgot about the opened bag for a few weeks. To my surprise, and disappointment, when my marshmallows cravings returned the top ones were rock-hard while the bottom ones were almost as soft as when I bought them. Why was this the case? By leaving the bag open, water had migrated from the marshmallows into the air.
Open bag of marshmallows.
What’s the Diffusion Coefficient of Water in a Bag of Marshmallows?
Finding my open bag of partially dried-out marshmallows raised the question: what is the diffusion coefficient of water inside the marshmallows bag? I realized that this could be answered by observing what happened to the open bag of marshmallows on my counter; I knew the geometry of the bag, what day it was opened, and I assumed that the “marshmallow water content profile” after 30 days was a straight line. This was the experimental profile I used to set up a mass transport by diffusion simulation with the goal of deducing the diffusion coefficient of water in the bag of marshmallows (hereon referred to as Diff).
Note: In order to find the value of water content at each end of the experimental profile, I needed the water concentration values of both the air and the fresh marshmallows. The former can be derived by knowing that the absolute humidity of air with a relative humidity of 30% at 20°C is ≈5.2 g/m3, which corresponds to a water concentration ≈0.3 mol/m3. While for the latter, I had to do some research and decided to use the data provided here, corresponding to a water concentration of ≈7,781 mol/m3.
Simulating Mass Transport by Diffusion
The initial water concentration in the bag is 7,781 mol/m3 while its value at the open end of the bag is 0.3 mol/m3. In the figure below the geometry is shown that is used for the simulation along with the line where the experimental profile will be compared with the simulations for Diff.
 |
 |
Marshmallow bag geometry and profile line along which the simulated water concentration is compared to the experimental profile.
I ran the simulation for different values of Diff, expressed in m2/s, and compared the results to the experimental profile (see plot below). The value of Diff that best fit the experimental profile was 2·10-9 m2/s.
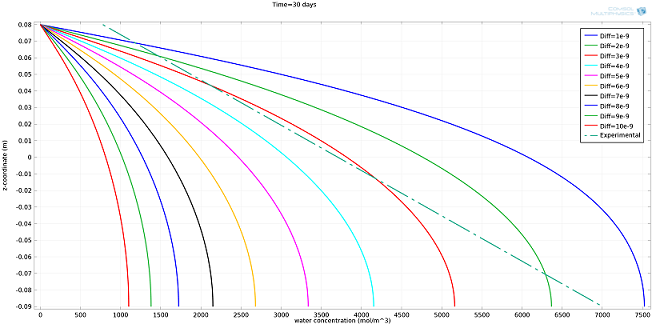
Simulated water concentration vs. experimental profile.
 |
 |
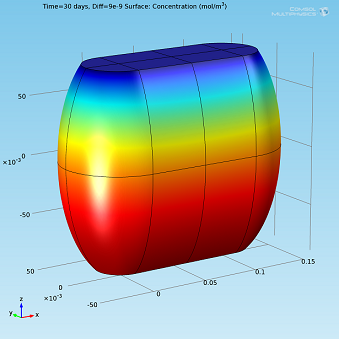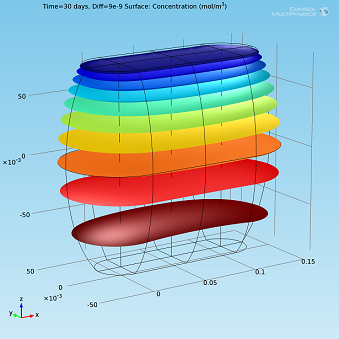
Isosurfaces and surface plots of water concentration for Diff=2·10-9 m2/s.
Discussion and Next Steps
Even if I had to rely on several simplifying assumptions — an experimental profile determined “by hand”, a diffusion coefficient independent from water concentration, time, shape and packing of the marshmallows, chemical reactions and constant boundary conditions — I’ve been able to establish the order of magnitude of the diffusion coefficient and started to understand more about what is happening.
I might even try different bag shapes to find out which shape is less prone to dry out the marshmallows. The next step could also be to include all the effects that I’ve neglected here in a new simulation that would accurately answer the question: how long does it take to dry all the marshmallows out?
Well, in my case, after a couple of months, a quarter of the bag is still edible. You can start from the information provided in this post, run your simulation, and let me know when the last marshmallow will be as hard as a rock!
Further Reading
There’s a lot of applied physics at work when cooking food. If you’re intrigued by this, check out the following resources:
Plenty of simulations related to the food industry have also been presented at the COMSOL Conference over the years. Here are some that grabbed my attention:
- Studying how to dry potato slices
- Dehydration of mushrooms
- Preserving food from deterioration
- How salt diffuses in bacon
Login to Comment
- Login
- Create Account
- Forgot your password?
