4 Examples of Fuel Cell Modeling in COMSOL Multiphysics^®

Fuel cells are one of the most talked about new technologies in the clean energy domain. Fuel cells generate electricity via electrochemical reactions involving hydrogen and oxygen, where the sum reaction yields hydrogen oxidation and oxygen reduction. Simply put, if a fuel cell has a steady supply of hydrogen and oxygen, it will generate electricity. Furthermore, the byproduct generated in this process is water, thereby making it a “clean fuel”, which doesn’t generate carbon dioxide or toxic byproducts.

Exploring Different Fuel Cell Designs

The optimal functioning of a fuel cell involves maintaining a balance between the current density distribution in the cell, the feed of the reactants, and the temperature profile. These aspects are usually studied using modeling and simulation. A multiphysics model could also consider possible structural deformation due to thermal expansion. The Fuel Cell & Electrolyzer Module, an add-on product to the COMSOL Multiphysics^® software, enables you to design and model different fuel cells and incorporate all these aspects in a single model. The software offers various multiphysics couplings, such as reacting flow, nonisothermal flow, and so on, which you can implement to get a clear picture of how the cell will function in real-world applications. You can also extend these studies to entire fuel cell stacks.

Let’s look at four examples of how COMSOL Multiphysics can be used to evaluate the different aspects of fuel cell designs…

1. Solid Oxide Fuel Cell

The electrolyte and the electrodes are made of metal oxides (hard ceramic materials) in a solid oxide fuel cell. The electrodes in this cell are porous gas diffusion electrodes (GDEs), and the solid electrolyte is included between them to form a sandwich structure. In this section, we’ll explore the inner workings of a solid oxide fuel cell with modeling and simulation using the Current Density Distribution in a Solid Oxide Fuel Cell tutorial model.

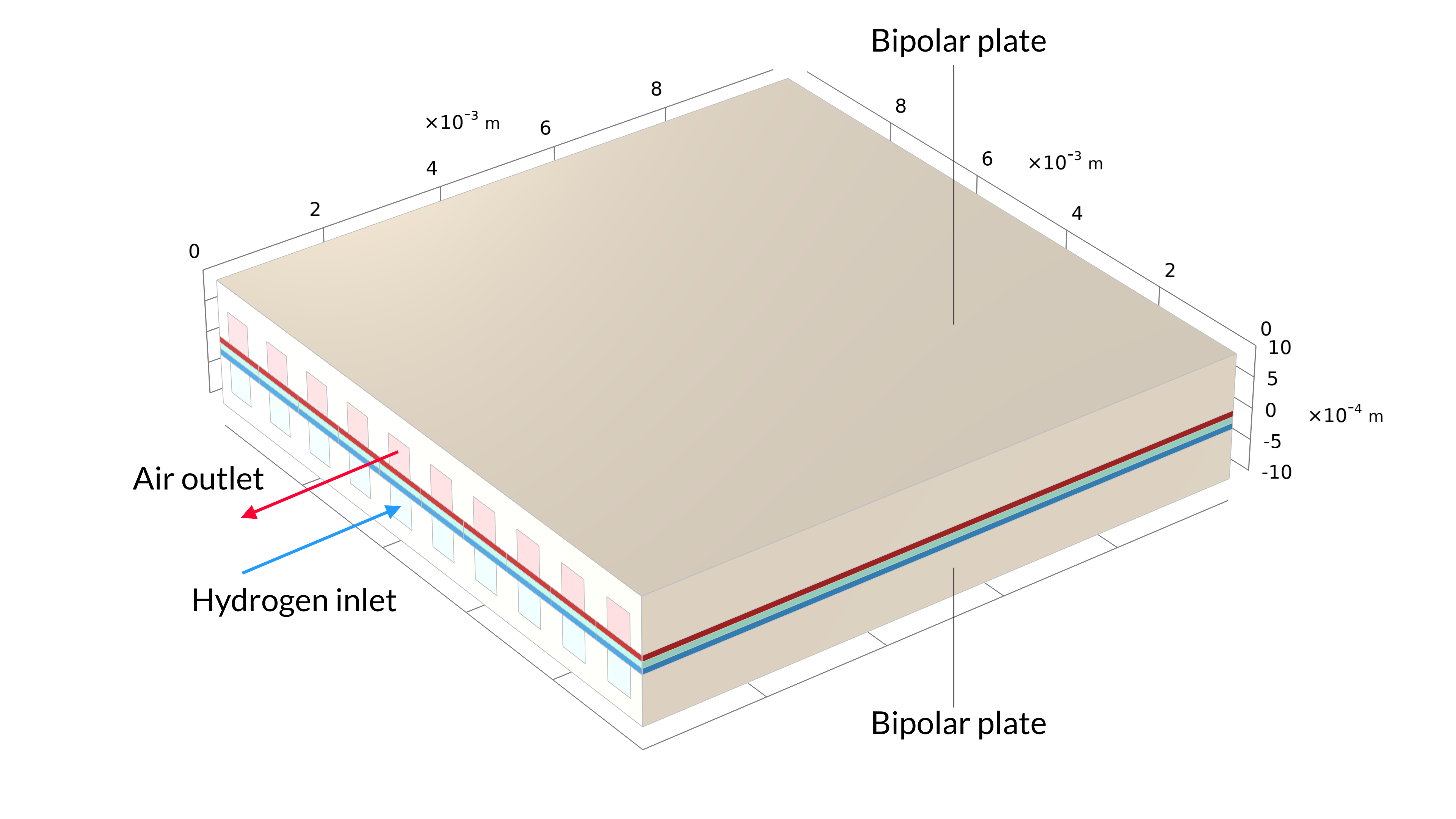
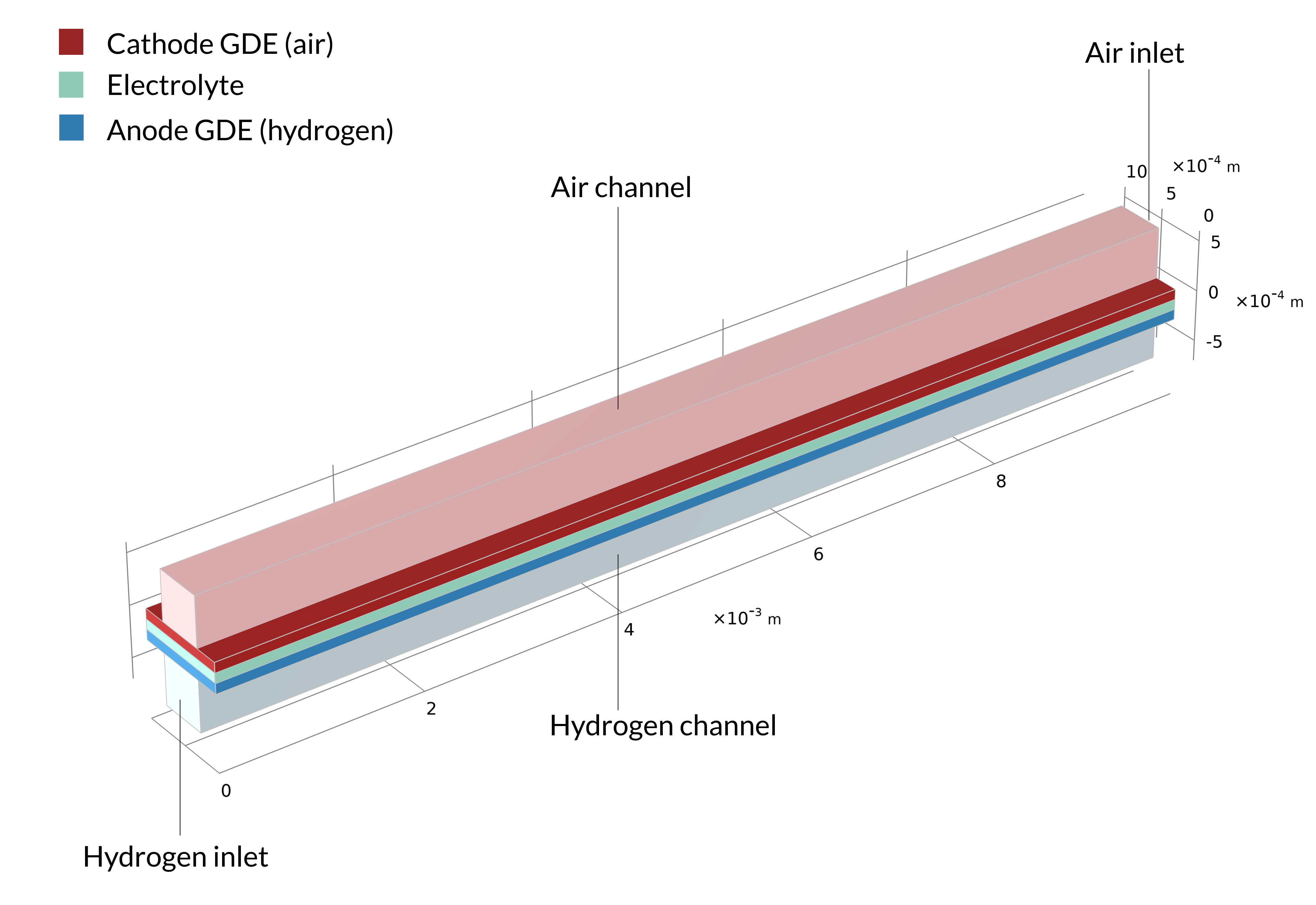
This tutorial can be used to model the current density distribution in a unit cell of a parallel channel solid oxide fuel cell with countercurrent flow. The fuel in this cell is humidified hydrogen gas (hydrogen and water vapor), which enters at the anode side. Humidified air (water vapor, oxygen, and nitrogen) is supplied at the cathode side.

Figure 1. The solid oxide fuel cell geometry of one cell in a stack, including the bipolar plates (left). The model geometry is one unit cell, including one air and one hydrogen channel (right). The bipolar plate is assumed to be at constant electric potential and is not included in the model. Instead, the electric potential is set as a boundary condition at the contact surfaces between the GDEs and bipolar plates.

This model includes a full coupling between:

• Mass balances at the anode and cathode
• The flow in the gas channels
• The gas flow in the porous electrodes
• The balance of the ionic current carried by the oxide ion
• An electronic current balance
• The charge transfer reactions (electrochemical reactions) at the anode and cathode

A truly multiphysics problem, this model involves several physics interfaces describing the processes and phenomena occurring within the cell. Maxwell–Stefan’s diffusion and convection equations describe the material transport in the gas phase, which are solved with the Hydrogen Fuel Cell interface. The flow through the open channels is defined by the compressible Navier–Stokes equations, whereas the Brinkman equations describe the flow velocity within the porous electrodes. The current balance in the electrolyte, pore electrolyte, and electrodes is defined using porous electrode theory, coupling the local concentration in the GDEs with the Nernst equation for thermodynamics and the Butler–Volmer expressions for the charge transfer reaction kinetics (electrode kinetics).

The interesting parameters to investigate in this model is the relation between the:

• Width of the channels
• Thickness of the electrodes
• Conductivity of the electrolyte (including the pore electrolyte)
• Conductivity of the electrodes
• Length of the cell
• Gas composition and gas feed rate

These design and operating parameters decide the cell’s performance at different loads. The model is fully parameterized, which means you can run the simulations for different values of the abovementioned parameters to understand and investigate the cell’s behavior. See a preview of this model’s results in the section below, and then get an in-depth look at how to build it by checking out its related MPH-file and PDF instructions in the Application Gallery.

Modeling Results

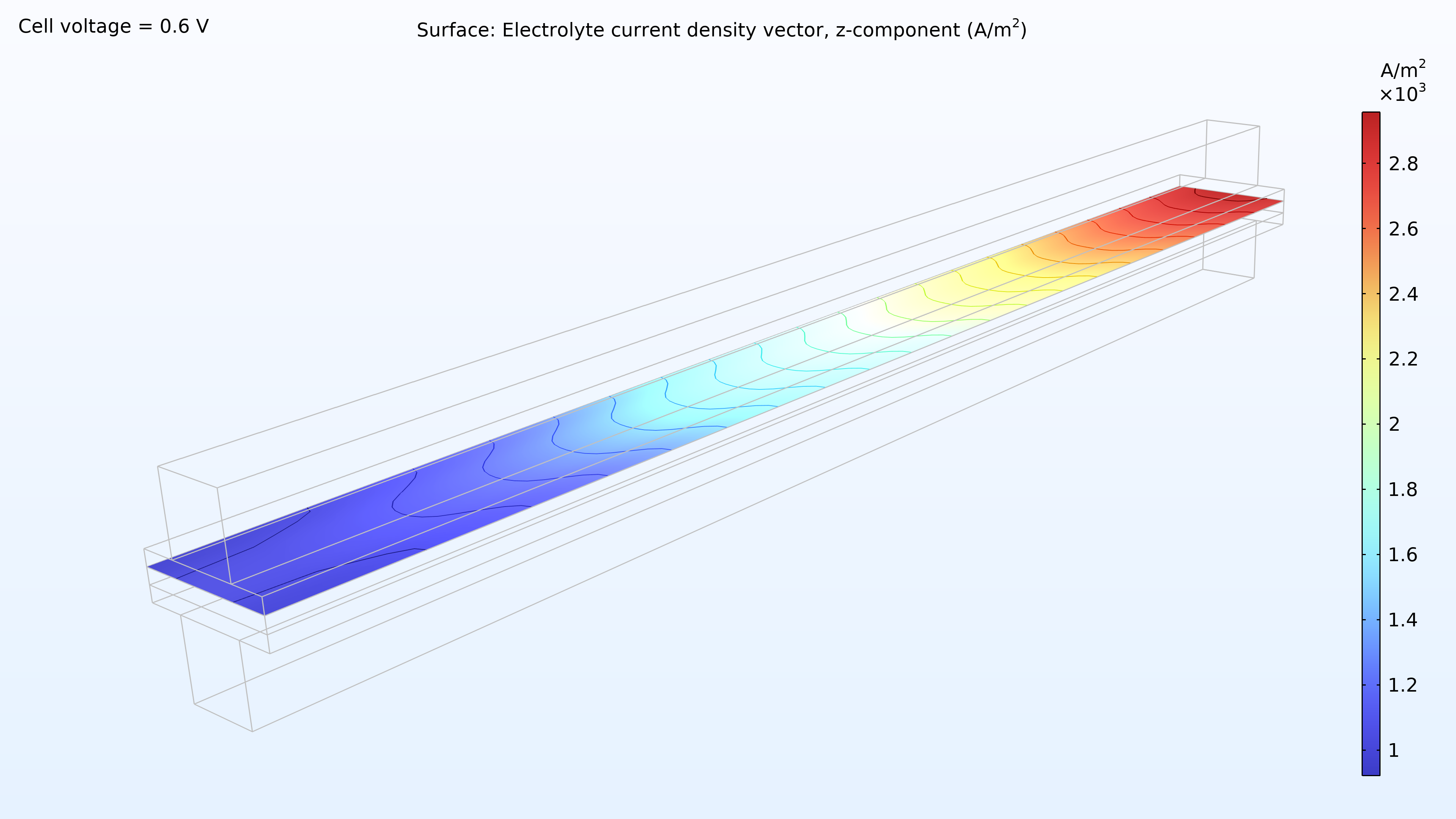
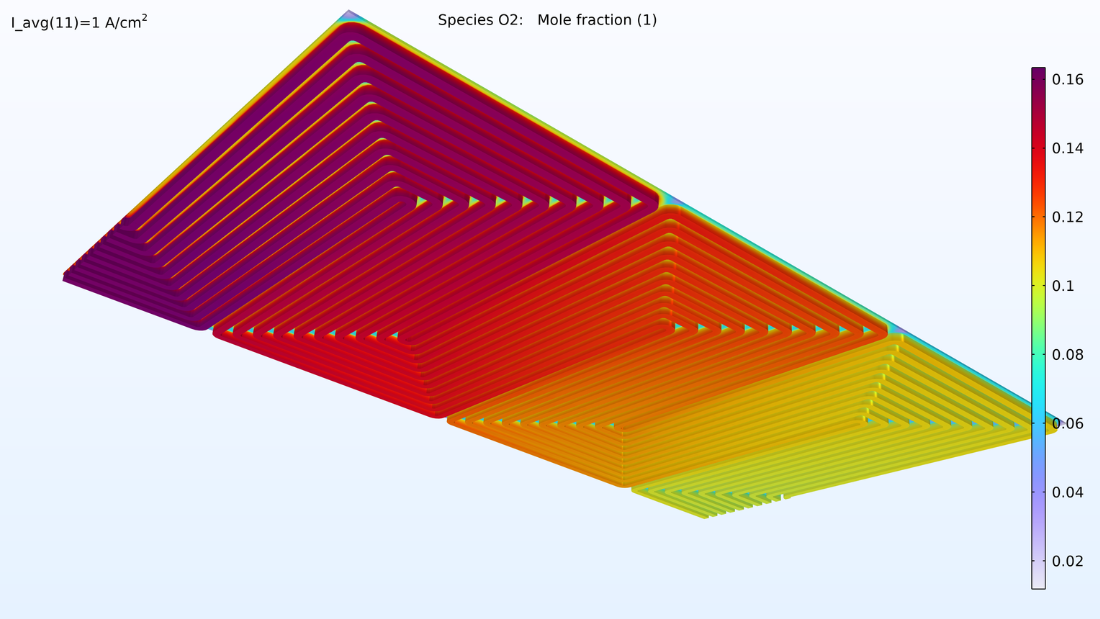
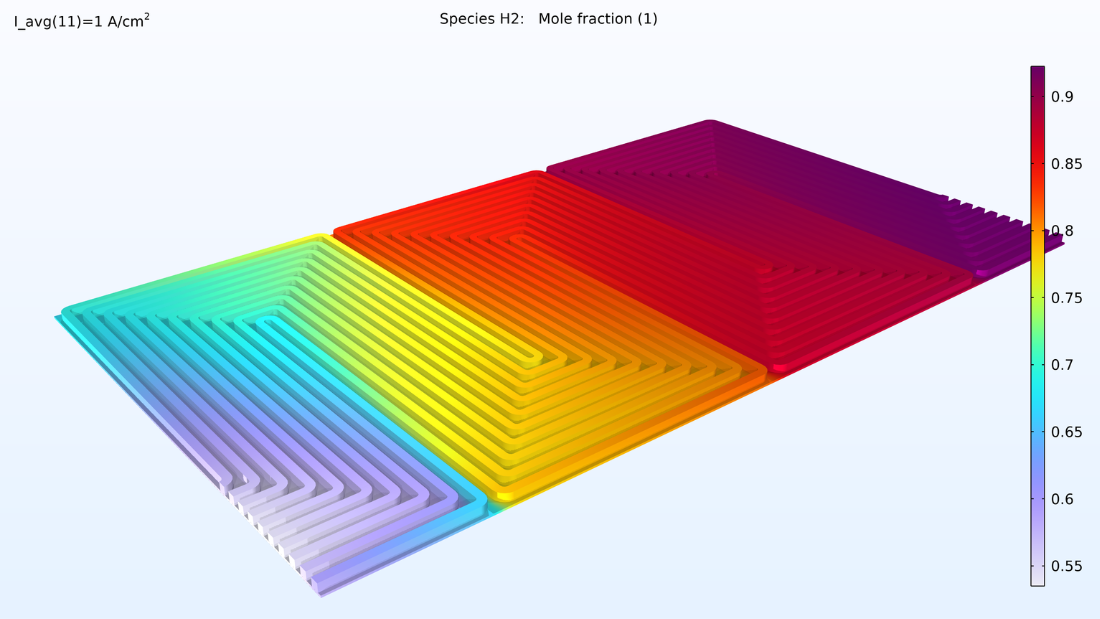
From left to right, the plots in Figure 2 show the hydrogen mole fraction in the anode, the oxygen mole fraction in the cathode, and the current density over the electrolyte. The model shows that the feed of air limits the cell’s performance, resulting in a high current density at the air inlet and a low current density at the air outlet. In addition, we can see that the current density is slightly higher in the middle of the channels compared to the edges, where the current collector and feeder contact surfaces impede the transport of gas.

Figure 2. Plots showing the hydrogen mole fraction at the anode (left) and the oxygen mole fraction at the cathode (middle) at a cell voltage of 0.6 V, with the composition shown in the gas channels and the gas diffusion electrodes. The current density distribution in the electrolyte (right) shows that the air feed limits the cell’s performance, resulting in a high current density at the position of the air inlet.

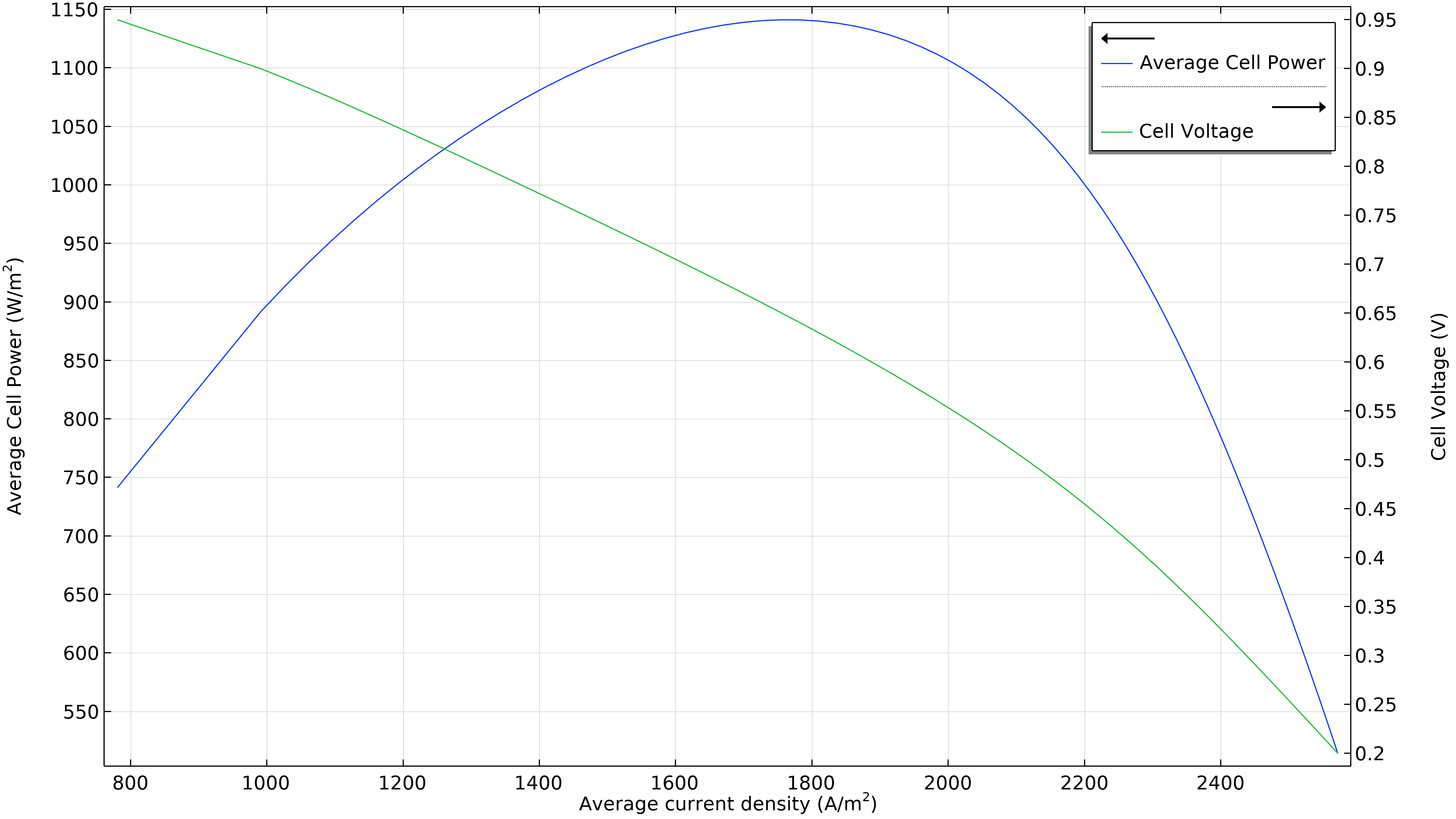
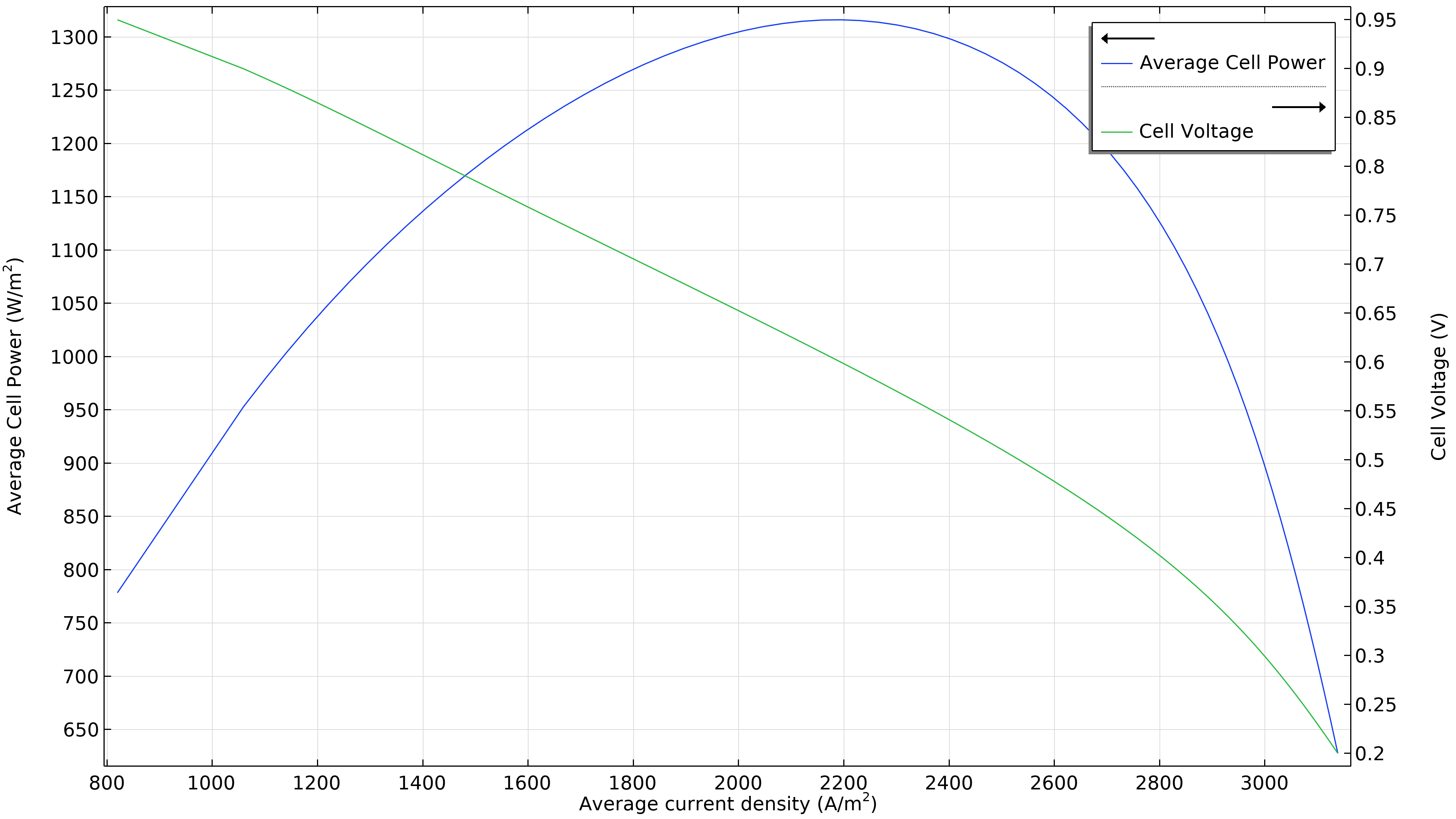
Figure 3 shows that the maximum power at the operating conditions in Figure 2 is at a current density of just under 1800 A/m² (left plot below), resulting in a maximum power of just beneath 1150 W/m². If the airflow rate increases, the maximum power density rises to 1300 W/m² (right plot below). If we were to plot the current density distribution in the electrolyte, we would see that it is substantially more uniform. However, this increased performance has to be balanced with the power required by the air pump, which has to deliver 50 percent higher pressure.

Figure 3. Polarization and power density curves at an air inlet pressure of 6 bars (left), showing a maximum power of just below 1150 W/m² at about 1800 A/m². Increasing the airflow rate by increasing the inlet pressure to 9 bars (right) shifts the maximum towards higher current density (2200 A/m²) and also higher power density (1300 W/m²).

2. Low-Temperature PEM Fuel Cell

Proton exchange membrane (PEM) fuel cells have a polymer membrane as an electrolyte; generally, a proton exchange membrane with a relatively high water content during operation. In the Low-Temperature PEM Fuel Cell with Serpentine Flow Field tutorial model, the membrane electrode assembly (MEA) — consisting of the membrane and the gas diffusion electrodes (GDEs) — is sandwiched between bipolar plates, which include serpentine-shaped gas channels. In the geometry below, the air channels with their inlets are located above the MEA, while the hydrogen channels with their inlets are below the MEA.

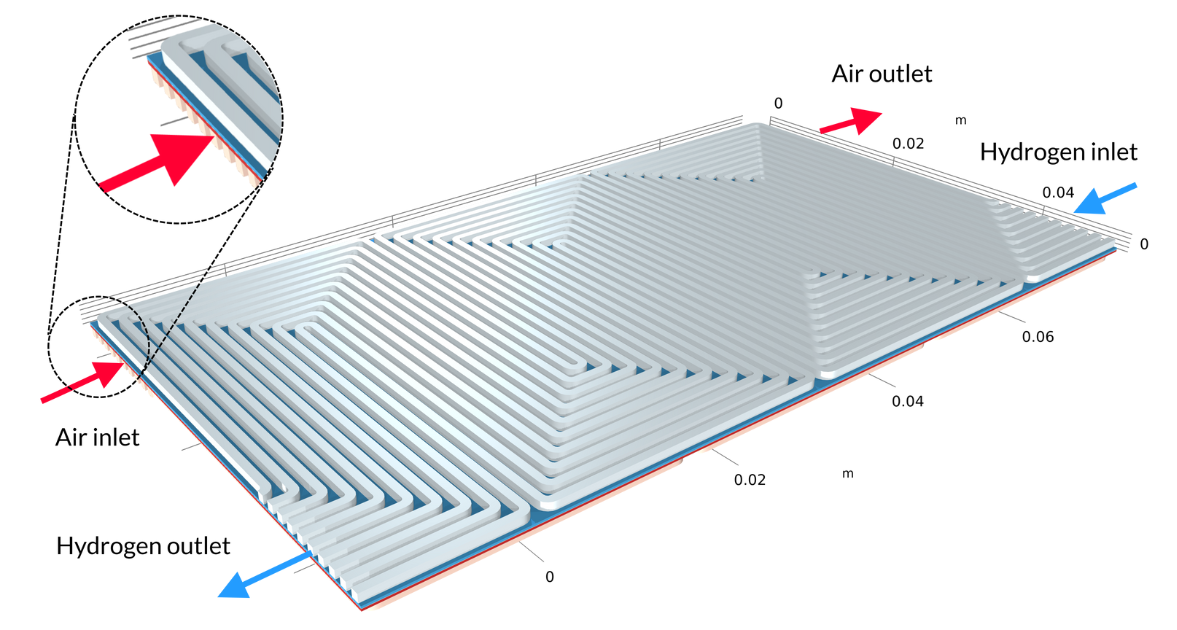
Figure 4. The geometry for the PEM fuel cell model.

The PEM fuel cell produces water at the cathode due to the hydrogen oxidation reaction at the anode (negative electrode) and the oxygen reduction reaction at the cathode (positive electrode). The water produced may permeate through the membrane to the anode side. Suppose water is not removed efficiently from the cathode GDE, where it is produced. In that case, flooding of the electrode pores occurs, which blocks the oxygen supply with a dramatic performance loss as a consequence. In contrast, if the membrane and pore electrolyte become too dry, this results in a low ohmic conductivity in the electrolyte. Therefore, one crucial factor in the operation of a PEM fuel cell is water management.

This model solves for:

• Charge balances and mass transport equations in the gas diffusion electrodes and the membrane electrolyte
• The flow equations in the gas phase on each side of the membrane
• The equations for the transport of water in the membrane via diffusion (permeation) and migration (electroosmotic drag)
• The charge transfer reaction equations (electrochemical reactions) at the electrodes

The interesting aspects to investigate with this model are the:

• Impact of the serpentine pattern
• Dimensions of the channel cross section
• Width of the contact surface between the bipolar plate and the electrodes
• Dimensions of the MEA
• Material properties of all components of the cell

All of these aspects can be studied at different operating conditions (gas feed rates and load). The model can also be used to optimize the cell design for a given gas feed and load. Check out an overview of the modeling results for this model in the section below; if you’d like to jump right into the step-by-step instructions for building this model, you can download them here.

Modeling Results

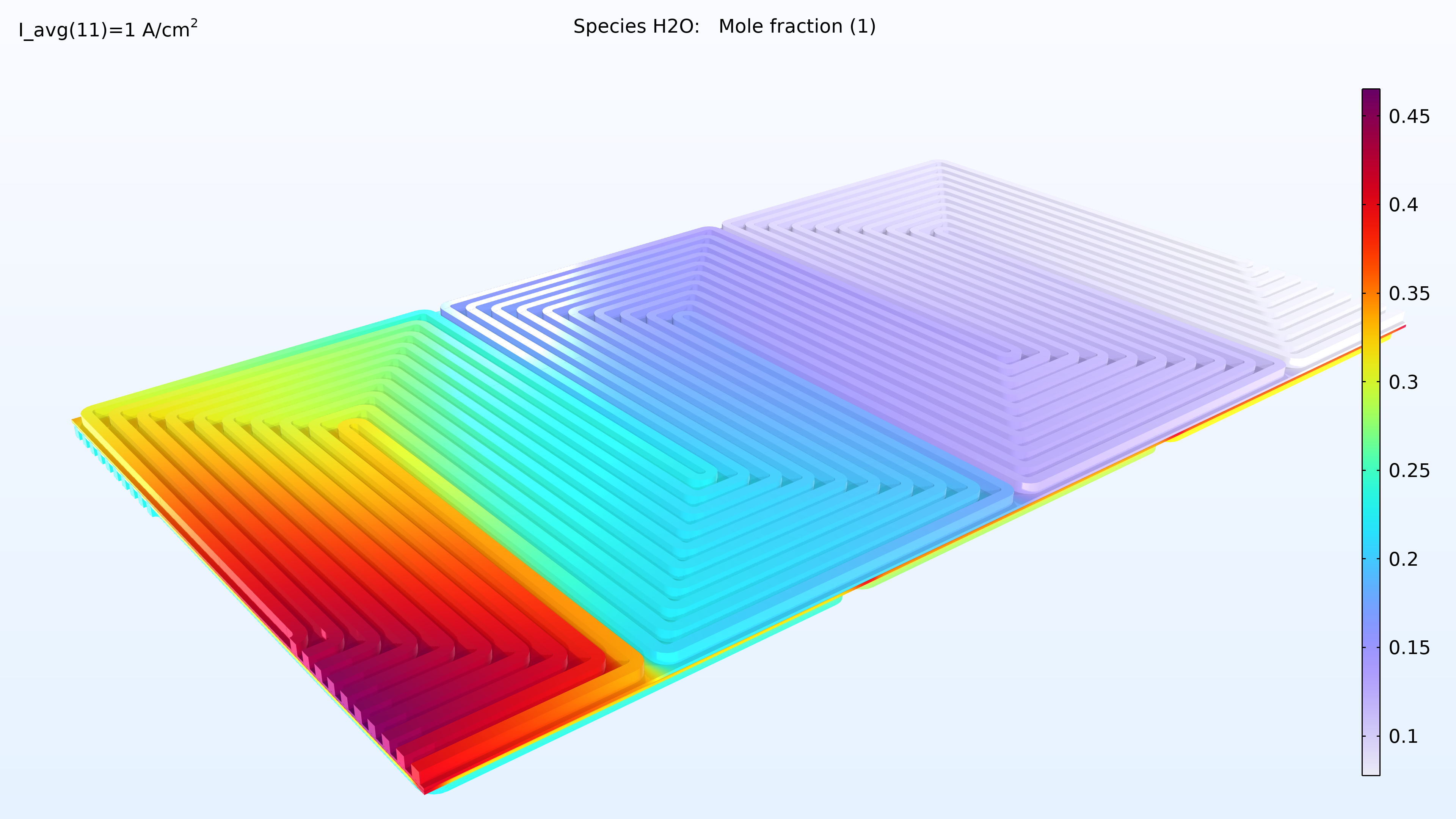
This model computes the composition of the gases in the respective GDEs and gas channels, as shown in the plots in Figure 5. These plots show a substantially larger depletion of oxygen than hydrogen. This depletion occurs along the thickness of the GDE, mainly due to oxygen having smaller diffusivity. Since the flow in the air and hydrogen channels is countercurrent, the two reacting gases are depleted on opposite ends of the bipolar plates.

Figure 5. Plots of the oxygen molar fraction (left) and hydrogen molar fraction (right).

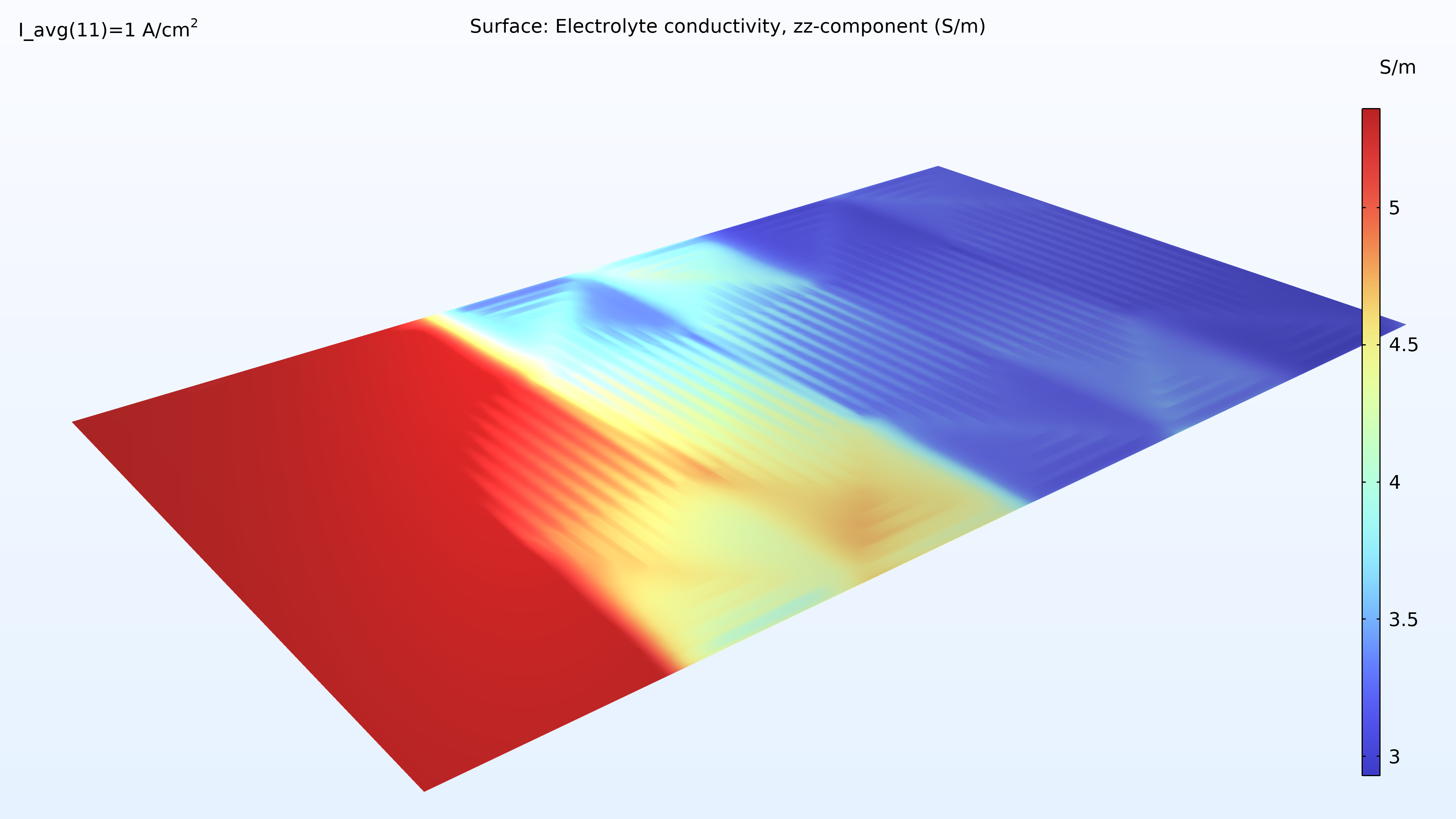
If we look at the water activity in the hydrogen channel and in the membrane, we can see that this activity is larger closer to the air inlet. There is a high oxygen content in the gas phase at this position, resulting in a higher local current density since oxygen transport limits the reaction rate. We can also see that the membrane conductivity is more significant at the position of the large water activity, which impacts the cell’s current density distribution in the cell. The oxygen and the water content increase the current density until the liquid water content in the cathode GDE starts impeding the gas transport.

Figure 6. Plots of the relative humidity in the channels (left) and water activity in the membrane (right).

3. Nonisothermal PEM Fuel Cell

With the Nonisothermal PEM Fuel Cell tutorial model, we can model the intercoupled electrochemical reactions, fluid flow, heat transfer, and charge and species transport in a PEM fuel cell. The cell in this tutorial includes a membrane electrolyte assembly sandwiched between gas diffusion layers (GDLs), which serve as electrodes. The active layers of the electrodes are modeled as surfaces, that is, neglecting their geometrical thickness. (Active layer thickness is a parameter, but it is not reflected as a thickness in the model’s geometry, which means that gas composition and electric potential are constant along the active layers’ thickness.) The hydrogen channels are formed by a corrugated plate that also serves as the current feeder in contact with the anode. Cooling channels, filled with liquid water, run on the other side of the hydrogen channels. The air compartment is formed by an expanded mesh current collector that separates the cathode from a flat metal plate. The metal plate, positioned on top of the expanded mesh, serves as a bipolar plate. It also separates the cathode compartment from the cooling channels of the next cell, which would be repeated above the current one in a stack.

Note that Figure 7 is two units in width; it contains two hydrogen channels. Due to symmetry along the width, we would only need to model 1/4 of this geometry. However, since such results are difficult to interpret — and since the model equations can be solved in a few minutes — we can use a model with a larger geometry than needed.

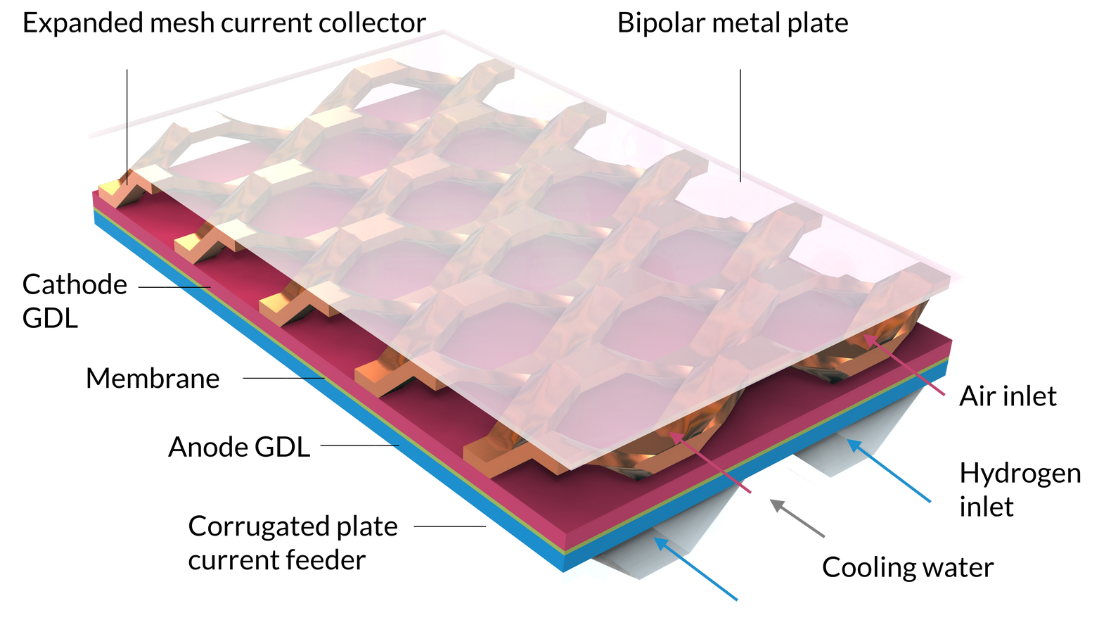
Figure 7. The geometry for the Nonisothermal PEM Fuel Cell tutorial model.

The inlets for the humidified air and hydrogen gas streams, as well as the liquid cooling fluid, can be seen on the right-hand side of the figure.

The cooling liquid water is described using Navier–Stokes equations for laminar flow using the Single Phase Flow interface, while the cell temperature is defined and solved using the Heat Transfer interface. Understanding the entire working of the cell — including the flow, chemical species transport, electrochemical reactions, and heat transfer through the cell — involves various multiphysics phenomena, which are defined using the following multiphysics nodes in the model: Reacting Flow, Electrochemical Heating, and Nonisothermal Flow.

The impact of the expanded mesh structure used in the air channel is interesting to study here. The purpose of this structure is to create a flow field component perpendicular to the MEA. This allows for oxygen supply and water removal. The fuel cell’s performance may vary with the parameters that govern the expanded mesh geometry. Such parameters may influence the relation between the current collector contact with the electrode and the area available for mass transport, including water removal. The model allows for the optimization of the structure for the given operating conditions and the load. See an overview of this model’s results below, then learn how to build it yourself by downloading the PDF documentation and MPH-file from the Application Gallery.

Modeling Results

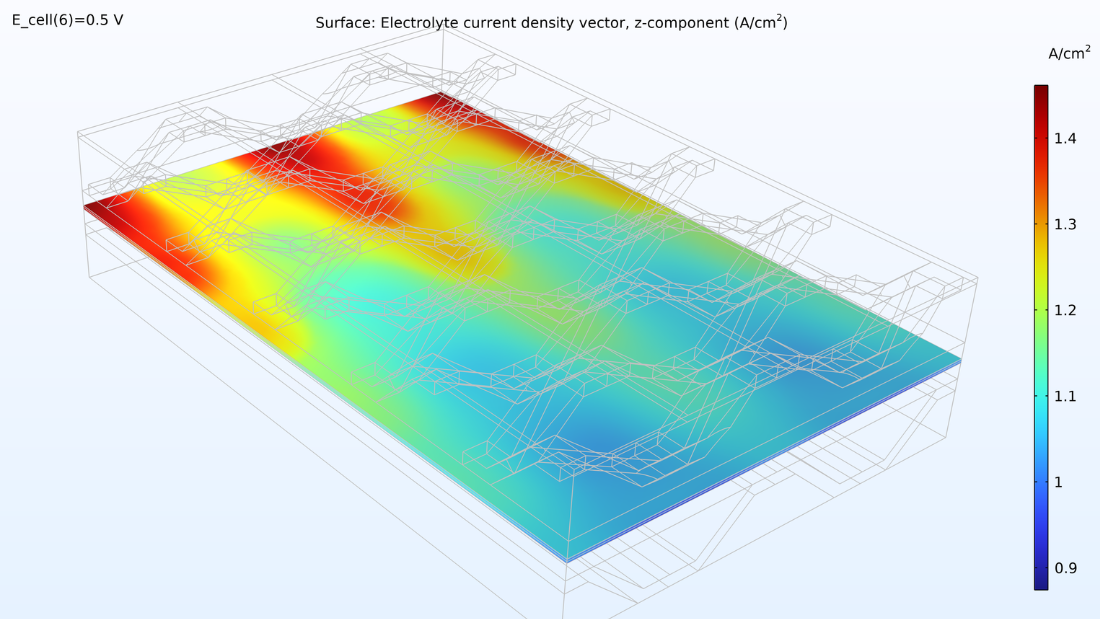
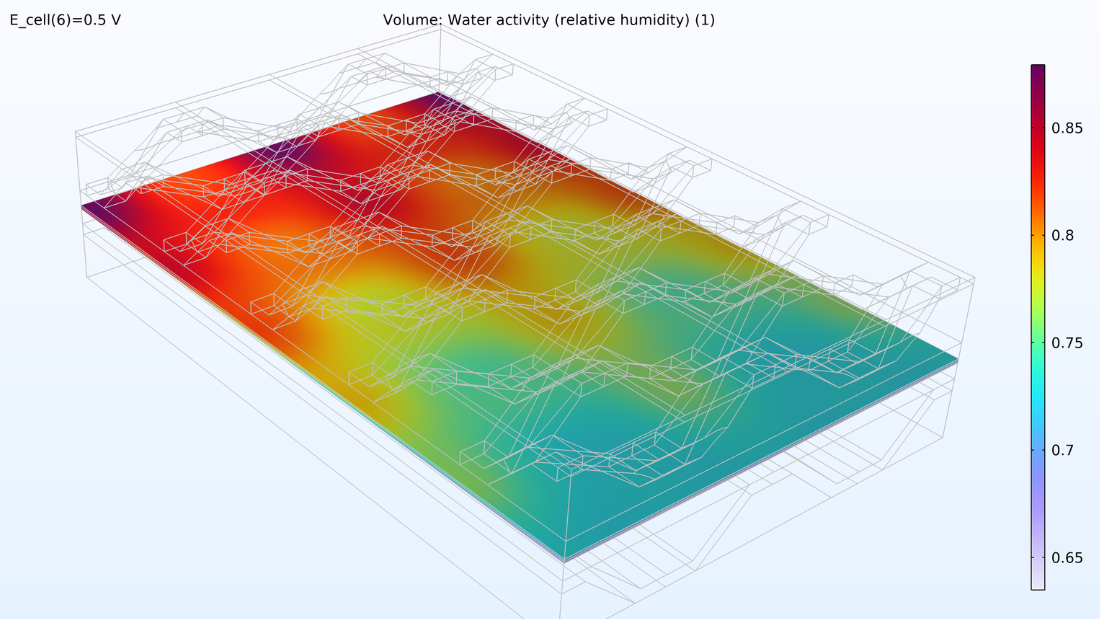
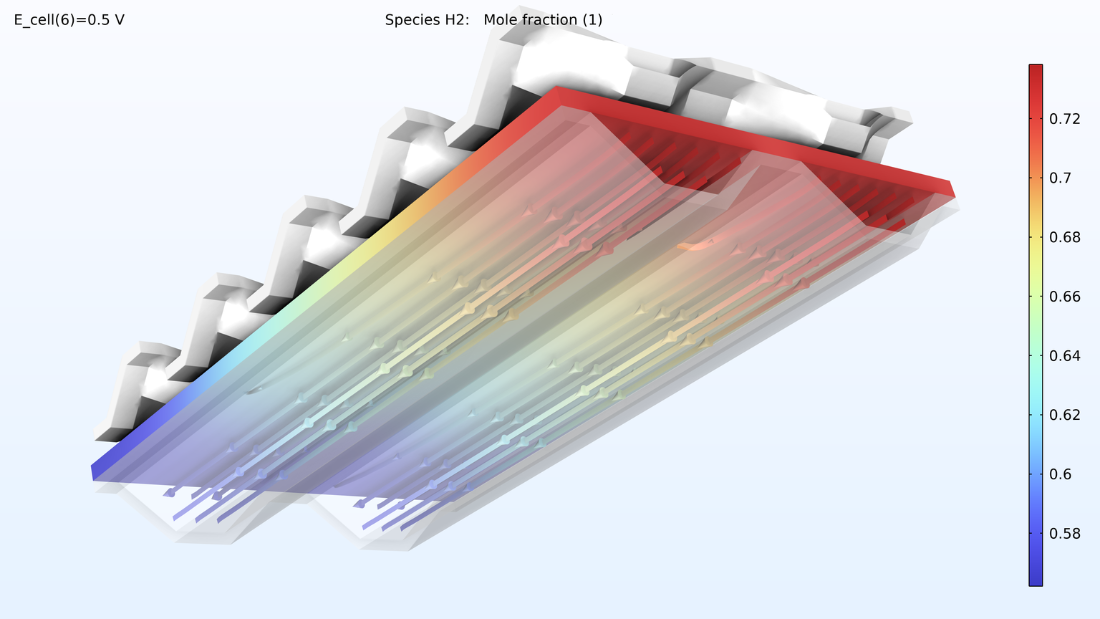
At left, the plot below shows the electrolyte current density of the membrane, where the current density increases toward the outlet side. This is due to the conductivity of the membrane, which increases with its water content due to the formation of water. If we look at the water content in the membrane, we can see that water accumulates below the contact areas between the current collector and the cathode, where the current density is also large. This could eventually become a problem if water floods the cathode, impeding the transport of oxygen. Suppose we elongate the cell by making the hydrogen channels twice as long while keeping the operating conditions constant. In that case, we would eventually see a dramatic decrease in the current density along the length of the channels as the oxygen reduction reaction is slowed down due to mass transport limitations.

Figure 8. The through-plane electrolyte current density of the membrane (left) and relative humidity of the membrane (right) at a cell voltage of 0.5 V.

With this model, we can also observe the oxygen molar fraction and the water vapor molar fraction in a cathode gas mixture. The oxygen levels decrease toward the outlet while the water levels increase.

Figure 9. Plots of the oxygen molar fraction (left) and hydrogen molar fraction (right).

In addition, the temperature profile of the whole cell and the cooling channel can be seen. The highest temperatures are observed in the MEA, which makes sense because it is where we find the heat sources through Joule heating and activation losses.

Figure 10. Temperature distribution in the cell.

The power dissipation in the cell is shown in Figure 11. This plot shows the distribution of heat generation in the cell. We can see that the most significant heat source is in the membrane, which is due to the poor conductivity of the membrane. In addition, we can see a substantial generation of heat at the position where the expanded mesh makes contact with the cathode. Here, the conductivity of the electrode is relatively poor (compared to the current collectors), while the current density is high.

Figure 11. A logarithmic plot of the heat sources in the MEA, current feeder, and current collector.

Lastly, we can generate a polarization curve for the cell showing the cell voltage as a function of the average current density (current per unit membrane area). The significant decrease in cell voltage at low current density is due to activation overpotential, mainly at the cathode. At the same time, a linear region dominated by ohmic losses follows at slightly higher current densities. We see a slight increase in losses at high current densities, where the curve bends slightly downwards due to mass transport resistance.

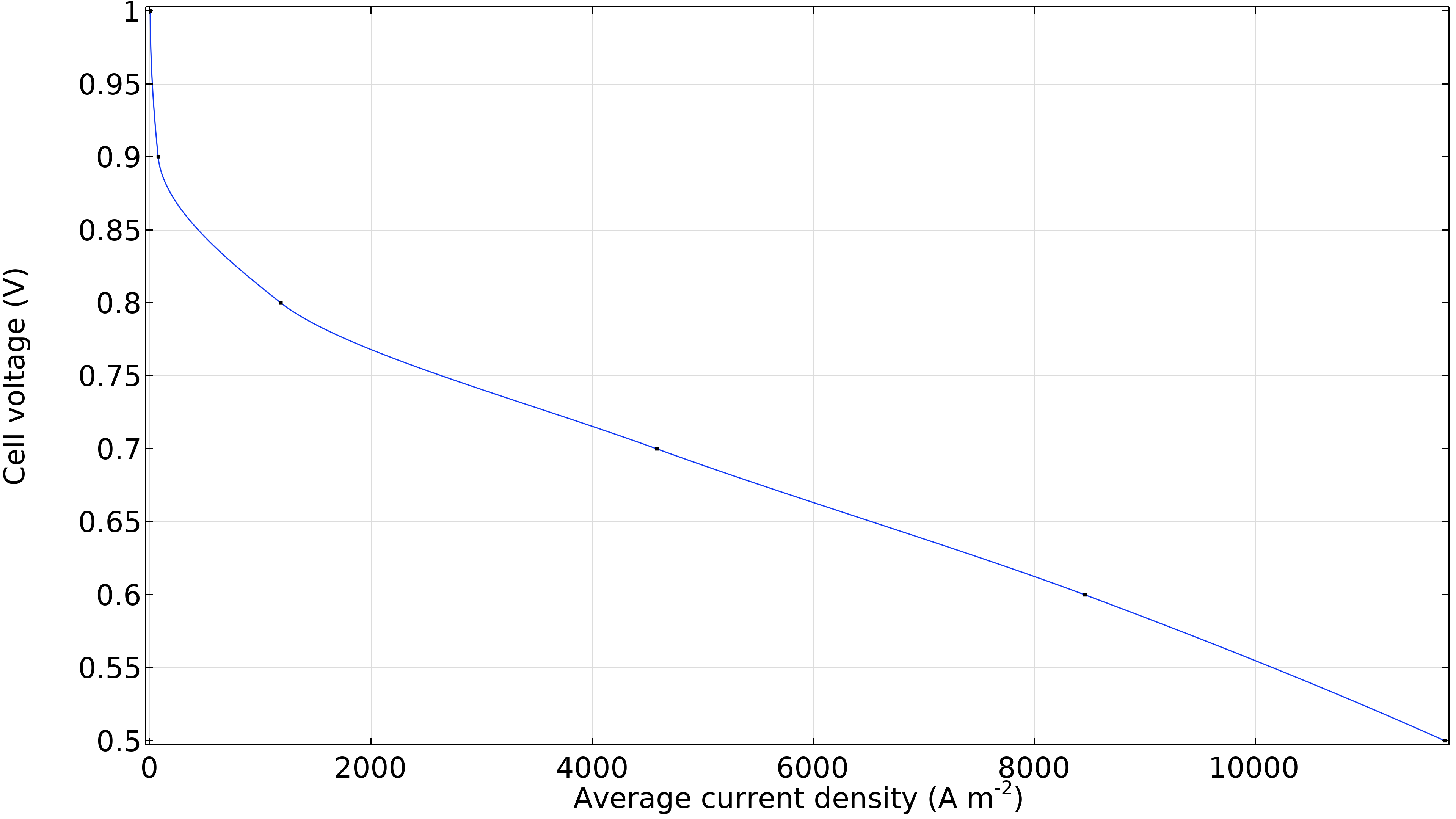
Figure 12. Polarization curve showing the cell voltage as a function of the average current density.

4. Fuel Cell Stack Cooling

The Fuel Cell Stack Cooling tutorial model, introduced in COMSOL Multiphysics version 6.1, can be used to evaluate the thermal management of a PEM fuel cell stack consisting of five cells, five MEAs, and two end plates. This type of analysis is important because an uneven temperature distribution within a fuel cell stack’s cells can result in nonuniform water vapor condensation and an unwanted variation in cell-to-cell performance.

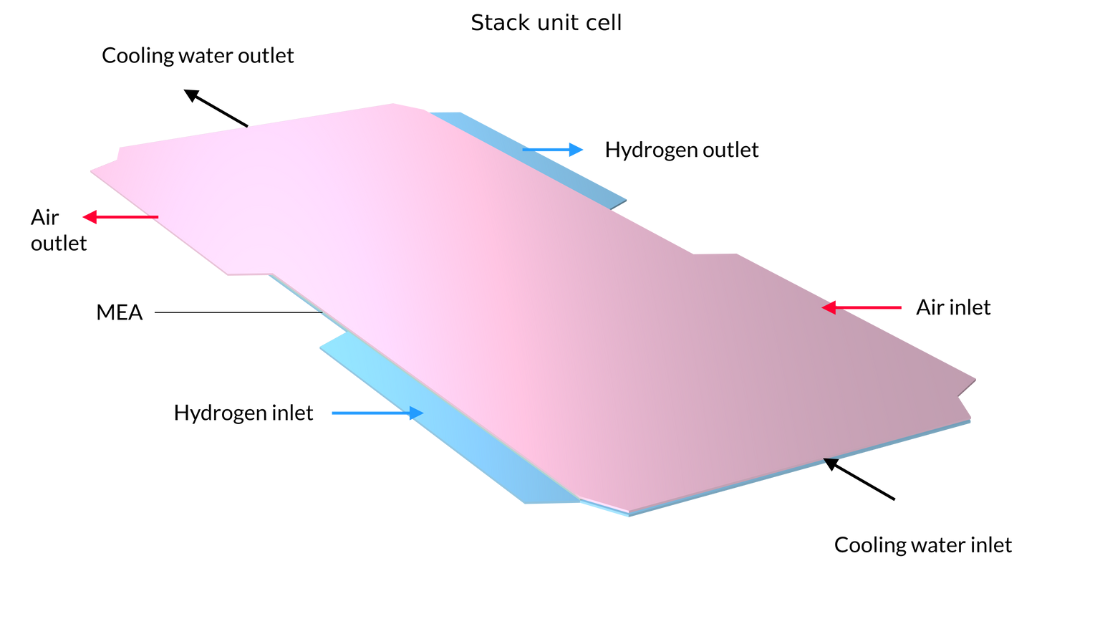
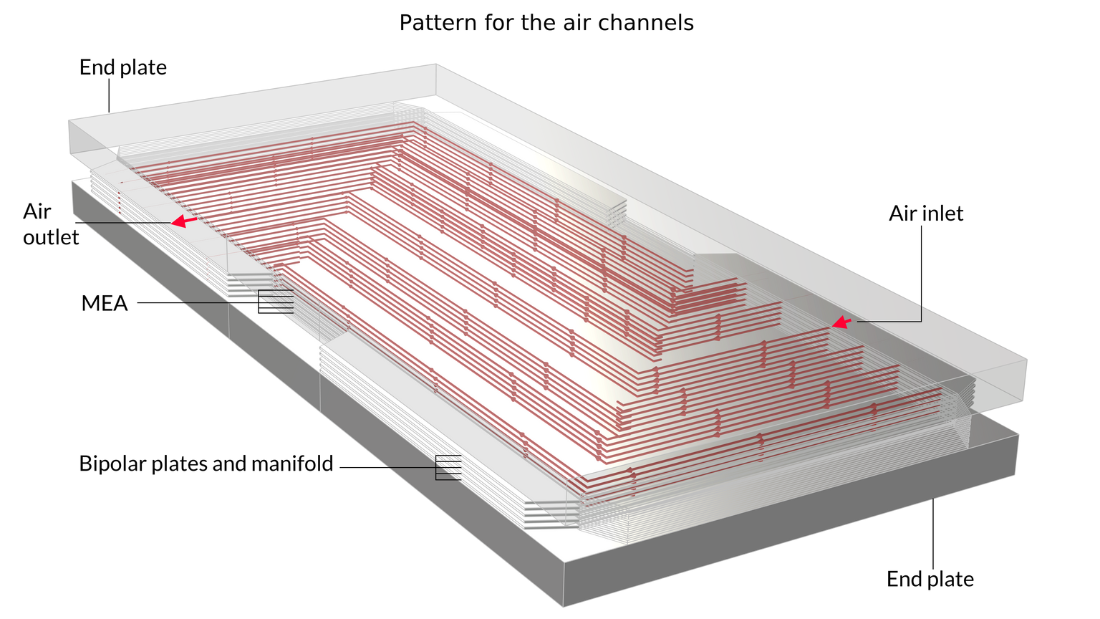
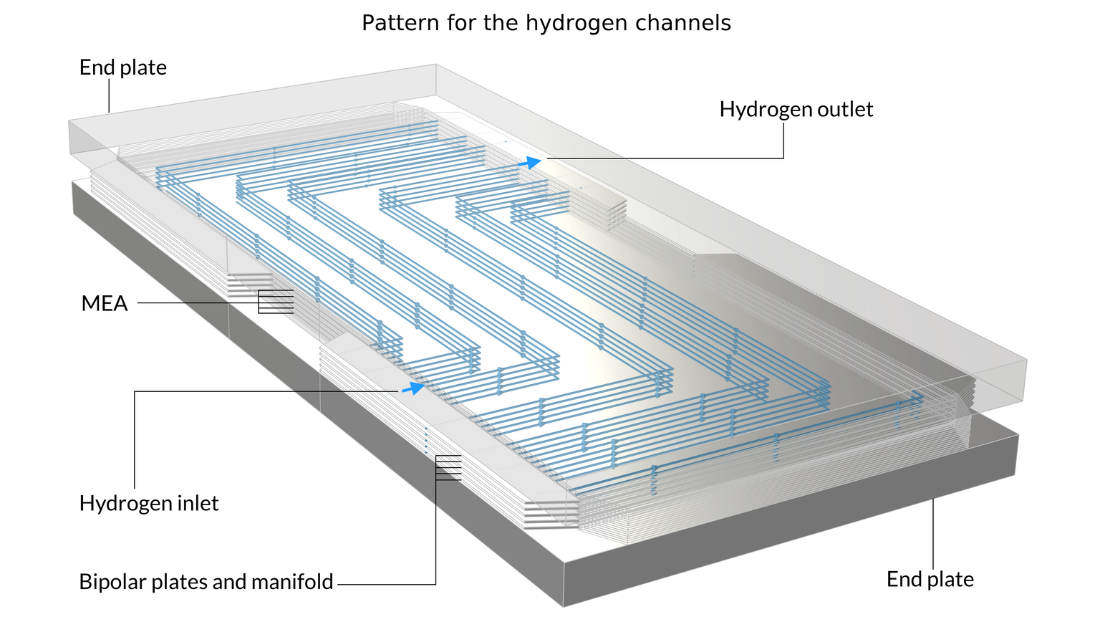
In this example, the stack is interlayered with bipolar plates that carry liquid cooling fluid. The image on the left shows the repetitive unit cell used to help form the model geometry. In contrast, the pictures in the middle and on the right show the final model geometry, which is constructed by sandwiching five stacked unit cells between two metal end blocks.

Figure 13. Here, we can see the repetitive unit cell (left) as well as a view of the stack with 5 unit cells showing the oxygen channel pattern (middle) and the hydrogen channel pattern (right). The metal plates containing the air and hydrogen channels, shown in pink and blue in the figure on the left, are welded back-to-back in the stack. Due to the pattern of the channels, space is left between the welds forming the flow channels for cooling water. The end plates hold the structure and apply pressure to maintain optimal contact between the bipolar plates and the MEA.

The model defines the equations for:

• Temperature
• Electrode and electrolyte phase potentials
• Mass transport of the reacting species in each separate gas compartment
• Fluid pressures and flow fields in the gas and liquid flow compartments
• Electrode kinetics in the active layers of the MEA

The interesting aspects to study in this model are the variations in composition, temperature, and current density distribution that may occur in the stack. These aspects depend on the geometry of the bipolar plates and the MEAs. They may also depend on the number of cells that are included in the stack. The model allows us to treat the geometry of the gas channels using a porous media approach with anisotropic properties that reflect the structure of the gas channels. By comparing such an approach with the full description of the gas channels, we can verify its accuracy. The benefit of this approach is that it gives good accuracy (depending on the purpose) while reducing the computational cost substantially (CPU time and memory requirement).

Browse a few of this model’s results below, then try it out by downloading its PDF instructions and MPH-file in the Application Gallery.

Modeling Results

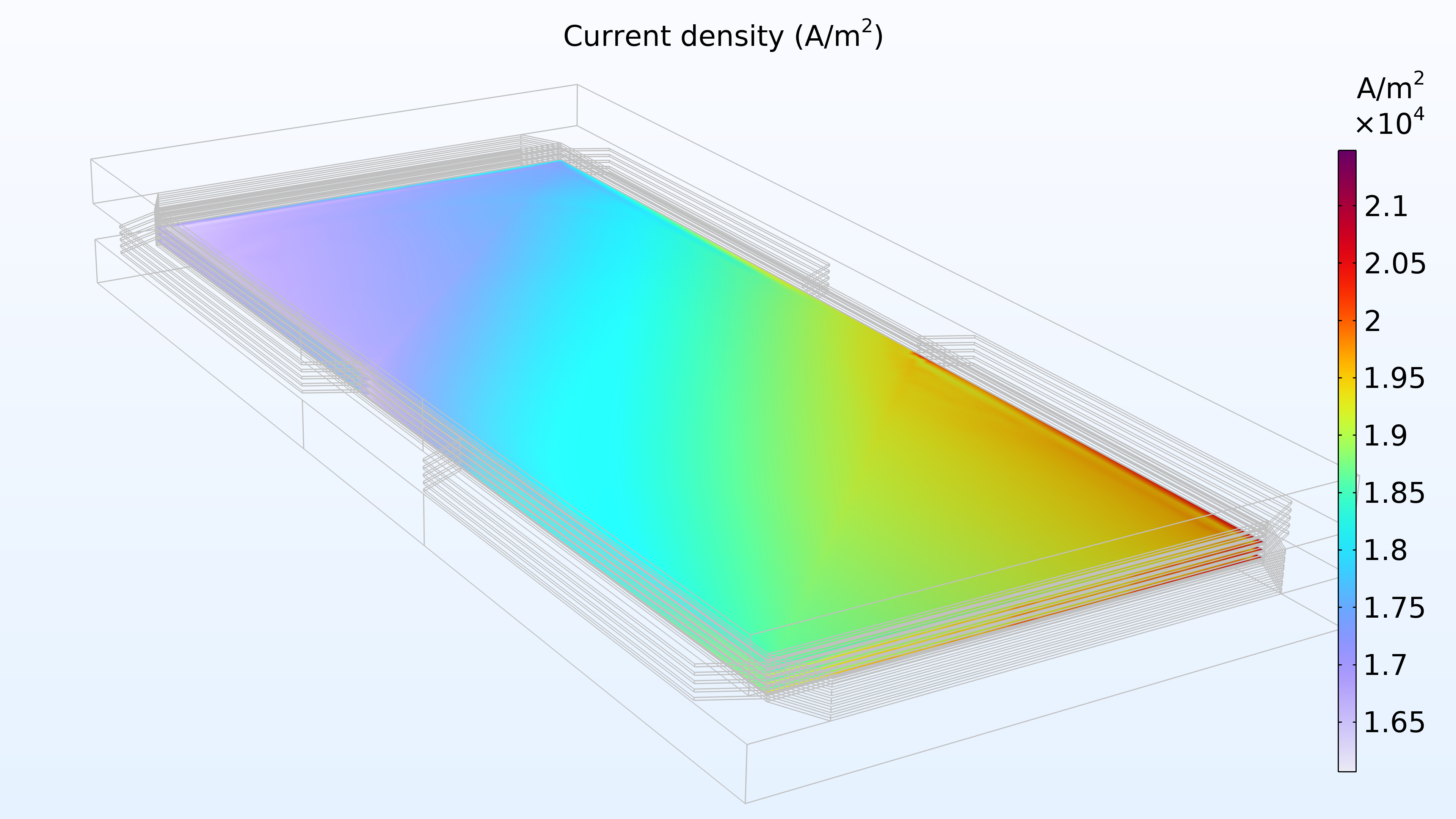
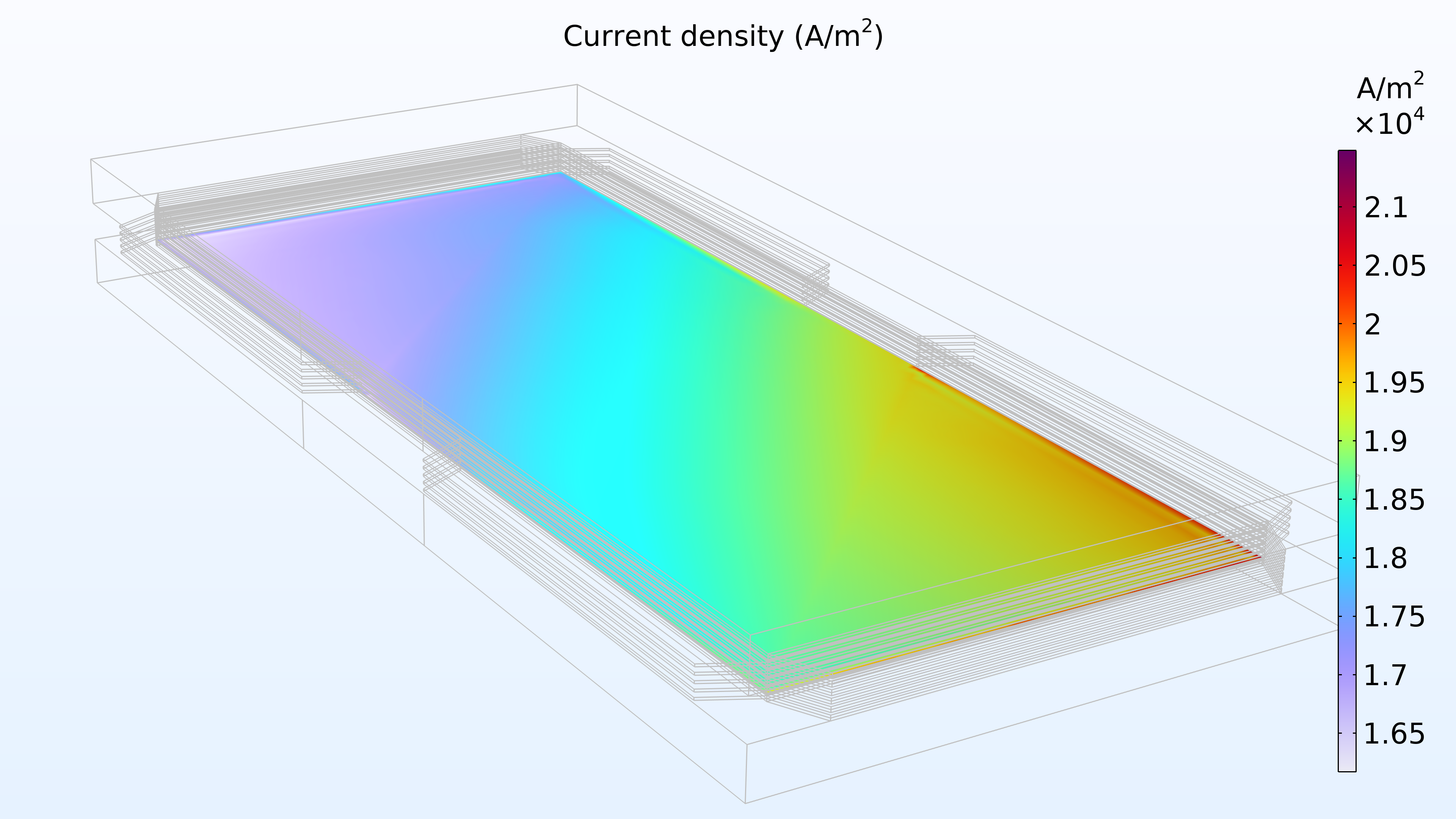
Figure 14 shows the current density distribution in the membrane between the electrodes. The supply of air seems to determine the charge transfer rate, resulting in a higher current density at the air inlet and a low current density at the air outlet. In addition, the current density distribution is almost identical at the top, middle, and bottom of the stack.

Figure 14. Current density between the electrodes in the membrane in the top cell (left), middle cell (middle), and bottom cell (right).

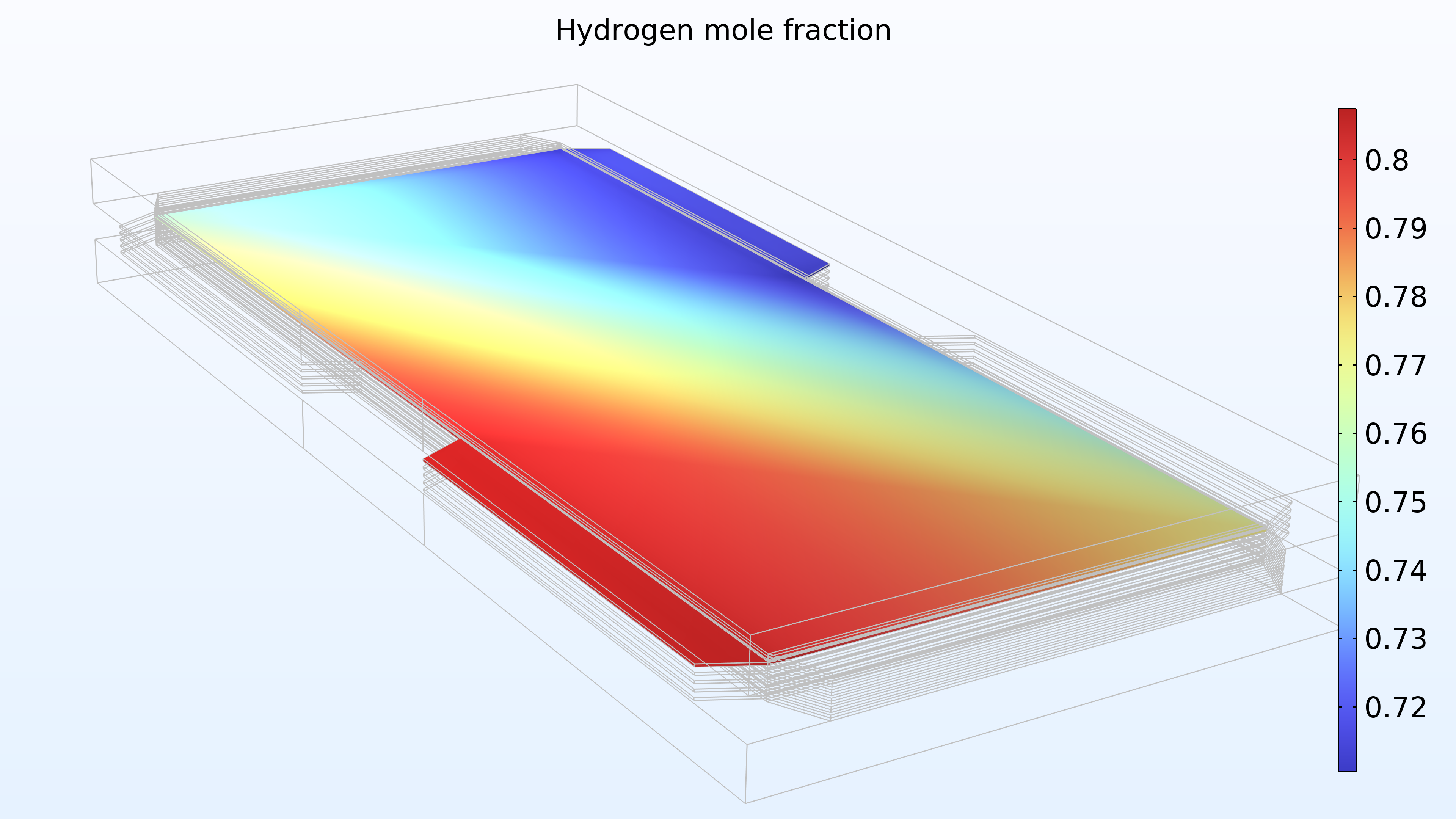
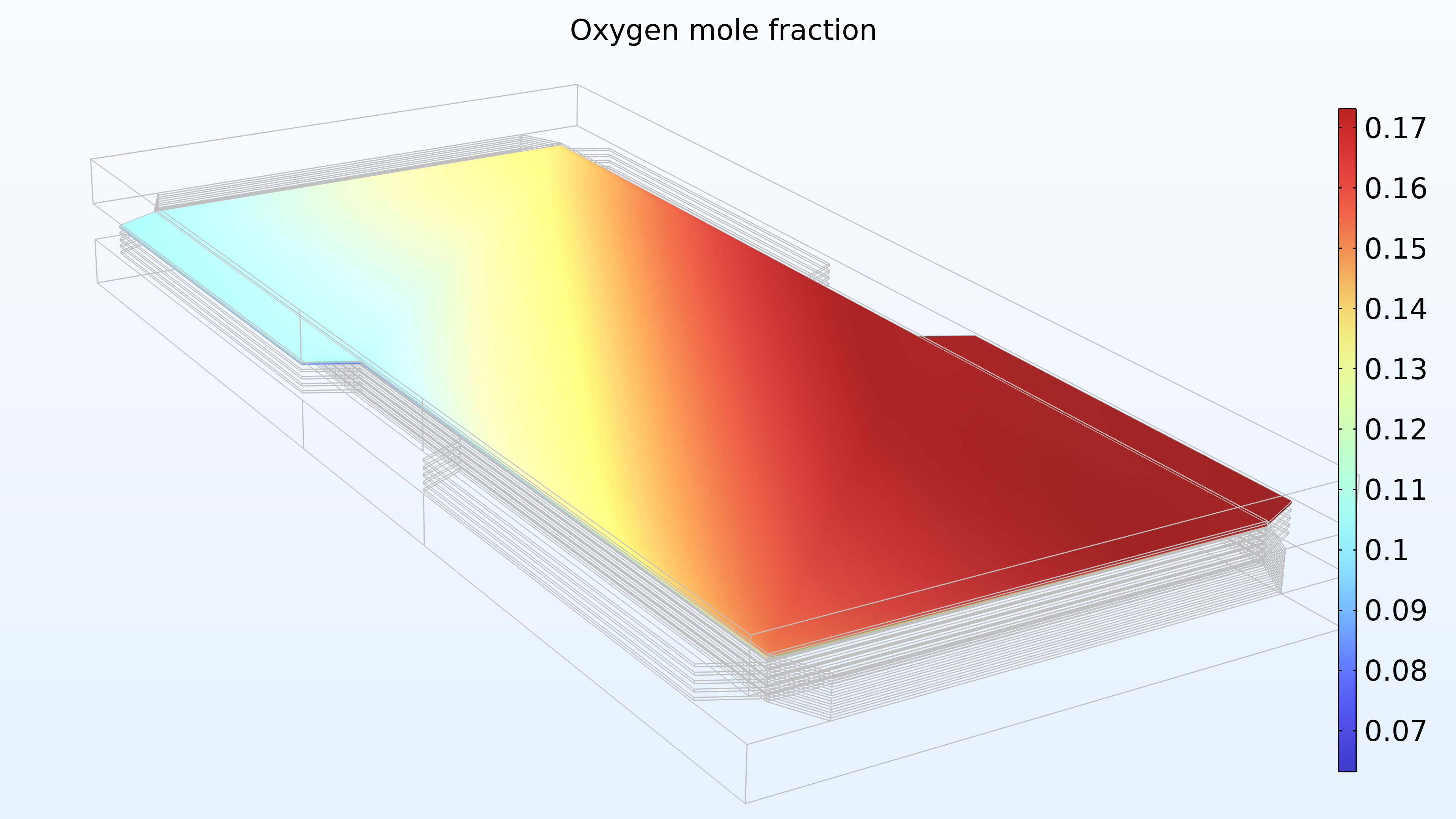
Figure 15 shows the hydrogen and oxygen mole fractions in the top cell in the gas channels and the porous electrodes. As expected, the current density distribution above reflects the profile of the oxygen mole fraction. Note that oxygen is depleted to a much larger extent than hydrogen. In addition, oxygen is depleted along the thickness of the cathode, while the hydrogen mole fraction is almost constant along the thickness of the anode.

Figure 15. Hydrogen mole fraction (left) and oxygen mole fraction (right) in the top cell in the stack.

Figure 16 shows the temperature in the top cell of the stack in the cathode gas channels and electrode, membrane, and anode channels and electrode, represented from right to left in the color legends. The temperature is higher in the membrane, which is expected since the membrane has lower electrical and thermal conductivity. In addition, the temperature increases in the direction of the cooling water, which is also expected.

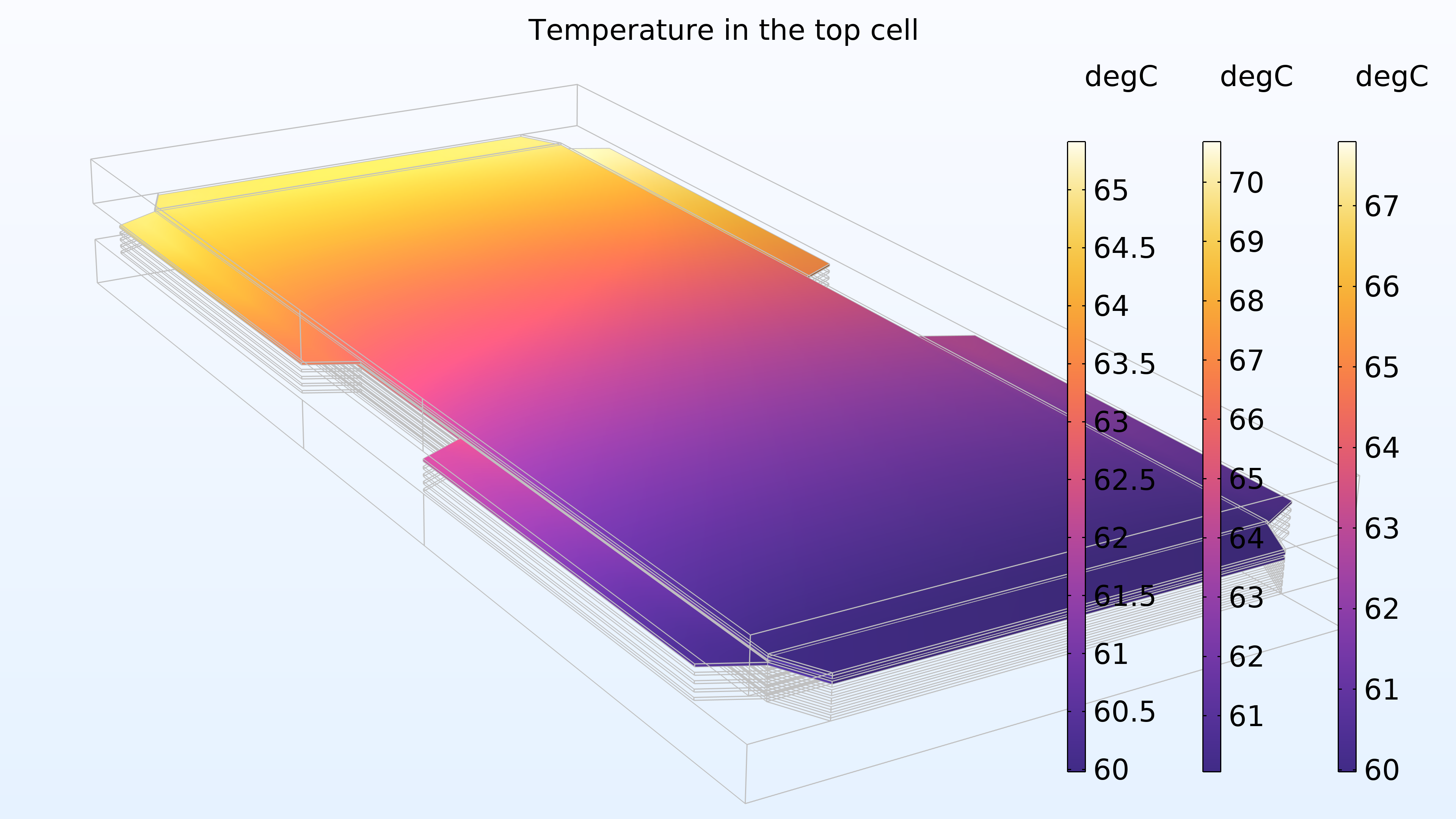
Figure 16. The temperature in the top cell in the stack.

Figure 17 shows the temperature in the stack. The highest temperature is obtained in the membrane of the middle cell. This location is furthest away from the end plates, which contribute with some cooling. The cooling channels in the bipolar plates also provide cooling. In addition, we can see that the temperature distribution is identical in the two end plates.

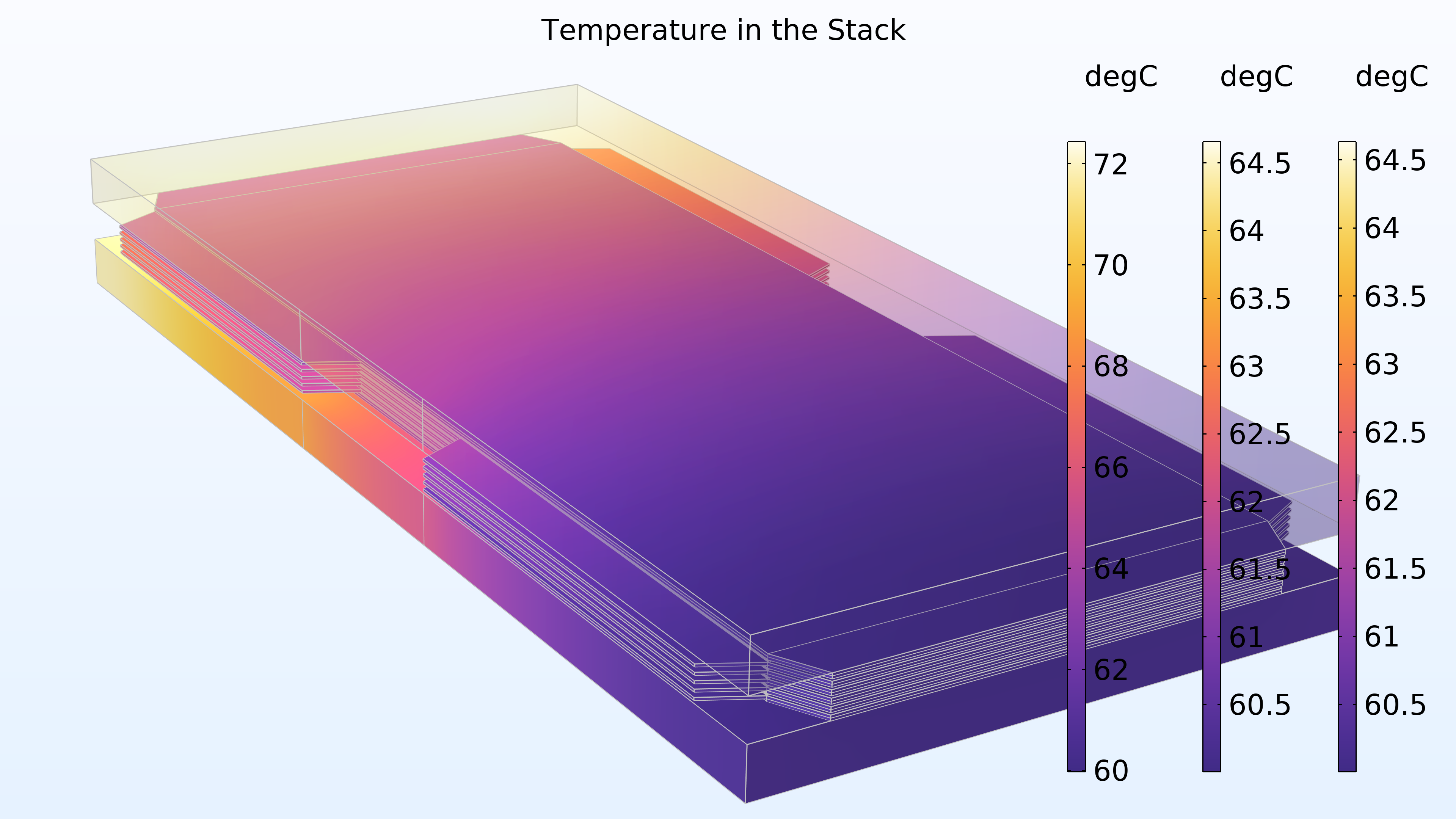
Figure 17. Temperature in the stack. The right and middle color legends correspond to the end plates, while the left color legend corresponds to the cells.

The model shows a slight variation along the height of the stack. This would change if we were to stack more cells, which would result in oxygen or hydrogen depletion along the height of the cells, with variations also in the gas channels in the manifold.

Next Steps

These are just a few examples of how modeling and simulation can be used for fuel cell development, but there are many more. By using simulation to gain a deeper understanding of fuel cells, engineers can continue to advance the overall efficiency, power, and reliability of these cells.

Note that all of the examples shown here would typically be built using the Fuel Cell & Electrolyzer Module. Learn more about this module — which can be used for modeling hydrogen fuel cells, industrial electrolyzers, and much more — by clicking the button below!

Explore the Tutorial Models

Try using the abovementioned tutorial models yourself. Clicking the links below will take you to their Application Gallery entries, where you can download the accompanying MPH-files.

1. Current Density Distribution in a Solid Oxide Fuel Cell
2. Low-Temperature PEM Fuel Cell with Serpentine Flow Field
3. Nonisothermal PEM Fuel Cell
4. Fuel Cell Stack Cooling