Equation-Based Modeling Blog Posts

Solving Delay Differential Equations to Model…Marmots?
As of COMSOL Multiphysics® version 6.3, it’s possible to model delay differential equations. Explore this functionality in the context of a whimsical example.

How Well Do Mosquito Traps Work? Observing Their Effectiveness with Particle Tracing
Are you a mosquito magnet? For fun, let’s explore whether mosquitoes prefer mosquito traps or human skin with equation-based modeling.

Forming New Ideas with Generative Design in COMSOL®
Pencils were invented in the 16th century and erasers in the 18th century. However, it wasn’t until the 19th century that erasers were attached to pencils in the typical design we know today.

Why Do Golf Balls Have Dimples?
Why do golf balls have dimples? Can I model a golf ball with COMSOL Multiphysics? Can I use simulation to optimize my shot and make a par? Find answers to these questions and more…

Micromagnetic Simulation with COMSOL Multiphysics®
A guest blogger from Fudan University in China used the Physics Builder in COMSOL Multiphysics to create a “Micromagnetics Module” for performing micromagnetic simulations.
How to Model Metabolic Reaction Networks with COMSOL®
Certain ice creams, puddings, and candies have an extremely vivid yellow color that comes from vitamin B2. The manufacturing of this supplement is one example of a metabolic reaction network…

Combining Adaptive Mesh Refinement with Data Filtering
In a follow-up to our previous blog post on data filtering, we demonstrate how to implement adaptive mesh refinement and a Helmholtz filter for a thermal model with a nonuniform heat load.
Using Data Filtering to Improve Model Performance
Want to include experimental data in your model as a load or boundary condition, but the data varies over space or time and is noisy? Try implementing data filtering, such as a Helmholtz filter.

Using Global Equations to Introduce Fully Coupled Goal Seeking
Learn how to introduce a goal-seeking equation, combined with a fully coupled approach, to solve a nonlinear model. (Follow-up to an earlier blog post on goal seeking with a segregated solver.)

Introducing Goal Seeking into the Segregated Solver
Did you know that you can adjust a model input to achieve a desired output in your nonlinear problems? The process involves implementing a global equation into the segregated solver.

Equation-Based Modeling with a Space-Time Discretization
In COMSOL Multiphysics®, almost any expression in a computational model can be modified. For example, using a space-time discretization can make optimization problems easy and fast to implement.
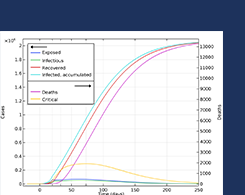
Modeling the Spread of COVID-19 with COMSOL Multiphysics®
From susceptible to exposed and infected to recovered: See how numerical modeling can help us understand the dynamics of the COVID-19 pandemic and how it spreads.
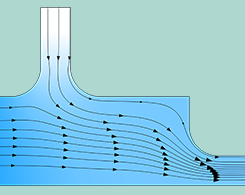
How to Simulate Control Systems Using the PID Controller Add-In
A PID controller can be used in a variety of industries. This blog post demonstrates how a PID controller add-in can be easily incorporated in two simulation examples.

Defeating Giant Movie Monsters Using Mathematical Modeling
The predator-prey equation can predict how we’d fare in a monster invasion, as well as real-world biology and ecology scenarios like shark overpopulation and tumor movement.
Optimizing PID Controller Performance with COMSOL Multiphysics®
PID controllers involve three components that must work together simultaneously, and it can be challenging to get each of them just right. That’s where process control simulation comes in.

Introduction to Numerical Integration and Gauss Points
In this comprehensive blog post, we go over the theory behind numerical integration, Gaussian quadrature, Gauss points, weak contributions, and much more.

Simulation Applications Enable Digitalization at ABB Traction Motors
Here’s a real-world example of optimizing R&D processes with COMSOL Server™: At ABB Traction Motors, engineers use simulation applications to analyze CFD and heat in electric motor designs.

3 Approaches to Modeling Moving Loads and Constraints in COMSOL®
Learn 3 ways to model moving loads and constraints in COMSOL Multiphysics®: using variables, interpolation functions, and paths imported from CAD geometries.

Nonstandard Constraints and the Power of Weak Contributions
For a flexible and physics-independent way to extend the applicability of the COMSOL Multiphysics® software, you can implement nonstandard constraints using the so-called weak contributions.

How to Implement the Weak Form for Time-Dependent Equations
Here’s a comprehensive equation-based modeling guide on how to implement the weak form for time-dependent equations, including theoretical background and step-by-step instructions.

Image Denoising and Other Multidimensional Variational Problems
Learn how to solve variational problems featuring multiple dimensions, higher-order derivatives, and multiple unknowns with a fun example: image denoising in a grainy photograph.

Methods for Enforcing Inequality Constraints
Learn 2 methods for enforcing inequality constraints in your variational problems, the Lagrange Multiplier method and Augmented Lagrangian method, as well as the theory behind them.

Methods for Dealing with Numerical Issues in Constraint Enforcement
This post is helpful if you use equation-based modeling: Learn a variety of different methods for dealing with numerical issues when enforcing constraints in variational problems.

Specifying Boundary Conditions and Constraints in Variational Problems
In part 2 of a blog series on solving variational problems in COMSOL Multiphysics®, we discuss how to specify general boundary conditions and constraints.
