The rotation of the impellers in a mixer or stirred reactor creates ripples on the liquid surface when the agitation is moderate. If the ripples are small in comparison to the height of the fluid in the vessel, the shape and height of the free surface can be explicitly calculated from the velocity field in a separate solution step. The latest version of the Mixer Module in COMSOL Multiphysics includes a Stationary Free Surface feature for such computationally inexpensive calculations.
Free Surface Shape Computations: The Different Approaches
When calculating the shape of a free liquid surface that is in contact with a gas, there are several methods that you can use. Say, for instance, that you have a case in which the deformations are large and topology changes of the free surface occur (i.e., the breaking of waves or the detachment of droplets from the surface). Here, the level set and phase field methods provide good estimates of the free surface shape. Such techniques can be applied to both time-dependent and steady simulations.
A level set simulation that represents the filling of an enclosure. The topological changes are clearly shown, as new edges are created during the simulation.
Let’s now consider a case in which deformations are large but no topology changes occur in the shape of the free surface. In this situation, the arbitrary Lagrangian-Eulerian (ALE) moving mesh method is able to offer very accurate predictions of the shape of the free surface. The ALE method, which can be applied to both time-dependent and steady simulations, is the default method for computing the shape of free surfaces in the Mixer Module.
A rising bubble simulation that uses the ALE method. The simulation stops when the bubble is about to split into two bubbles at the outer radius, as it involves a change in topology where new edges are created.
The level set, phase field, and ALE moving mesh methods are very accurate in predicting the shape of a free surface, provided that a proper mesh resolution is used in the computations. Such accuracy, however, comes at a high cost. And, when only an estimate of the free surface shape is requested, these methods prove to be quite computationally expensive.
In the latest version of the Mixer Module in COMSOL Multiphysics — version 5.2 — you will find a relatively inexpensive method for computing the shape of a free liquid surface for stationary flows. The method is valid for situations in which the deformation of the free surface is small; for example, when only ripples form on the surface. In such cases, an equation that uses the velocity and pressure fields as inputs estimates the shape of the free surface, solving for the surface elevation around an average (see equation (1)).
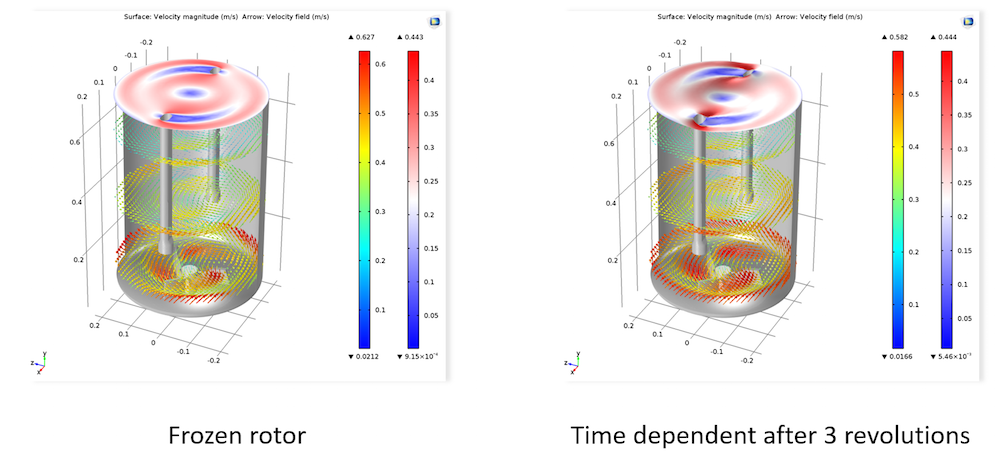
Left: Simulation results for a free surface model in a stationary frozen rotor approximation. Right: Results for a free surface model in a full time-dependent simulation.
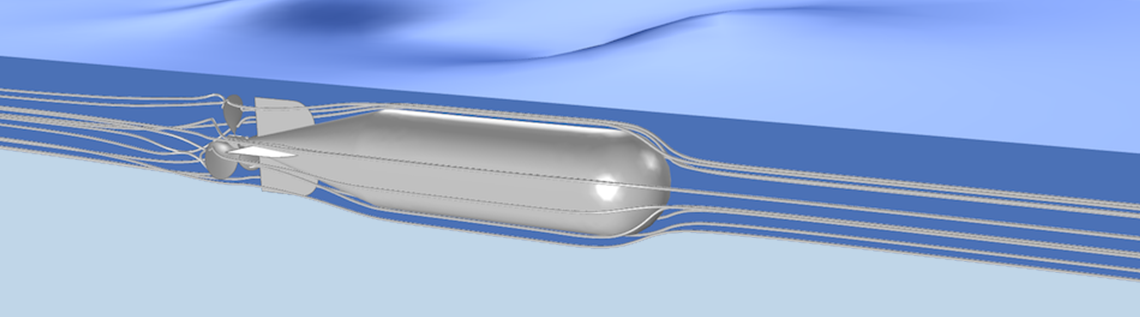
The new functionality is exemplified in the Mixer application that is highlighted in the figures above. It is important to note that the method can also be used to compute the free surface shape of stationary fluid flow problems that involve rotating machinery in general, an application that is illustrated in the figure below.
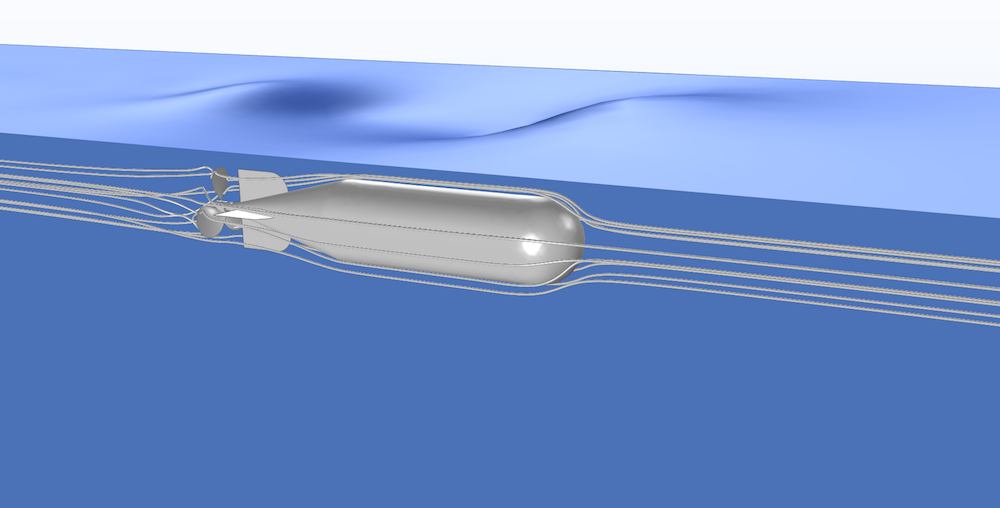
A simulation of a World War II torpedo. The torpedo travels close to the water’s surface, producing ripples.
Next, we’ll take a closer look at the physics behind stationary free surface computations as well as the feature itself.
The Principle Behind Stationary Free Surface Calculations
The deformation of a free surface is calculated from the pressure distribution, p, on the boundary obtained from the flow field solution of the Navier-Stokes equations. When computing the flow field, a slip condition, together with a constant pressure level, {p_{ext}}, is applied on the boundary. The free surface deformation, {\eta }, is evaluated from the linearized free surface condition according to the following equation:
(1)
where {\mathbf{n}} is the surface normal and {{\mathbf{x}} = {{\mathbf{x}}_0}} represents the position of the undisturbed surface. On the right-hand side of the equation, the surface tension coefficient, \sigma, is multiplied by the linearized surface curvature. The equation gives an approximation of the force balance at the free surface, which is valid for small surface deformations and small gradients of the deformations.
Using the Stationary Free Surface Feature
The Stationary Free Surface feature, available in the Rotating Machinery, Fluid Flow interface, provides an easy way for you to estimate the deformation of a free surface as a result of volume and fluid flow forces.
As the screenshot below illustrates, the Mixer Module adds the Stationary Free Surface feature to the model tree. By selecting the feature, you further enable the Stationary Free Surface study step. This study step solves the equation for the surface elevation equation referenced above, utilizing the velocity and pressure field from a previous stationary study step.

The Stationary Free Surface feature with the corresponding study step in the model tree.
As its name suggests, the Stationary Free Surface feature can only be applied to steady flows. (As we mentioned earlier, the level set, phase field, and ALE free surface computation functionalities are all available for time-dependent flow simulations.) A natural step for an extension to this feature is to add similar functionality for time-dependent simulations.
Further Reading
- Download related tutorials from the Application Gallery
- Interested in learning about what else is new in the latest version of COMSOL Multiphysics? Head on over to our 5.2 Release Highlights page




Comments (1)
vinh thiều
January 10, 2019Dear Ed Fontes
I’m Vinh, a senior student in HaNoi University of science and Technology.
i want to simulation a water paint stirring process. Cause my knowledge is not enough, although i try hard to create a model for mixer but so much error appearance. Can you give me some advice about the physics, studies,… which is fit with my project.
Thank you very much.