
Known as the “father of information theory”, Claude Shannon shaped the way we think about computer operations and communications between devices as a single framework. His groundbreaking ideas about testing digital circuits, coding messages in binary, and programming artificial intelligence ushered us into the digital age. The internet was made possible by Shannon’s classical foundations in information science, and thanks to his equations, the amount of data we’re able to store and share consistently increases.
Claude Shannon: From Model Planes to MIT
Claude Shannon was born on April 30, 1916, in Petoskey, Michigan, and spent most of his childhood with his family in Gaylord, Michigan. From a young age, Shannon showed a keen interest in mechanical and electrical engineering, constructing model planes and a radio-controlled boat. He also showed an aptitude for communications technology. Inspired by Thomas Edison’s improvements to the telegraph, Shannon built a telegraph of his own out of barbed wire and connected it from his house to a friend’s house.

Claude Shannon. Image by Jacobs, Konrad. Licensed under CC BY-SA 2.0 DE, via Wikimedia Commons.
After earning bachelor’s degrees in both mathematics and electrical engineering from the University of Michigan, Shannon began his graduate studies in 1936 at the Massachusetts Institute of Technology (MIT). He went on to earn a master’s degree and PhD from MIT. His master’s thesis, written when he was 22 years old, forever changed how we use digital circuits in computing and automation.
Connecting Ideas in Communications Technology
Claude Shannon spent his time at MIT industriously. A summer internship with Bell Laboratories secured a lifelong affiliation with the company and deepened his interest in electrical engineering. He also worked at MIT as a research assistant to acclaimed researcher Vannevar Bush, with whom Shannon designed switching circuits on Bush’s differential analyzer, an early analog computer. He based the design of these circuits on the concepts of mathematician George Boole.
In 1937, Shannon wrote his master’s thesis, “A Symbolic Analysis of Relay and Switching Circuits”. Drawing from his experience with the differential analyzer, he used Boolean algebra to establish the theory behind digital circuitry. This revelation gave engineers the ability to test circuit designs with Boolean algebra before investing time and money into building a prototype. In addition, Shannon was able to prove that Boolean algebra and binary arithmetic could be used to arrange circuits in a simplified way.
A partial view of a two-layer printed circuit board geometry. The file is provided through the courtesy of Hypertherm, Inc., Hanover, NH, USA.
Previously, engineers used ad hoc methods for digital circuit design, but Shannon’s applied theory made more intentional connections with a focus on network synthesis. With Shannon’s simplified arrangements of electromechanical relays, such as those used in telephone switches, electrical switches could perform logic. This ability laid the foundations for the basic functions of a computer.
Cracking the Communications Theory Code
During World War II, Claude Shannon was working at Bell Labs under contract with the National Defense Research Committee (NDRC), where he specialized in fire-control systems and cryptography. As a cryptographer, Shannon used digital codes to protect sensitive information. He realized, as the war was coming to an end, that he could also use digital codes to address a signal noise interference problem he often encountered, and thereby protect messages from such interference. He started thinking about cryptography’s relationship to communications theory and began developing mathematical formulations that explored the nature of the transmission of information.
Introducing Information Theory
Claude Shannon’s work up to this point served as the basis for his landmark 1948 paper, “A Mathematical Theory of Communication”, which introduced information theory as a definitive field. He was able to establish the results for information theory so completely that his framework and terminology are still used today. He was also the first to use the word “bit” to mean a single binary digit. The bit is now also referred to as the shannon (Sh), a unit of information and entropy.
In this paper, Shannon poses two key questions:
- What is the most efficient encoding of a message using a given alphabet in a noiseless environment?
- What additional steps should be taken when noise is present?
To answer these questions, Shannon came up with a way to efficiently transmit messages and measure the efficiency of transmissions. All messages, he purported — whether conveyed via telephone, television, or radio — might be delivered inaccurately due to the presence of noise. The aim, then, is to find a way around the noise. He suggested that a message should be constructed as a sequence with statistical properties — in other words, in bits, or binary digits (ones and zeros). In this way, the message’s coding can be minimized and transmitted more effectively, regardless of the presence of noise, and then easily reconstructed and interpreted by a recipient device.
As a way to measure the efficiency of a communications system, Shannon developed information entropy. The higher the entropy of the message, the more effort it takes to transmit it.
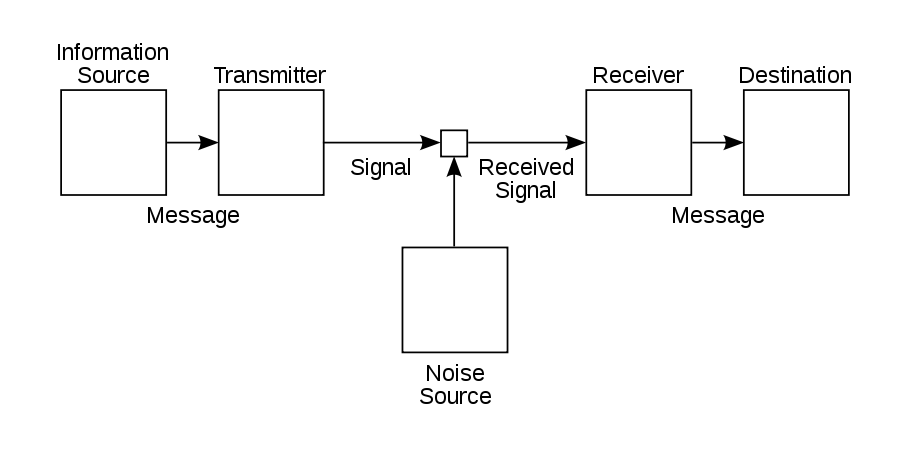
A schematic of Shannon’s communication system from his 1948 paper. Image in the public domain, via Wikimedia Commons.
Furthermore, Shannon was able to show that bandwidth and noise are factors characterizing any communications channel, and the maximum rate at which data can be transmitted with zero error for a given channel can be calculated. This is known as Shannon’s channel capacity, or Shannon’s limit.
In subsequent articles on information theory, Shannon introduced sampling theory. Sampling converts a signal into a numeric sequence, and sampling theory bridges continuous time signals (analog signals) and discrete time signals (digital signals). Shannon’s version of the theorem proved a dual of fellow engineer Harry Nyquist’s results. The Nyquist-Shannon sampling theorem, often used in wave optics studies, honors the scientists for this reason.
Theseus, the A-MAZE-ing Automated Mouse
It’s obvious that Claude Shannon worked hard — but he had a reputation for playing hard as well. He was known for taking rides through the halls of Bell Laboratories and MIT on a unicycle (while juggling four balls, no less). In his home near Boston, which he dubbed “Entropy House”, he displayed a framed paper certifying him as a “doctor of juggling” among his legitimate diplomas and awards.
One of his inventions stands above the rest as a step toward artificial intelligence: “Theseus” or Shannon’s mouse. Theseus is a magnetic mouse controlled by an electromechanical relay circuit that allows it to move around a special maze with 25 squares. Each of the partitions can be moved around to reconfigure the maze, and the mouse’s “goal” is to go through the maze until it reaches a prize.

Theseus and its maze at an MIT Museum exhibit. Image by Daderot. Image in the public domain, via Wikimedia Commons.
The genius of Shannon’s design shows in the mouse’s programming: Once the mouse goes through the maze, it can be picked up and put back inside the maze anywhere it has already been and find its way to the prize based on its prior knowledge. If Theseus is placed in an unfamiliar location within the maze, it finds its way to a known location. Once reaching familiar territory, Theseus resumes its prime mission of finding the target. The Theseus experiment set a precedent for the machine learning systems we’re familiar with today.
Besides riding a unicycle and programming a magnetic mouse, Shannon was always tinkering with computer machinery and automation, as the following list of his inventions proves:
- Computerized chess
- Automated pogo stick
- Rocket-powered frisbee
- “Mind-reading” machine built out of mechanical relays that could predict a player’s behavior
- THrifty ROman numeral BAckwards-looking Computer (THROBAC), which calculates in Roman numerals
- “Ultimate” or “Useless” machine, in which you flip a switch to turn it on and mechanical hand pops out of the box to turn it off again (Watch a video to see it in action!)
- Device that solves the Rubik’s Cube® puzzle
Celebrating Shannon and the Digital Revolution
Claude Shannon is widely celebrated for his many contributions to the field of computing. His master’s thesis is considered one of the most important of the 20th century and won Shannon the Alfred Noble American Institute of American Engineers Award. While the Nobel Prize is not offered in his specific field, he won the Kyoto Prize, Japan’s equivalent award. He was also awarded the IEEE Medal of Honor. On his centenary in 2016, the IEEE Information Theory Society coordinated worldwide events and activities in his honor.
Shannon was truly ahead of his time in 1948. While his revolutionary information theory was not seen as immediately applicable, we now see its influence in every device containing a microprocessor or microcontroller. He established the parameters for compressing and transmitting digital information, which enables you to access and read this COMSOL Blog post — perhaps even from your mobile device.
Let’s wish Claude Shannon a happy birthday!
Further Reading
- Learn more about Claude Shannon:
- Read about these other scientists:
Rubik’s Cube is a registered trademark of Rubik’s Brand Ltd. Corporation.






Comments (0)