
From the development of the coaxial cable and the modern Maxwell’s equations to the discovery of the Kennelly–Heaviside layer, we have Oliver Heaviside to thank. Heaviside was a self-taught mathematician and physicist who spent much of his life studying in solitude, dedicated to his books. His story shows that some of the most impactful inventions and ideas come from curiosity, self-discipline, and isolation…
Early Life
A Close Tie with a World-Famous Writer
Oliver Heaviside, the youngest of Thomas Heaviside and Rachel Elizabeth West’s four sons, was born on May 18, 1850. His father was a wood engraver and watercolorist, and his mother was a teacher for neighborhood children. Throughout his childhood, Heaviside and his family lived in Camden Town, London, in a home located around the corner from where one of the most influential writers of the 19th century once lived: Charles Dickens. Like Dickens, Heaviside also grew up on the edge of poverty.
At the time, cases of scarlet fever were on the rise throughout the world, with several severe epidemics occurring in North America and Europe. Unfortunately, this epidemic impacted Heaviside’s life in a major way. After catching this bacterial infection when he was a young child, Heaviside was left with a permanent hearing impairment, which, he said, made it very difficult for him to connect with his peers.

A photograph of Oliver Heaviside, taken around 1900. Image in the public domain, via Wikimedia Commons.
Despite his hardships, Heaviside excelled in grammar school, once placing fifth on a College of Preceptors examination administered to more than 500 students. However, with printing technology rapidly evolving, competing with his father’s engraving work, Heaviside’s family could no longer afford to keep him in school. At the age of 16, Heaviside’s education, in the formal sense, came to an end.
A Brief Career as a Telegrapher
Heaviside’s luck began to turn around when his uncle Charles Wheatstone, an English physicist who popularized the use of the Wheatstone bridge and coinvented an early version of the telegraph, took an interest in furthering his nephew’s education and career. In 1867, Wheatstone offered Heaviside a position to work at one of his telegraph companies in Newcastle upon Tyne, a city in northeastern England. Heaviside accepted his uncle’s offer. Here, Heaviside worked alongside his older brother, Arthur, who Wheatstone had hired to help manage the company. Two years later, in 1869, Heaviside accepted a role as a telegraph operator at the Great Northern Telegraph Company in Denmark. After three years, Heaviside moved back to Newcastle upon Tyne, where he handled overseas communication for the same company.
A sketch of Charles Wheatstone. Image in the public domain, via Wikimedia Commons.
In 1873, Heaviside learned of James Clerk Maxwell‘s Treatise on Electricity and Magnetism; he became so enthralled by the work that he opted to study it full time, leaving his role as a telegrapher in the process. Although Heaviside would not be employed again in the traditional sense, he stayed busy with his studies. Ultimately, this decision led him to make countless groundbreaking findings in the fields of electrical engineering, mathematics, and physics, within a small, spare room in his parents’ home.
The Many Discoveries of Heaviside
Inventing the Coaxial Cable
After just a few years of researching at home, Heaviside invented and patented the first coaxial cable, a type of self-shielded electrical cable. The idea for the invention stemmed from his studies on telegraph lines. In his patent, Heaviside wrote:
“When a number of wires run parallel to one another, either suspended or otherwise, any change in the current flowing in one wire causes currents in all the rest by induction, and the effect may be so great as to seriously interfere with the working of telephonic circuits, and to a less degree of ordinary telegraphic circuits also.”
Farther into the patent, Heaviside describes how the design of his coaxial cable provides a solution to this issue. He said that the design of a coaxial cable:
“…use two insulated conductors for the circuit, and place one of them inside the other; thus, one conductor may be a wire, and the other a tube or sheath, which must also be insulated. When the tube and inner wire are electrically connected at both ends of the line, as through apparatus in the usual manner, the circuit as thus described is completely independent of other circuits, and any number of such circuits, each containing an insulated tube and inner wire, may be laid side by side without any mutual inductive interference, and without interference from other wires worked in ordinary manners.”
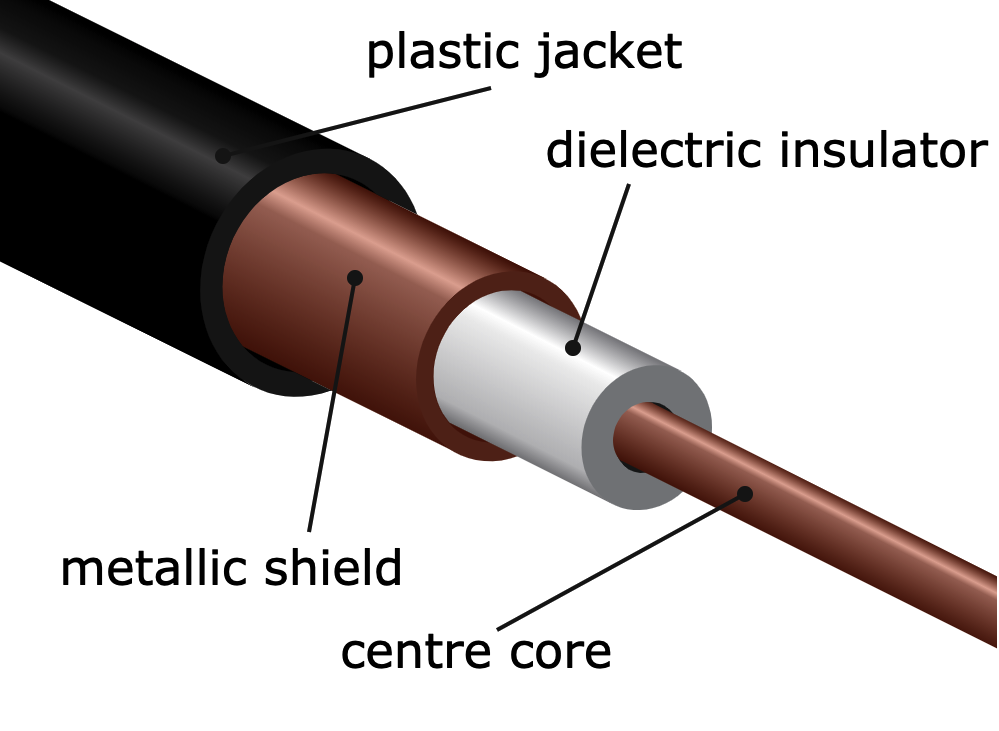
A schematic of a coaxial cable. Image licensed under CC BY 3.0, via Wikimedia Commons.
Recasting Maxwell’s Equations
In 1884, still fascinated by James Clerk Maxwell’s Treatise, Heaviside made one of his more memorable accomplishments. While studying the book, he became especially interested in Maxwell’s equations, a set of equations that describe the behavior of electric and magnetic fields and how they interact with each other. However, these equations were difficult to understand and slow to be accepted, as they were published in a set of 20 equations in 20 different variables. After an in-depth analysis of these equations, Heaviside was able to reduce the cumbersome form of them down to four vector equations, which is the form in which they are most often taught in today. Below, you can see Maxwell’s equations listed in their differential form:
\begin{align*}
\begin{split}
\nabla \cdot \textbf{D} = \rho, \quad \text{(Gauss’ law)} \\
\nabla \times \textbf{E} = -\frac{\partial\textbf{B}}{\partial t} , \quad
\text{(Faraday’s law)} \\
\nabla \cdot \textbf{B} = 0, \quad \text{(Magnetic Gauss’ law)} \\
\nabla \times \textbf{H} = \textbf{J} + \frac{\partial\textbf{D}}{\partial t} , \quad
\text{(Maxwell{-}Amp\`{e}re’s law)} \\
\end{split}
\end{align*}
\end{equation}
Creating the Telegrapher’s Equations
The following year, Heaviside went on to make yet another impactful discovery: the telegrapher’s equations, which, as defined on their Wikipedia page, “are a pair of coupled, linear partial differential equations that describe the voltage and current on an electrical transmission line with distance and time.”
While developing the telegrapher’s equations, Heaviside also proposed a solution to enhance the efficiency of transmission lines by reducing their distortion by increasing their inductance. His simple, but accurate, solution was to install inductors at precise intervals along telegraph lines. Although not implemented (or patented) at the time of its discovery, due to the large amount of resources needed to complete such a project, engineers at AT&T adopted the idea in 1897 and developed it into a working design.
The Kennelly–Heaviside Layer
In 1902, at age 52, Heaviside became interested in the workings of electromagnetic radiation, specifically radio wave propagation (a popular topic in the science community at the time). Simultaneously, Heaviside and U.S. electrical engineer Arthur Kennelly came to the conclusion that “…radio waves propagated around the world because they bounced off a layer of charged gas particles in the ionosphere”, according to this Nature article. The existence of this layer was experimentally proven over 20 years later, in 1924, by English physicist Edward Victor Appleton, who eventually won a Nobel Prize in Physics for his work.
Today, this ionospheric layer, which occurs between 90 km and 150 km (56 and 93 mi) above the ground, is often called the Heaviside layer, Kennelly–Heaviside layer, and the E region. Thanks to this region, long-distance radio communication is possible.
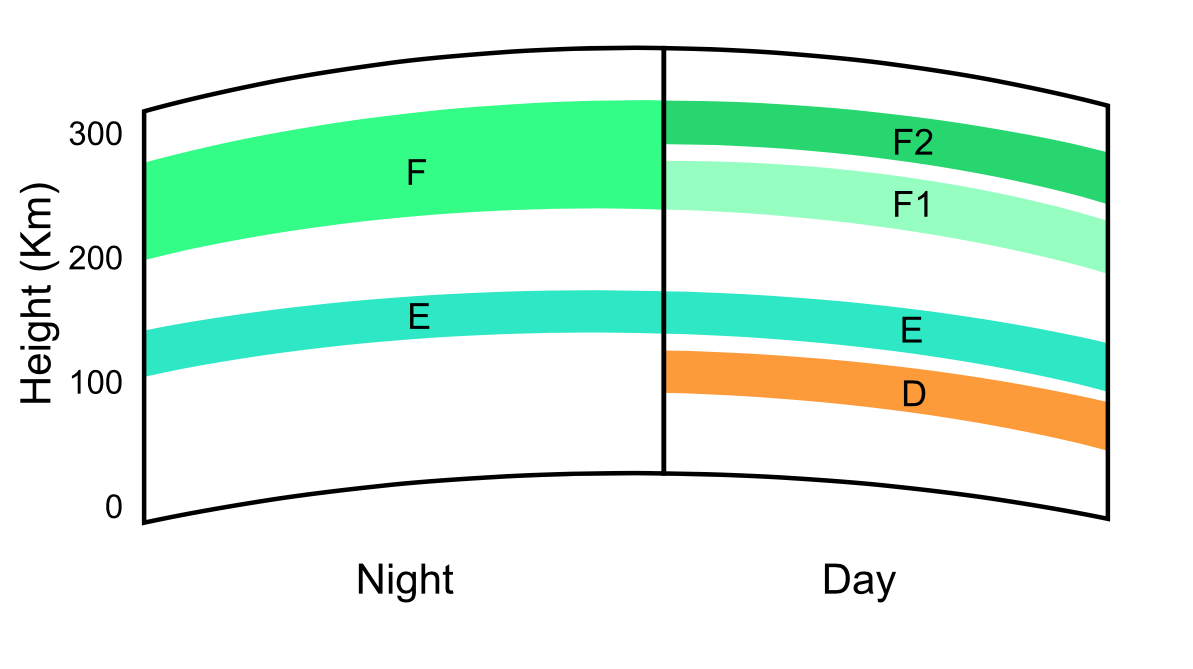
A schematic of the ionospheric layers. (Fun fact: The ionosphere plays a role in enabling certain spiders to float in the sky for hundred of miles.) Photo by the Naval Postgraduate School, licensed under CC BY-SA 3.0, via Wikimedia Commons.
If you are a musical buff, you may be familiar with the phrase: “Up up up past the Russell hotel / Up up up to the Heaviside layer”. This famous line from Andrew Lloyd Weber’s musical Cats pays tribute to the Heaviside layer, bringing science and the arts together.
Other Works
In addition to all of his abovementioned work, Heaviside also coined a variety of terms in electromagnetic theory, including, but not limited to, admittance, conductance, impedance, inductance, permeability, permittance, and relecutance. He also made a countless number of contributions to the field of mathematics, which is why his name appears frequently in a variety of methods, functions, and conditions, including:
- Heaviside cover-up method
- Heaviside step function
- Heaviside condition
- Heaviside–Feynman formula
Lasting Legacy
Despite leaving school in his youth, Heaviside’s accomplishments and self-studies earned him an honorary doctorate from the University of Göttingen in 1905. Then, in 1922, Heaviside was the first recipient of the Faraday Medal, one of the most prestigious awards for engineers, inventors, and scientists, named after physicist and chemist Michael Faraday. At the age of 74, Heaviside passed away on February 3, 1925, while living in Devonshire.


The front (left) and back (right) of the Faraday Medal. The image on the left is licensed under CC BY-SA 4.0, via Wikimedia Commons, and the image on the right is licensed under CC BY-SA 4.0, via Wikimedia Commons.
Recently, in honor of the life and work of Oliver Heaviside, English Heritage, a charity in charge of over 400 historic buildings, documents, and places, added a blue plaque near the location of Heaviside’s childhood home. In an article on English Heritage’s website, Howard Spencer, a senior historian at English Heritage, said: “Oliver Heaviside was a physicist whose theories framed one of the biggest recent technological leaps of humankind — the development and advancement of electrical communications. Both the mobile phone in your pocket and the old-school landline at home owe plenty to Heaviside’s work.”
Today, let’s wish Oliver Heaviside a happy birthday!
Further Reading
- Learn more about the life and work of Oliver Heaviside here:
- Read about the work of related engineers and scientists on the COMSOL Blog:



Comments (0)