
In electromagnetics simulations, the ultimate goal is to boost the efficiency and productivity of your device by closely mimicking the effects observed in reality. This process requires an understanding of the reality you are trying to describe and mimic, as well as the details that should be included. Let’s explore the reality of electromagnetic waves with regards to the measurement environment.
Measuring Electromagnetic Waves in the Real World
When characterizing electronic devices radiating electromagnetic waves, it is important to make sure that the radiated waves are not returning to the device under test (DUT). Infinite space without surrounding objects is ideal. Such an environment hides effects from reflection (i.e., multipath fading) that will cause a phase distortion when the reflected waves are added to the original wave. The closest equivalent to this setting on Earth is an open field, though there is still a significant effect from the ground.

An antenna in the middle of an open field. Image by Dr Patty McAlpin. Licensed under CC BY-SA 2.0, via Wikimedia Commons.
If we know the exact spatial configuration between a transmitter and a receiver and are sure that the ground is the only object distorting the waves, we can remove the unwanted signal path using a time-gating feature with a network analyzer. It is, however, not ideal to have to haul heavy equipment over to the open field every time you need to take measurements. Instead, it would be more convenient if you had access to a lab providing effectively infinite space — that is, an anechoic chamber. The anechoic chamber wall absorbs incident waves and does not interfere with the DUT.

Antenna measurement in an anechoic chamber. Image by Max Alexander / PromoMadrid. Licensed under CC BY-SA 2.0, via Wikimedia Commons.
Modeling an Anechoic Chamber
In an earlier blog post, we demonstrated how to design microwave absorbers using COMSOL Multiphysics and the RF Module. The pyramidal shape of periodic lossy structures gradually attenuates incident waves and generates almost no reflection, making the chamber an interference-free environment.
So, can we use these absorbers to simulate an antenna in the anechoic chamber? Of course!
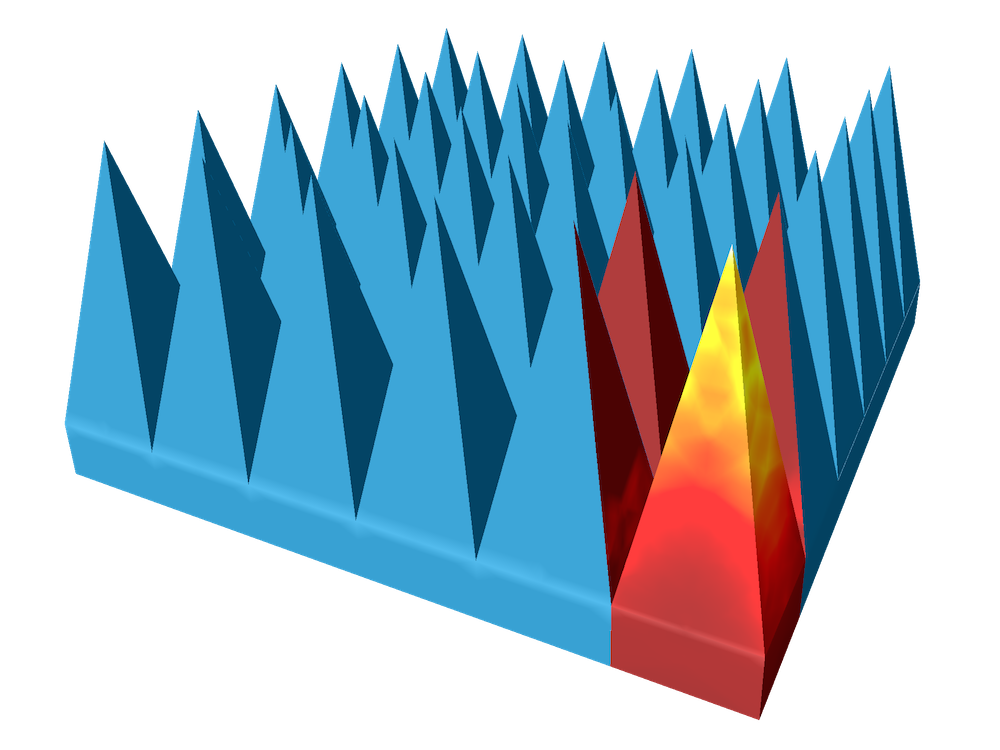
A conventional microwave absorber used in an anechoic chamber.
The geometry of the original pyramidal object is extended to adjust the operating frequency of the absorber for its use with a biconical antenna tuned for the UHF band. The size of the pyramidal object is proportional to the wavelength of interest for the measurement.
The steps for building a model of an anechoic chamber are much like those for building a real-life chamber. We begin by creating an empty room that is 3.9 meters by 3.9 meters by 3.2 meters. The outer wall is covered by a perfect electric conductor mimicking a conductive coating that is thick enough to block all incoming signals from outside the chamber. Absorbers are added on six sides of the walls.
At the center of the chamber, we place our tutorial model of a biconical antenna. Our findings show that the antenna’s performance is very similar to the results found in the example from our Application Gallery. The figure below offers a beautiful visualization of the contours of the magnitude of the electric field.
![]()
Simulation of a biconical antenna in an anechoic chamber.
Due to the chamber’s complicated geometry and size, this simulation requires more than 16 GB of memory. As we will demonstrate next, there is a way to simplify this process.
A More Efficient Modeling Approach
My colleague Walter Frei previously highlighted different approaches for modeling a domain with open boundaries — in particular, perfectly matched layers and scattering boundary conditions. Using perfectly matched layers (PMLs), we can create the perfect anechoic chamber within the simulation environment.
![]()
The frames of a biconical antenna are modeled as boundaries. The surrounding air domain and perfectly matched layers are required for the simulation. Only half of the PMLs are shown in this figure.
For this example, the operating frequency is in the conventional VHF range, which extends from 60 MHz to 240 MHz. To simplify modeling steps and reduce the required computational resources, we assume that the antenna frame structure is geometrically flat and very thin. Because the thickness is greater than the skin depth in the given frequency range, it is reasonable to model the structure as a perfect electric conductor.
A lumped port with a 50 Ω reference impedance is assigned to the gap located at the center of the two structures composed of hexagonal frames. The antenna is enclosed by a spherical air domain. The outermost layers of the air domain are configured as PMLs that absorb all outgoing radiation from the antenna and work as an anechoic chamber during the simulation.
![]()
Electric field distribution on the yz-plane in dB at 70 MHz. The electric field is resonant over the entire antenna structure.
![]()
Voltage standing wave ratio (VSWR) plot with a log scale on the y-axis. It presents a VSWR of approximately 3:1 on average.
The figure above illustrates the electric field distribution in dB, as well as an arrow plot depicting the directional properties of the field at 70 MHz. When the frequency is in the lower range, the electric field is confined to the entire structure. As the frequency increases, the reacting area gradually decreases. Thus, the part of the antenna structure that is responsive to electromagnetic waves becomes shorter around the center of the lumped port. The computed VSWR is approximately 3:1 on average. This is close to the performance of commercial off-the-shelf products of biconical antennas for EMI/EMC measurements.
![]()
3D far-field pattern at 70 MHz. The pattern resembles that of a typical half-wave dipole antenna.
The 3D far-field radiation pattern shows the same omnidirectional characteristics on the H-plane. The suggested modeling configuration requires less than 2 GB of memory to compute the far-field radiation pattern and the VSWR of a biconical antenna made of lightweight hexagonal frames. Thus, it is much easier and faster to set up this model than the full anechoic chamber simulation.
Additional Electromagnetics Simulation Resources
- Check out these related blog posts:
- Download these tutorial models from our Application Gallery:



Comments (0)