Previously on the blog, we discussed why surfaces are sites of special chemical interest and discussed the theories used to describe reactions at surfaces, including when those surfaces are described within homogenized models of porous media. In this blog post, we’ll discuss how chemicals behave when they become attached to a surface by adsorption. Adsorption plays an essential role in many catalytic and sensing processes, so let’s consider how it can be built into your chemical models.
What Is Adsorption?
Sometimes, chemicals stick to surfaces. This can happen at solid surfaces in the gas phase as well as solid surfaces immersed in a liquid solution. The ability to localize chemicals at surfaces can be of interest in sensing and separation processes, as well as a means of catalyzing a chemical reaction. In the first blog post in this series, we discussed why surfaces can often have unique chemistry.
The process of sticking to surfaces is called adsorption. This should not be confused with the word absorption, which refers to a chemical being taken up into the bulk of a solid or solution.
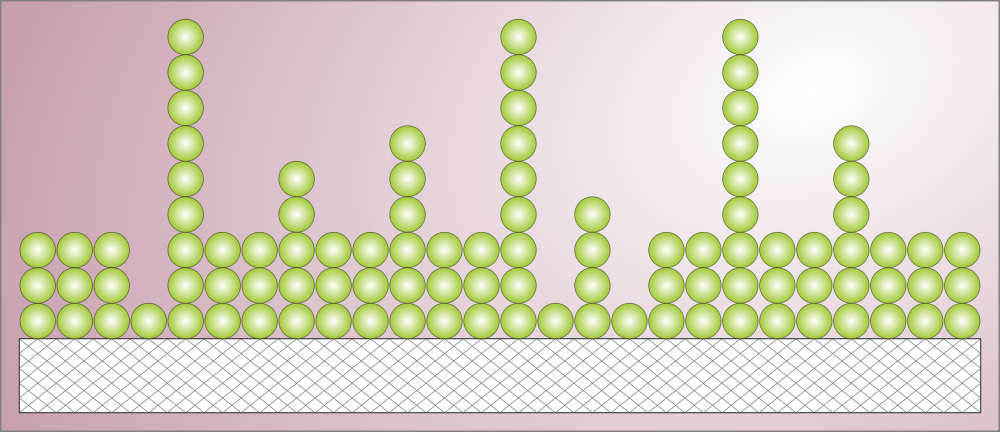
Schematic of BET multilayer adsorption, a type of adsorption. Image by Life of Riley — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
Adsorption may involve a direct chemical bond forming between the surface and the adsorbate (chemisorption) or may involve an attraction between the surface and the adsorbate through intermolecular forces such as hydrogen bonding or van der Waals forces (physisorption). In general, physisorbed molecules are more mobile in the plane of the surface and are adsorbed more weakly.
Adsorption Isotherms
The process of adsorption can be described as an equilibrium reaction:
{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} A(ads)\]
where the chemical species A(g) in the gas phase is called an adsorbate: It becomes adsorbed with a certain rate of adsorption, and then desorbs with a certain rate of desorption.
How do we describe this equilibrium reaction mathematically? One of the simplest approaches is due to the American physical chemist Irving Langmuir. In his model, he proposed the following assumptions:
- There is a maximum surface concentration of adsorbate, csat (mol m-2), at which the surface becomes saturated
- Adsorption rate constants do not depend on the partial coverage of adsorbate: That is, all adsorption sites are identical and mutually independent
- Adsorption is a second-order process whose rate is linear in the adsorbate concentration in the bulk phase adjacent to the surface, as well as the proportion of vacant sites
- Desorption is a first-order process whose rate is linear in the partial coverage of adsorbate
Using these assumptions, we can express the flux of material onto the surface due to adsorption as follows:
where Nads is the flux onto the surface (mol m-2 s-1); kads is the adsorption rate constant (m3 mol-1 s-1); cA is the concentration at the surface in the adjacent bulk phase (mol m-3); and θ is the partial coverage of adsorbate, = cA,ads/csat (unitless), such that (1-θ) is the proportion of vacant sites.
Similarly, the flux of material off the surface due to desorption is:
where kdes is the desorption rate constant (s-1).
At equilibrium, the surface coverage of adsorbate is constant, so the fluxes onto and off the surface must be equal. Equating the expressions above and canceling common terms, we find:
The ratio (kads / kdes) is the equilibrium constant for adsorption and is usually denoted with a capital letter as Kads. The larger this equilibrium constant, the greater the thermodynamic driving force for adsorption. Then, by rearranging the expression above, we can express the fractional surface coverage as:
This is the Langmuir isotherm. For a given temperature, at which Kads takes a certain value, we can predict the fractional surface coverage of adsorbate at equilibrium as a function of its bulk concentration.
Of course, Langmuir’s model is a simple approximation. In real systems, it’s often the case that there are interactions between neighboring adsorbed molecules, so that as the fractional surface coverage increases, it becomes either easier or more difficult to adsorb additional material. Hence, more complicated mathematical models have been developed to account more precisely for real adsorption systems. In particular, the Freundlich isotherm contains an additional empirical constant that can account for interactions between the adsorbed molecules. The BET isotherm can be used for systems in which multilayer adsorption takes place, so that second and subsequent layers of adsorbed molecules are bound to molecules of the same type, rather than the underlying surface of the chemical substrate.
Defining Adsorption in the COMSOL Multiphysics® Software
When setting up chemical species transport and reaction models with the COMSOL Multiphysics® software, you can use a range of tools to introduce adsorption effects in your models.
For adsorption in homogenized porous media, a special Adsorption subnode is available for the Porous Media Transport Properties and Partially Saturated Porous Media domain features. In this subnode, you can define “Langmuir”, “Freundlich”, or “User defined” adsorption for any of the bulk species. Here, we assume that the adsorbed species are at thermodynamic equilibrium with the bulk, so the isotherm relations hold exactly. See the screen capture below for an example of how this Adsorption subnode can be used:
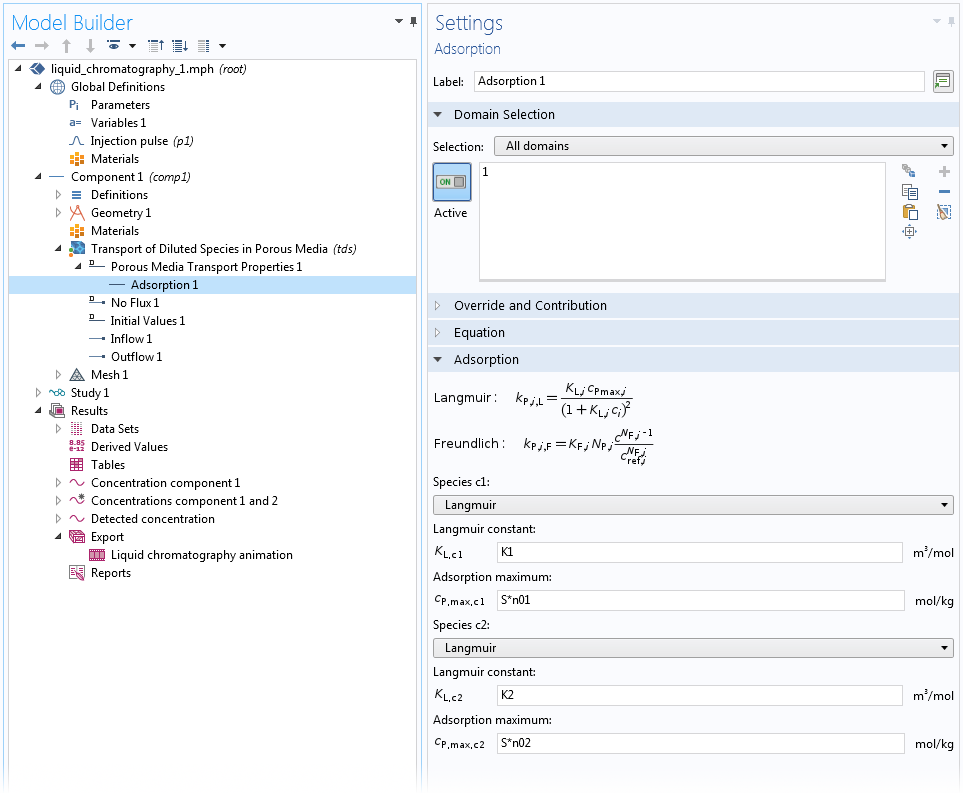
Settings for adsorption of two species on a homogeneous medium in a model of a high-performance liquid chromatography (HPLC) system, using the Langmuir isotherm.
If the adsorption or desorption process is kinetically limited so that the finite rate constants become important and the surface does not remain at equilibrium, then a little more detail is involved in the setup. It’s necessary to use an additional interface to describe the surface concentrations of adsorbed species. As discussed in the first blog post in this series, you can use the Surface Reactions interface to describe adsorbed species. Or, if you are describing a surface distributed through a porous medium, use Transport of Diluted Species with the diffusion coefficient and convective velocity field set to zero.
Adsorption processes represent fluxes that move species from the bulk (gas or liquid solution) phase onto the surface. By adding such a Flux at a boundary or Reactions in a homogenized domain, you can express the adsorption reaction shown above. The kinetics and thermodynamics of this reaction could be set to follow a Langmuir isotherm or one of the more complicated reaction mechanisms, including any user-defined kinetic expression. Remember that typing (ads) directly after the species name allows you to build adsorbed species into the reaction mechanism defined in a Reaction Engineering or Chemistry interface, too.
Another reason for using your own chemical reaction equations to describe adsorption is the case of competitive adsorption, in which two or more adsorbate species share the same adsorption sites. This phenomenon is a common cause of catalyst poisoning: a catalyst becomes inaccessible to its intended substrate due to the stronger adsorption of another molecule. This may result in permanent deactivation of the catalyst for the desired reaction.
Model Examples Involving Adsorption
In the COMSOL Multiphysics Application Libraries, you can find a range of tutorial models that demonstrate different types of adsorption modeling.
Liquid Chromatography
A high-performance liquid chromatography (HPLC) system is modeled in 1D, where the modeled dimension represents progress along the mobile phase in a column. Here, the differing adsorption equilibria, as represented by the Langmuir equilibrium constants for two different components, cause a different degree of retention. The different adsorbed components are separated in space and time due to the combination of a steady flow of solvent and different rates of adsorption.
Here, the Transport of Diluted Species in Porous Media interface is used with the Adsorption subnode to express the equilibrium adsorption processes.
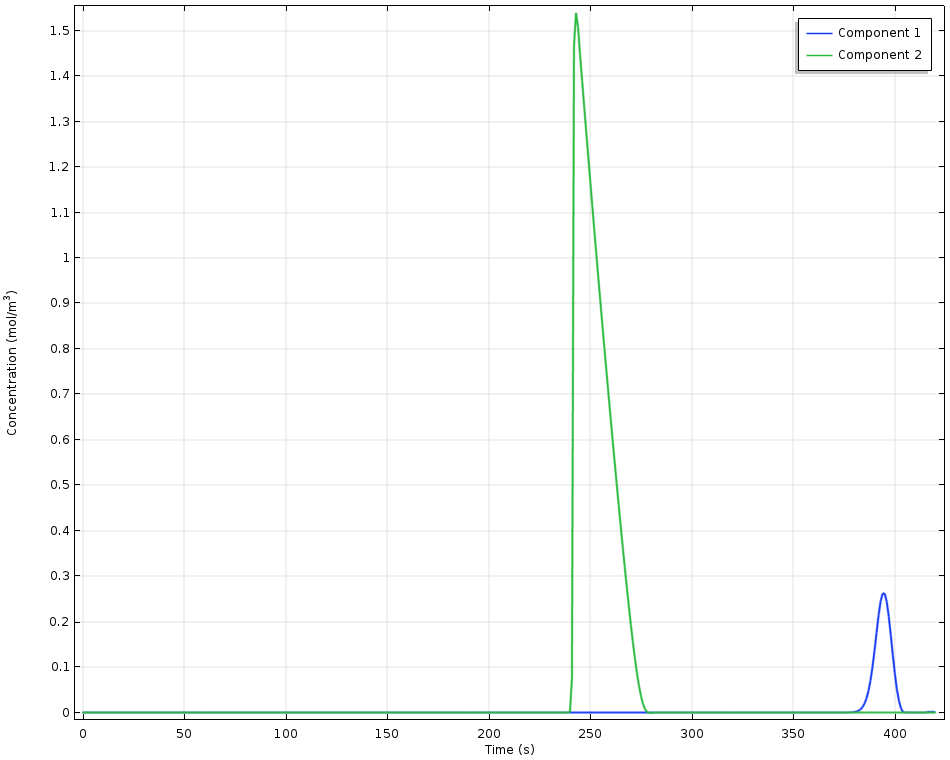
Detected concentrations as a function of time in a high-performance liquid chromatography experiment. Component 1 has higher adsorption capacity and so is retained for longer.
Protein Adsorption
In an ion exchange column, proteins adsorb at sites on the column surface and displace ions, as discussed in this previous blog post on the protein adsorption process. The more complicated reaction mechanism for multiple interacting proteins can be described using the Chemistry interface, which is then coupled to Transport of Diluted Species (for species that are mobile in solution) and Surface Reactions (for adsorbed species).
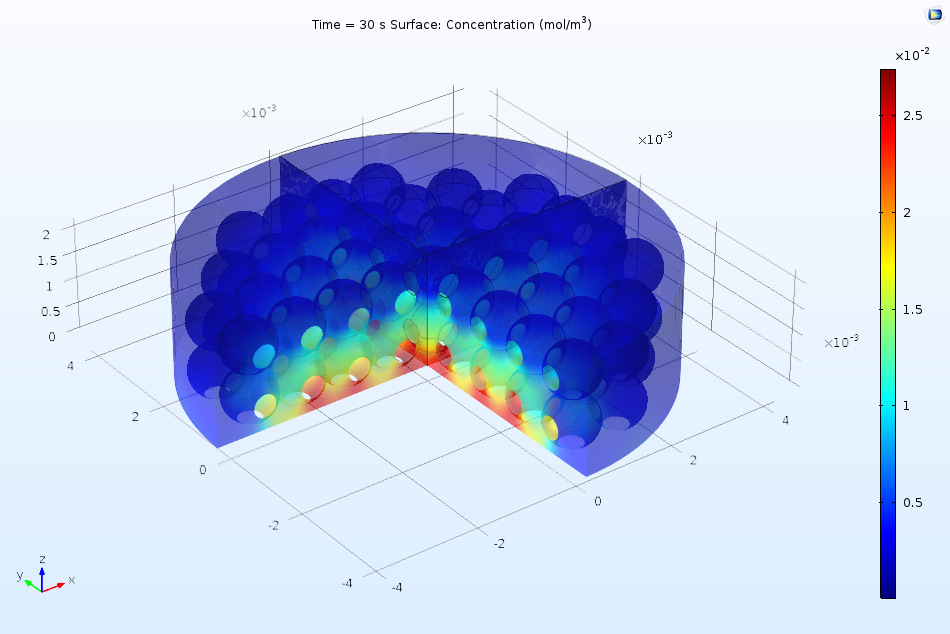
Protein adsorption in an ion exchange column.
Transport and Adsorption
In this example, the diffusion and convection of a species in a solution are described using the Transport of Diluted Species interface. The chemical species also adsorbs at a site on one boundary, where a General Form Boundary PDE is used to express a user-defined equation for surface coverage. This kinetic equation is based on the Langmuir approximation for the adsorption and desorption rates, as discussed above, but does not assume that the reaction attains equilibrium. Hence, the Langmuir isotherm itself does not necessarily hold. Instead, the adsorption and desorption fluxes are considered dynamically.
The figure below shows how the flow of the dissolved adsorbate across the active surface allows the adsorbed surface concentration to gradually increase as time passes. Since the concentrations are still continuing to rise after 2 seconds, it is clear that equilibrium has not yet been attained, so the choice of a kinetic rather than thermodynamic model is appropriate to the description of this surface process. In general, the coverage is higher upstream (to the left) because the concentration in the flow is higher at the upstream end, where less adsorption has already taken place. At the downstream edge, the surface concentration is elevated due to edge effects from diffusion.
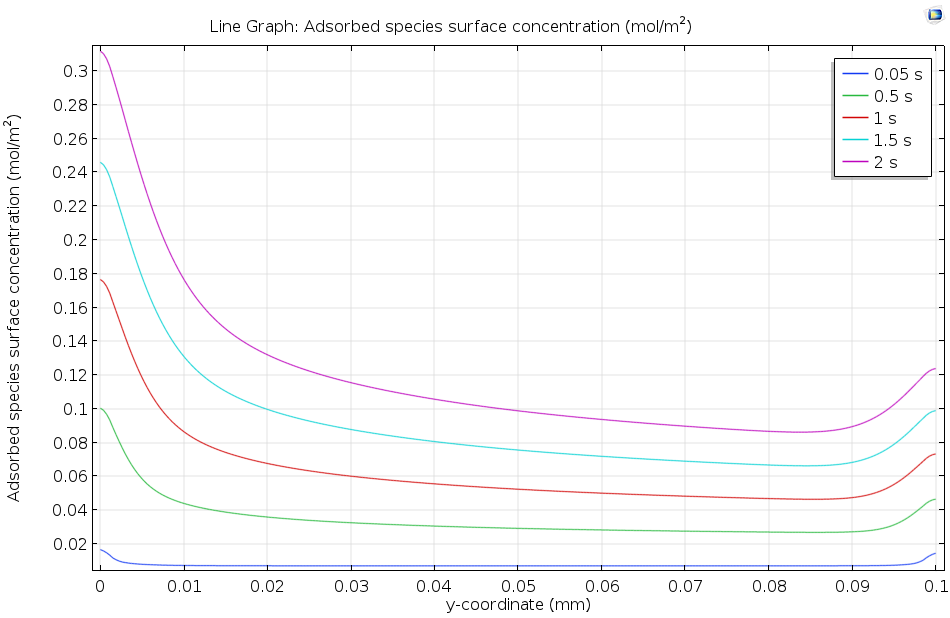
Adsorbed species surface concentration plotted along the length of an active surface over which a solution containing the adsorbate is flowing. As time passes, the adsorbed species concentration increases.
Concluding Thoughts on Surface Modeling
I hope that through this blog series, you’ve learned more about why surfaces are so important to chemistry, as well as the different methods by which surface phenomena can be included in chemical models in COMSOL Multiphysics.
Want to learn more about using COMSOL Multiphysics to model chemical reactions? Contact us to evaluate the software via the button below.
Try It Yourself
Access the three tutorial models featured in this blog post:
Reference
- P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press.







Comments (1)
Nancy Lucero Tapia Ruiz
July 28, 2020Good Nigth Dr. Edmund very interesting this information I would like to know if you have a email where I can contact with you I want to do a simulation of this. Thank you very much for your attention