Modeling Emissivity in Radiative Heat Transfer

When modeling radiative heat transfer, we need to be aware of the concept of surface emissivity and that it can be dependent upon temperature, wavelength, angle, and other variables. Here, we will look into how to model these dependencies using the Heat Transfer Module, and why they can be important for your thermal modeling.

This is the first blog post in a series on modeling radiative heat transfer between surfaces surrounded by a nonparticipating medium. Read Part 2 and Part 3 here.

Background

We begin this discussion with Planck’s law, which is, without hyperbole, one of the fundamental insights of modern physics. It describes the spectral density of radiation from an ideal blackbody, at a known temperature. We can use Planck’s law to plot the spectral blackbody emissive power from a blackbody in free space at increasing temperatures. This shows not only that the emission increases, but also that the peak emission occurs at shorter wavelengths, with increasing temperature. It is also helpful to plot the power normalized with respect to the peak emissive power.

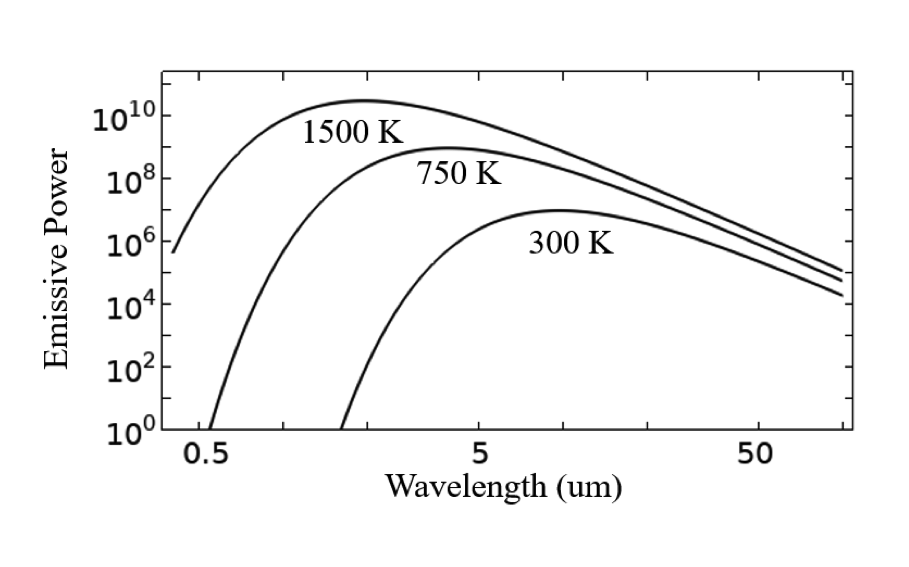
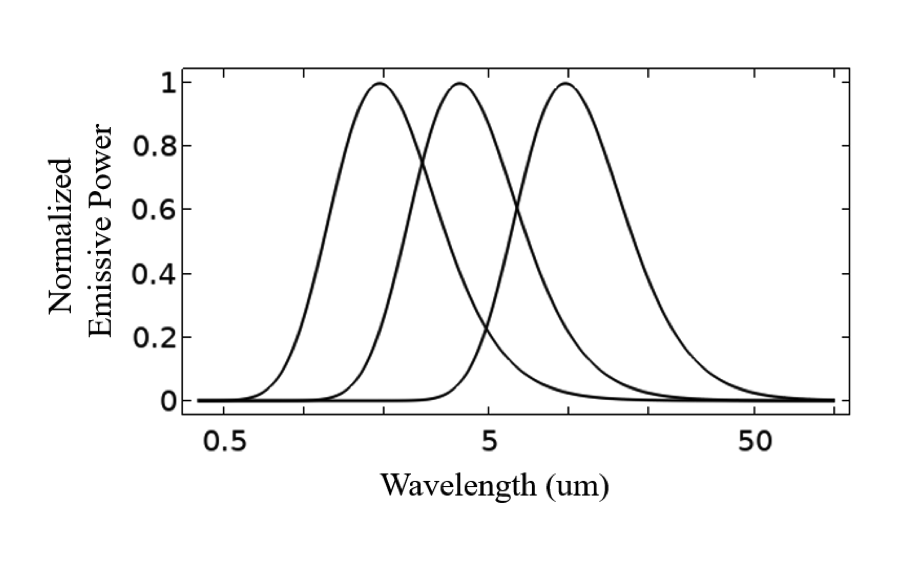
Plot of the blackbody emissive power in log scale (left), and normalized emissive power with respect to peak emission in linear scale (right) as a function of the wavelength in log scale.

If we integrate Planck’s law over all wavelengths, we get the total emissive power of a blackbody, E_b = \sigma T ^4 in free space, where \sigma is the Stefan–Boltzmann constant. Now, although the concept of a blackbody certainly has engineering relevance, all materials deviate from this, so we introduce the concept of emissivity, \epsilon, the ratio between the radiation of a material at a known temperature compared to the radiation of an ideal blackbody. This ratio must always be in the range between zero and one, and we will address here only the cases of opaque materials, where it is possible to say that radiation is emitted from the surface of the material.

Although emissivity is often referred to as a material property, it is a function of both material and surface morphology: A rough surface will have different emissivity as compared to a smooth surface. A thin layer of paint, or a coating or oxidization layer, can also substantially alter the emissivity but have otherwise negligible effects on the thermal behavior. There are tabulated references (for example, Fundamentals of Heat and Mass Transfer by Incropera and DeWitt) of common engineering materials with different surface treatments, but gathering good quality data that covers the complete range of operating conditions is an important step before starting any computational modeling. Before collecting this data, the careful analyst should also know what modeling variables can affect the emissivity, and how that will alter the modeling procedure.

The simplest modeling approach is to treat the emissivity as a constant. This is often good enough for engineering applications where the maximum temperature variation is less than a few tens of kelvin. However, as the temperature of a material changes significantly, its material properties will change, so one needs to consider a variation in emissivity with temperature: \epsilon\left( T \right). Emissivity can also vary significantly with respect to wavelength, \epsilon\left( \lambda\right), for some materials. Although the emissivity will vary continuously with respect to wavelength, for modeling purposes, it is sufficient to divide the spectrum into a finite number of discrete wavelength bands. The choice of these bands depends on both the emissivities of the materials being modeled, as well as the thermal environment. For example, if considering solar environmental loads, it is typical to split up into two bands, the solar and ambient bands, but any number of bands can be considered.

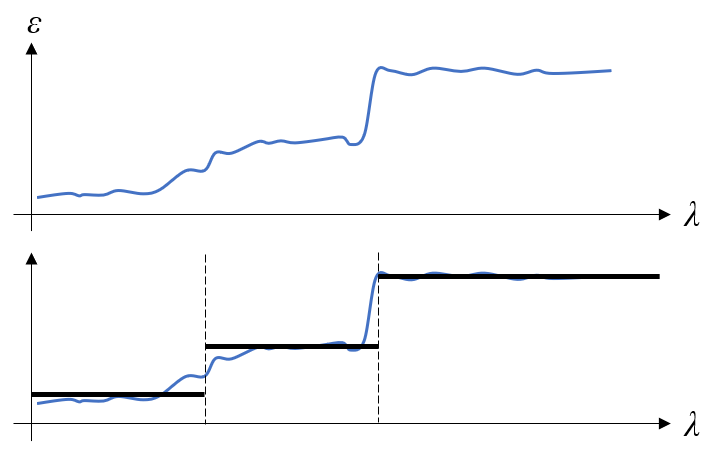
Example of emissivity as a function of wavelength shown in the top figure. This material could be modeled using three bands, as shown in the bottom figure.

It is also important to remark on the averaging approach over the left-most, or right-most, spectral band. Rather than taking a simple average emissivity over these bands, it can be more reasonable to introduce a weighting based on the expected temperature range; for example, ignoring the emissivity over wavelengths where there will be negligible radiation. In practice, there can be many different materials involved, so a fair bit of engineering judgement and approximation as a preanalysis step is warranted when choosing wavelength bands.

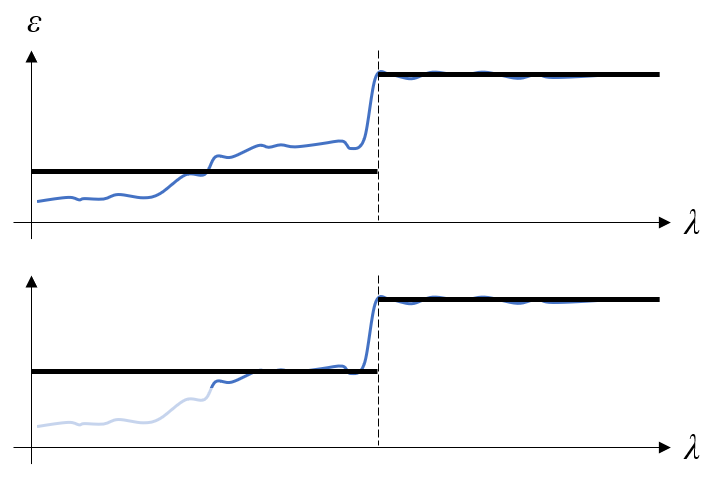
The wavelength-dependent emissivity is reduced to a two-band model. In the top figure, the emissivity is simply averaged within each band. In the bottom figure, the material emissivity at very short wavelengths within the left band is not considered.

It is also possible for the emissivity to vary as a function of angle. Although an ideal blackbody will emit equivalently in all directions, a real surface will have a directional dependence, usually just with respect to the angle from normal, but also possibly with respect to the azimuthal angle when modeling in a three-dimensional space.

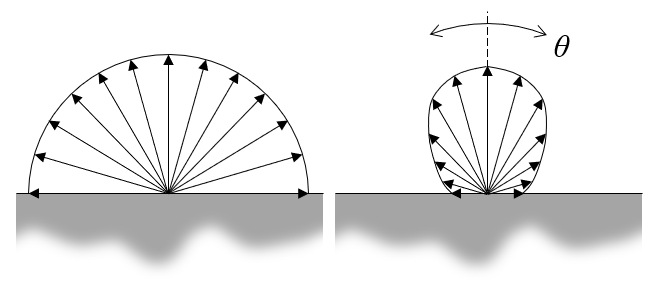
Emissivity can either be isotropic or depend on the angle.

So, it is possible that emissivity is a function of temperature, wavelength, and polar and azimuthal angle: \epsilon\left( T, \lambda, \theta, \phi\right). And, as part of the flexible, interpreted interface of the COMSOL Multiphysics® software, you can additionally introduce a dependency as a function of spatial position or any other model variable. It is also important to remark that the integral of emissivity over all wavelengths and angles will always be less than one for any real material.

Next, let us take a look at how to model some representative cases within the COMSOL software.

Example: Cooling of a Part

We will consider, as an example, the simple situation shown in the figure below. A hot sample of material is centered within a round chamber whose walls are held at fixed temperature, at 0 K. There are no gases present, so all cooling will be radiative. We want to compute how quickly the part cools down and observe the radiative flux incident onto the walls of the chamber. We will assume that the walls of the chamber are an ideal blackbody, thus they can be modeled as having unit emissivity, and since they are at 0 K, this is equivalent to implying that they perfectly absorb the thermal radiation from the part.

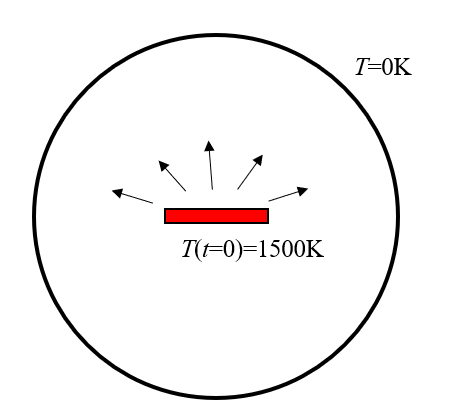
A hot part within a vacuum chamber will cool solely due to radiative heat transfer.

To start, we consider the simplest case of constant emissivity. For this, we set up a Heat Transfer with Surface-to-Surface Radiation model, in a similar approach as demonstrated in the Rapid Thermal Annealing tutorial model. The default settings for this interface assume a single wavelength band and use the Hemicube method to compute view factors.

We exploit symmetry to model only ¼ of the entire structure and specify the appropriate thermal initial and boundary conditions for the Heat Transfer in Solids interface, which is only solved within the domain of the hot part. The Surface-to-Surface Radiation interface is active on the exposed (nonsymmetry) boundaries of the part, as well as the walls of the chamber. The walls of the chamber are modeled as having a constant emissivity of one, representing a perfect absorber, using the Diffuse Surface feature. Within the Diffuse Surface feature, we also fix the wall temperature at 0 K via the Model Input setting, as shown in the screenshot below. That is, we fix the temperature of the chamber wall, and this feature provides a way to evaluate the radiative heat flux.

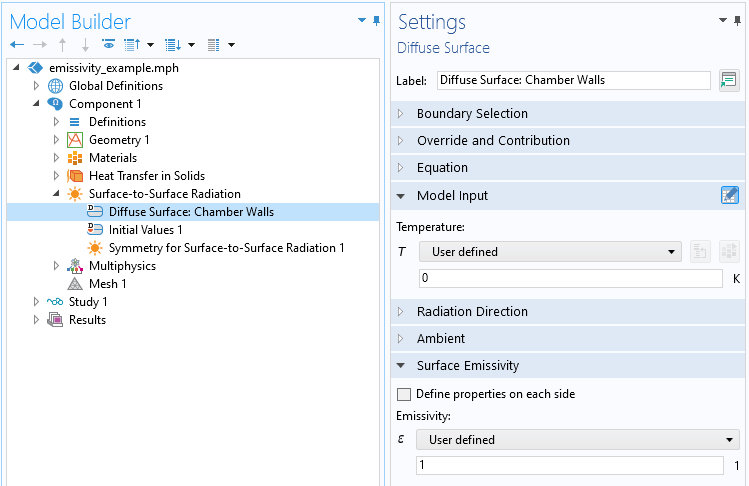
The Diffuse Surface feature defining the walls of the chamber.

We can now turn our attention to modeling the emission from the hot part itself. First, we use the Diffuse Surface feature to specify a constant emissivity for the sample, as shown in the screenshots below. For this boundary condition, the Model Input setting that defines the temperature of the boundary is controlled via the Multiphysics > Heat Transfer with Surface to Surface Radiation feature. That is, the temperature computed via the Heat Transfer in Solids interface defines the surface temperature, and the heat flux computed via the Surface-to-Surface Radiation interface contributes to the boundary flux in the Heat Transfer in Solids interface.

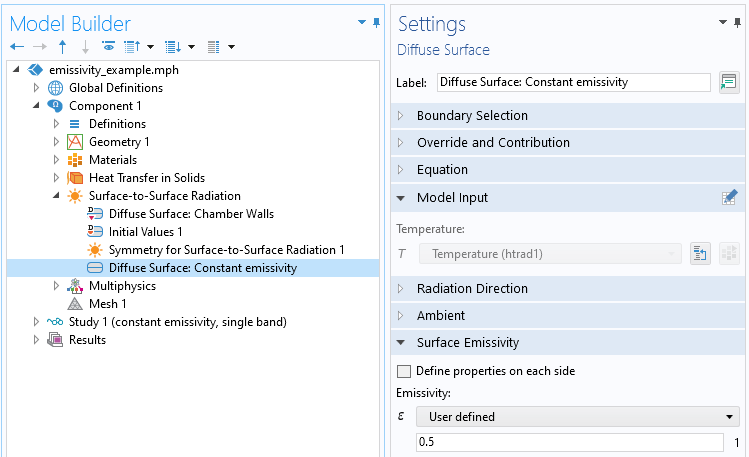
The Diffuse Surface feature defining a constant emissivity of the part. The Model Input section reflects that the temperature is defined from the Heat Transfer in Solids interface.

Next, to modify the emissivity to be a function of temperature, the simplest approach is to enter an expression with respect to the temperature variable, as shown in the screenshot below. It is also possible to define a material property that depends on temperature.

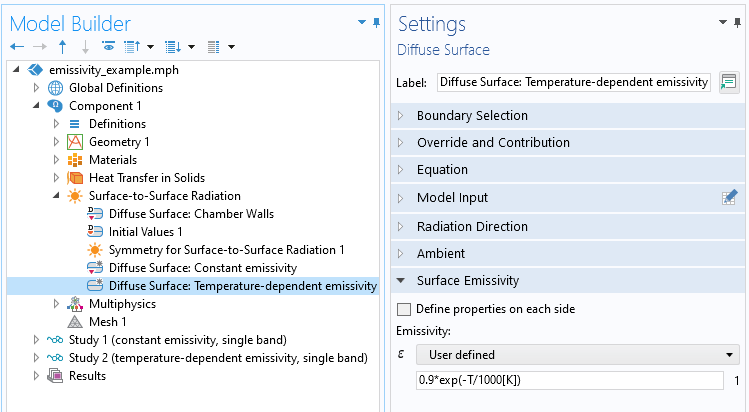
The Diffuse Surface feature with a temperature-dependent emissivity.

To make the emissivity a function of multiple wavelength bands, we modify the Radiation settings and specify wavelengths to delineate the bands. In this case, we will use only two bands, divided at 5 um wavelength as shown in the screenshot below, and specify a different, constant emissivity over each band.

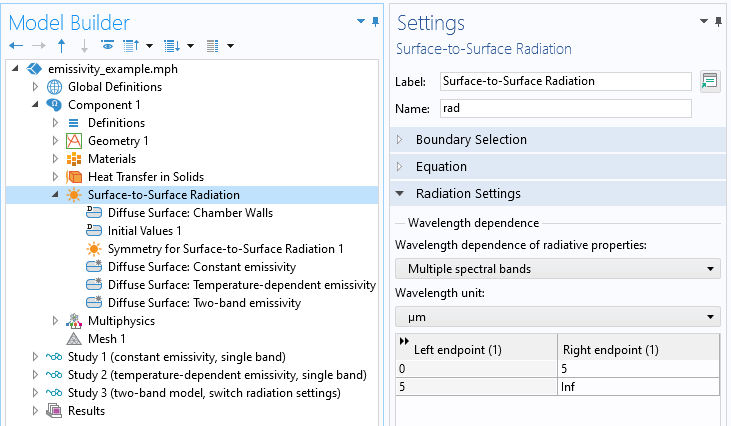
Multiple spectral bands setting.

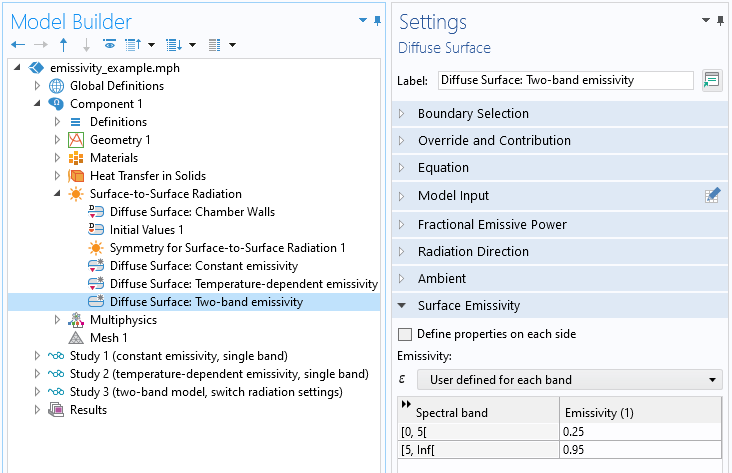
Emissivities specified within each band.

Finally, to consider angular-dependent emissivity, the approach for computing the surface-to-surface radiation must be changed from the Hemicube method to the Ray Shooting method. In the screenshot below, the radiative model is switched back to a one-band model.

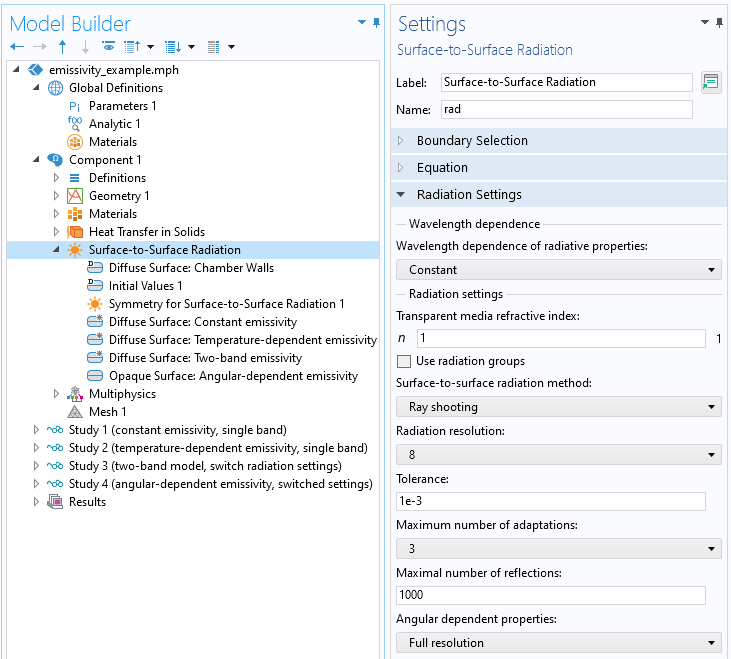
Default Ray Shooting method settings.

When using the Ray Shooting method, the Opaque Surface feature is also available. This feature provides the ability to define a single directional emissivity function, over the entire surface, that is solely a function of angle. The total emissivity of the surface, however, can be a function of temperature, T, position, \mathbf{x}, or any other variable via the surface emissivity expression. The total emissivity is the sum of the directional emissivity function and the surface emissivity expression: \epsilon_{tot} = \epsilon\left(\theta, \phi\right)+\epsilon\left(T, \mathbf{x}, …\right) and different expressions and functions can be used if multiple spectral bands are being used.

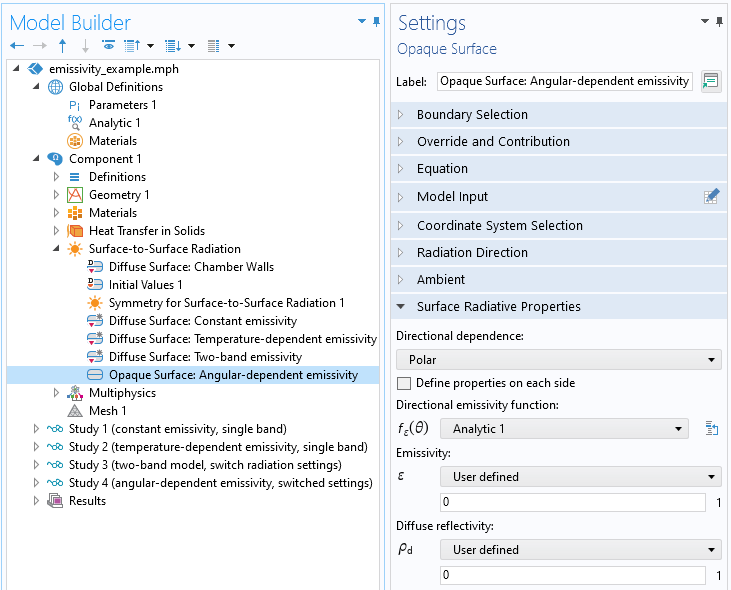
The settings of the Opaque Surface feature. The function defining the directional emissivity is defined within the Global Definitions.

All of these different approaches will lead to slightly different cooling profiles of the part over time, as shown below. It is also interesting to compare the constant emissivity case with the angular-dependent emissivity case, in terms of the radiative flux incident of the chamber walls.

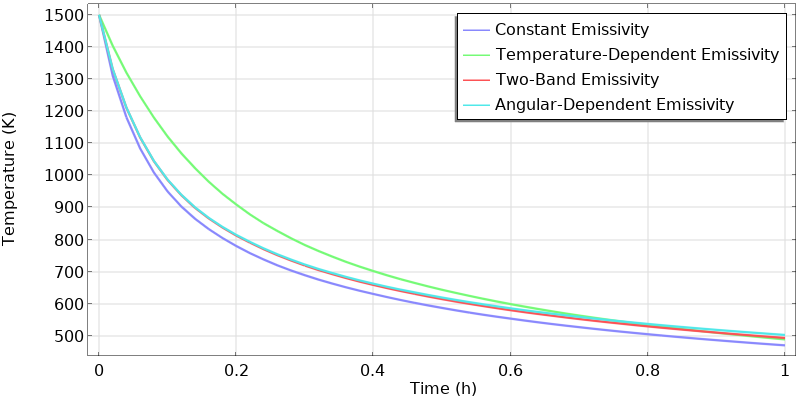
Temperature decay over time of a hot part in a chamber of fixed temperature, computed using different surface emissivity models.

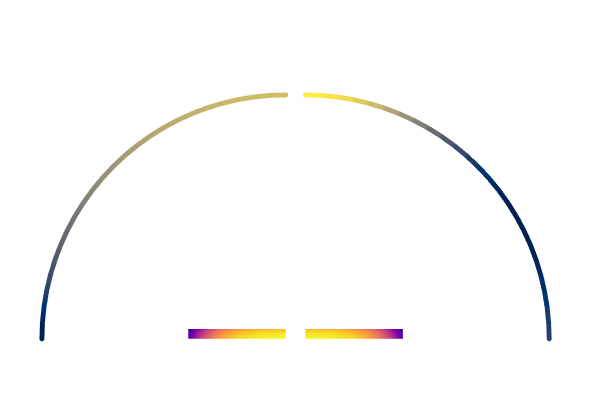
A hot part with constant emissivity (left) versus directional emissivity (right). The flux on the chamber wall is plotted, which highlights the directional nature of the emitted radiation.

It is important to remark that, in this example, with chamber walls being perfect absorbers at 0 K, there is no thermal radiation back toward the part. To round out our understanding of radiative heat transfer, it is also important to understand what happens to thermal radiation impinging upon a surface that is not a perfect absorber. That is the topic we will look at next — so stay tuned!