Modeling Metallic Objects in Wave Electromagnetics Problems

Metals are materials that are highly conductive and reflect an incident electromagnetic wave — light, microwaves, and radio waves — very well. When using the RF Module or the Wave Optics Module to simulate electromagnetics problems in the frequency domain, there are several options for modeling metallic objects. Here, we will look at the Impedance and Transition boundary conditions as well as the Perfect Electric Conductor boundary condition, offering guidance on when to use each one.

What Is a Metal?

When approaching the question of what a metal is, we can do so from the point of view of the governing Maxwell’s equations that are solved for electromagnetic wave problems. Consider the frequency-domain form of Maxwell’s equations:

The above equation is solved in the Electromagnetic Waves, Frequency Domain interface available in the RF Module and the Wave Optics Module. This equation solves for the electric field, \mathbf{E}, at the operating (angular) frequency \omega = 2 \pi f. The other inputs are the material properties: \mu_r is the relative permeability, \epsilon_r is the relative permittivity, and \sigma is the electrical conductivity.

For the purposes of this discussion, we will say that a metal is any material that is both lossy and has a relatively small skin depth. A lossy material is any material that has a complex-valued permittivity or permeability or a non-zero conductivity. That is, a lossy material introduces an imaginary-valued term into the governing equation. This will lead to electric currents within the material, and the skin depth is a measure of the distance into the material over which this current flows.

At any non-zero operating frequency, inductive effects will drive any current flowing in a lossy material towards the boundary. The skin depth is the distance into the material within which approximately 63% of the current flows. It is given by:

where both \mu_r and \epsilon_r can be complex-valued.

At very high frequencies, approaching the optical regime, we are near the material plasma resonance and do in fact represent metals via a complex-valued permittivity. But when modeling metals below these frequencies, we can say that the permittivity is unity, the permeability is real-valued, and the electrical conductivity is very high. So the above equation reduces to:

Before you even begin your modeling in COMSOL Multiphysics, you should compute or have some rough estimate of the skin depth of all of the materials you are modeling. The skin depth, along with your knowledge of the dimensions of the part, will determine if it is possible to use the Impedance boundary condition or the Transition boundary condition.

The Impedance Boundary Condition

Now that we have the skin depth, we will want to compare this to the characteristic size, L_c, of the object we are simulating. There are different ways of defining L_c. Depending on the situation, the characteristic size can be defined as the ratio of volume to surface area or as the thickness of the thinnest part of the object being simulated.

Let’s consider an object in which L_c \gg \delta. That is, the object is much larger than the skin depth. Although there are currents flowing inside of the object, the skin effect drives these currents to the surface. So, from a modeling point of view, we can treat the currents as flowing on the surface. In this situation, it is appropriate to use the Impedance boundary condition, which treats any material “behind” the boundary as being infinitely large. From the point of view of the electromagnetic wave, this is true, since L_c \gg \delta means that the wave does not penetrate through the object.

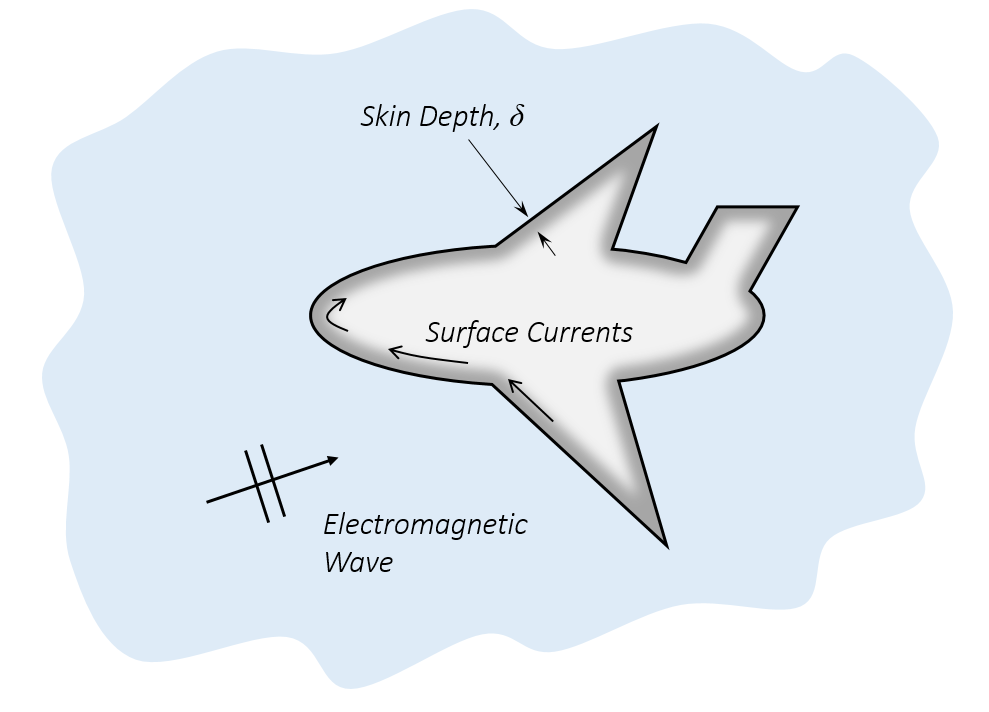
The Impedance boundary condition is appropriate if the skin depth is much smaller than the object.

With the Impedance boundary condition (IBC), we are able to avoid modeling Maxwell’s equations in the interior of any of the model’s metal domains by assuming that the currents flow entirely on the surface. Thus, we can avoid meshing the interior of these domains and save significant computational effort. Additionally, the IBC computes losses due to the finite conductivity. For an example of the appropriate usage of the IBC and a comparison with analytic results, please see the Computing Q-Factors and Resonant Frequencies of Cavity Resonators tutorial.

The IBC becomes increasingly accurate as L_c / \delta \rightarrow \infty; however, it is accurate even when L_c / \delta \gt > 10 for smooth objects like spheres. Sharp-edged objects such as wedges will have some inaccuracy at the corners, but this is a local effect and also an inherent issue whenever a sharp corner is introduced into the model, as discussed in this previous blog post.

Now, what if we are dealing with an object that has one dimension that is much smaller than the others, perhaps a thin film of material like aluminum foil? In that case, the skin depth in one direction may actually be comparable to the thickness, so the electromagnetic fields will partially penetrate through the material. Here, the IBC is not appropriate. We will instead want to use the Transition boundary condition.

The Transition Boundary Condition

The Transition boundary condition (TBC) is appropriate for a layer of conductive material with a thickness relatively smaller than the characteristic size, and curvature, of the objects being modeled. The TBC can be used even if the thickness is many times greater than the skin depth.

The TBC takes the material properties as well as the thickness of the film as inputs, computing an impedance through the thickness of the film as well as a tangential impedance. These are used to relate the current flowing on the surface of either side of the film. That is, the TBC will lead to a drop in the transmitted electric field.

From a computational point of view, the number of degrees of freedom on the boundary is doubled to compute the electric field on either surface of the TBC, as shown below. Additionally, the total losses through the thickness of the film are computed. For an example of using this boundary condition, see the Beam Splitter tutorial, which models a thin layer of silver via a complex-valued permittivity.

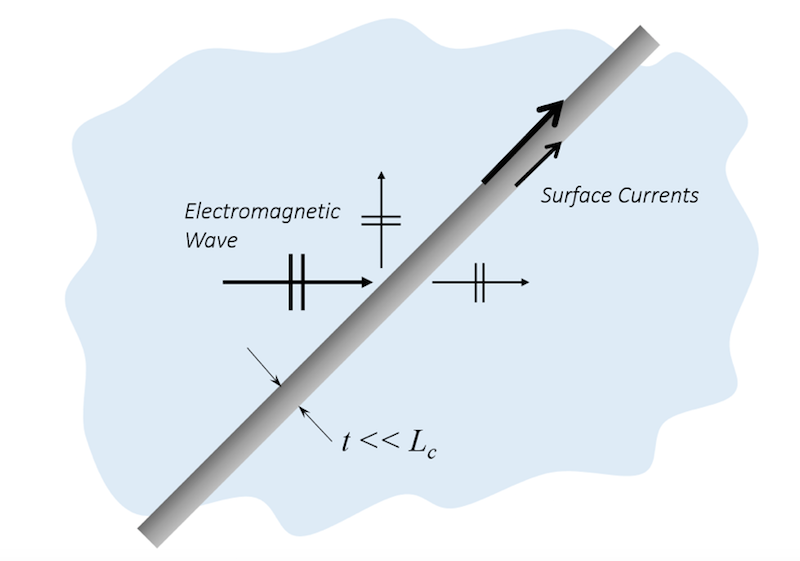
The Transition boundary condition computes a surface current on either side of the boundary.

Adding Surface Roughness

So far, with both the TBC and the IBC, we have assumed that the surfaces are perfect. A planar boundary is assumed to be geometrically perfect. Curved boundaries will be resolved to within the accuracy of the finite element mesh used, the geometric discretization error, as discussed here.

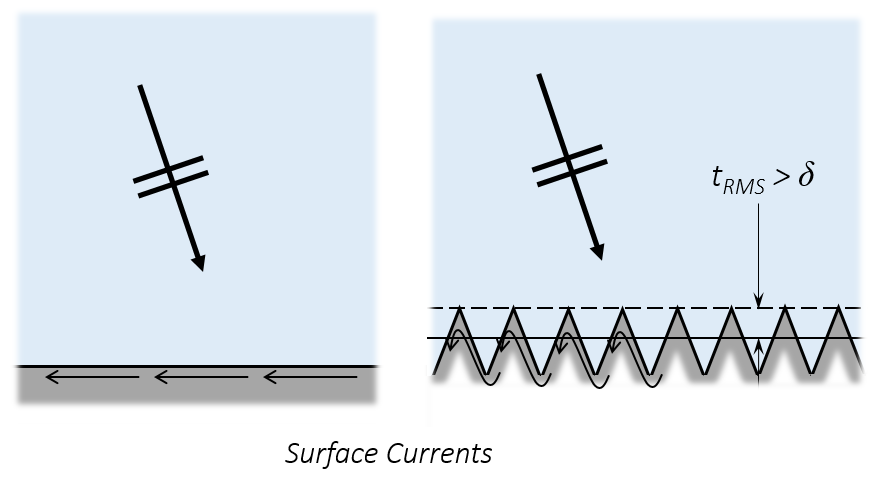
Rough surfaces impede current flow compared to smooth surfaces.

All real surfaces, however, have some roughness, which may be significant. Imperfections in the surface prevent the current from flowing purely tangentially and effectively reduce the conductivity of the surface (illustrated in the figure above). With COMSOL Multiphysics version 5.1, this effect can be accounted for with the Surface Roughness feature that can be added to the IBC and TBC conditions.

For the IBC, the input is the Root Mean Square (RMS) roughness of the surface height. For the TBC, the input is instead given in terms of the RMS of the thickness variation of the film. The magnitude of this roughness should be greater than the skin depth, but much smaller than the characteristic size of the part. The effective conductivity of the surface is decreased as the roughness increases, as described in “Accurate Models for Microstrip Computer-Aided Design” by E. Hammerstad and O. Jensen. There is a second roughness model available, known as the Snowball model, which uses the relationships described in The Foundation of Signal Integrity by P. G. Huray.

The Perfect Electric Conductor Boundary Condition

It is also worth looking at the idealized situation — the Perfect Electric Conductor (PEC) boundary condition. For many applications in the radio and microwave regime, the losses at metallic boundaries are quite small relative to the other losses within the system. In microwave circuits, for example, the losses in the dielectric substrate typically far exceed the losses at any metallization.

The PEC boundary condition is a surface without loss; it will reflect 100% of any incident wave. This boundary condition is good enough for many modeling purposes and can be used early in your model-building process. It is also sometimes interesting to see how well your device would perform without any material losses.

Additionally, the PEC boundary condition can be used as a symmetry condition to simplify your modeling. Depending on your foreknowledge of the fields, you can use the PEC boundary condition, as well as its complement — the Perfect Magnetic Conductor (PMC) boundary condition — to enforce symmetry of the electric fields. The Computing the Radar Cross Section of a Perfectly Conducting Sphere tutorial illustrates the use of the PEC and PMC boundary conditions as symmetry conditions.

Lastly, COMSOL Multiphysics also includes Surface Current, Magnetic Field, and Electric Field boundary conditions. These conditions are provided primarily for mathematical completeness, since the currents and fields at a surface are almost never known ahead of time.

Summary

In this blog post, we have highlighted how the Impedance, Transition, and Perfect Electric Conductor boundary conditions can be used for modeling metallic surfaces, helping to identify situations in which each should be used. But, what if you cannot use any of these boundary conditions? What if the characteristic size of the parts you are simulating are similar to the skin depth? In that case, you cannot use a boundary condition. You will have to model the metal domain explicitly, just as you would for any other material. This will be the next topic we focus on in this series, so stay tuned.