
One of the challenges of room acoustics, regarding modeling and simulation, is accurately modeling a room over the entire frequency range. This blog discusses a hybrid approach for modeling room acoustics in the COMSOL Multiphysics® software where the results from multiple methods are integrated into a single model, thereby improving accuracy and maintaining feasibility. Let’s learn how this can be done.
Review of Room Acoustics
In a previous blog post on modeling room acoustics with COMSOL Multiphysics, we described multiple methods available in the Acoustics Module that can be used to model the acoustics of enclosed spaces. The post discussed how to model:
- Modal behavior with the Pressure Acoustics interface
- High-frequency behavior with the Ray Acoustics interface
- High-frequency behavior with the Acoustic Diffusion Equation interface
Today, we will discuss how the first two methods can be combined to obtain a broadband impulse response for a room.
Room Impulse Response
Imagine an air-filled balloon is popped in a room while a microphone at some other location in the room records the acoustic pressure as a function of time. The microphone will receive direct sound from the first wavefront as well as a superposition of all reflected signals from the waves traveling and bouncing off the walls, floor, ceiling, and other objects in the room. Sound is typically absorbed by different materials, like those of any carpet, furniture, and ceiling tile for example, meaning the sound will eventually die down completely until it is quiet again. The acoustic pressure versus time signal recorded by the microphone is called the room impulse response at that measured location. This is an extremely important room acoustic descriptor, as it can tell a lot about how the room will sound.
Left: Results from a ray acoustics model show the paths of a fraction of the rays from a sound source to a microphone location. Right: A room impulse response example.
Modeling the Room
When modeling the acoustics of a room, a simulation engineer must pay attention to both the acoustic and geometric scales in order to determine the accuracy and feasibility of a modeling approach. In the Acoustics Module, the low-frequency, modal behavior of a room can be modeled with the finite element method using the Pressure Acoustics, Frequency Domain interface. However, this approach becomes computationally expensive at high frequencies due to mesh requirements. The high-frequency, reverberant behavior of rooms can be modeled with the ray-tracing method using the Ray Acoustics interface. While this method is typically computationally efficient, ray tracing is not a wave-based method and will not capture modal behavior. To accurately model the impulse response of a room, both models can be run in their respective frequency ranges and combined to obtain the response over the entire frequency range.
Let’s consider a rectangular room that is 4.7 x 4.1 x 3.1 m. All walls in this example are modeled with a frequency-dependent absorption coefficient. The goal of the model is to determine the impulse response at a microphone located at coordinates (3,3,2) m. It turns out that for a monopole impulsive source considering “lightly” absorbing walls, there is an analytical solution in three dimensions for the pressure at any point in the room. Following the notation of Ref. 1 and Ref. 2, the pressure P(r) at any point can be expressed in terms of the Green’s function G(r,r_0), which is constructed from undamped room mode shapes evaluated at the receiver (r) and source (r0) positions and a frequency-dependent damping term \tau_{mnp}. The expressions are:
Here, \rho_0 is the density, \omega is the frequency, and Q is the monopole domain source volume velocity. The Green’s function represents a triple summation over modes in the three orthogonal cartesian directions, with indices m n p representing the different modes. The \psis represent mode shapes, a product of cosine functions, of the modes k_{mnp}, and \Lambda_{mnp} is a mode integer factor for the room of volume V. The wavenumber is k. For a complete description of the analytical solution, see Ref. 1 and Ref. 2. For this modeling scenario, the variables that define the analytical solution have been added in Component 1 > Definitions > Variables 1 – Analytical Solution.
As discussed in this previous blog post, there is no clear-cut transition frequency between the modal and reverberant room behavior, but it can be estimated based on criteria proposed by Schroeder (Refs. 3, 4). For this case, the Schroeder frequency is close to 370 Hz, and is computed in Global Definitions > Ray Parameters. The analytical solution above will serve as a reference solution to compare to the numerical model.
Pressure Acoustics
Ideally, we might like to model the room using wave-based methods throughout the whole frequency range, but this may not be feasible at high frequencies due to mesh requirements. Since we know that the contribution of individual modes dominates the room response below the Schroeder frequency, we will choose to solve the pressure acoustics using a maximum frequency that is a bit higher than the Schroeder frequency: up to 500 Hz in this case. The setup of the pressure acoustics model includes:
- A 3D component with the Pressure Acoustics, Frequency Domain interface
- A monopole point source with constant power
- Walls prescribed with a frequency-dependent impedance condition (absorption coefficient)
- A volume mesh that resolves the wavelength in air at 500 Hz
- A frequency domain study
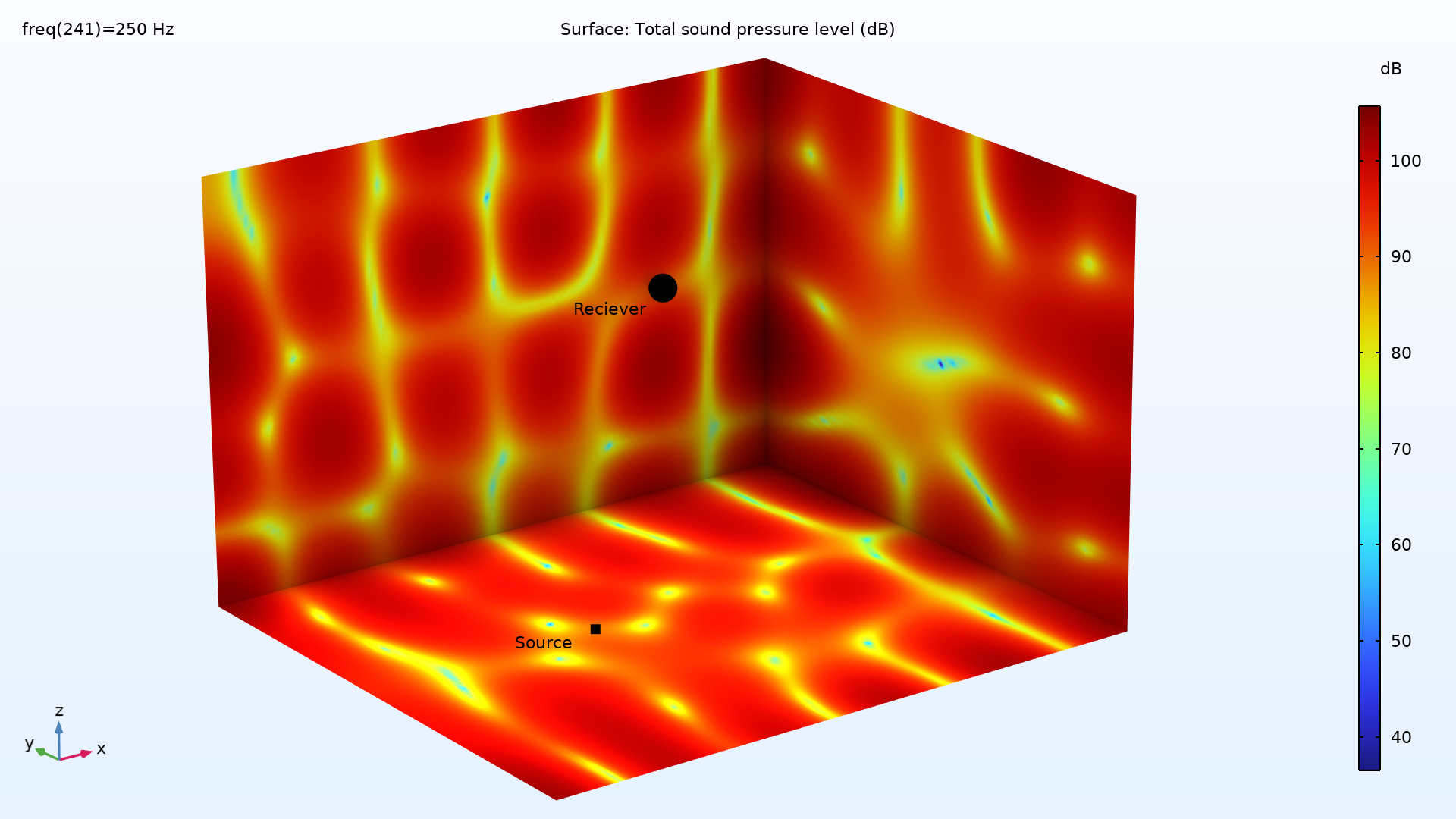
Sound pressure level (dB ref. 20 µPa) on three walls of the rectangular room at 250 Hz.
The plot above shows an example of the total sound pressure level distribution on some of the walls in the room. Using this method, the low-frequency behavior (below 500 Hz) of the room has now been modeled. To model the high-frequency behavior of the room, we will switch to ray acoustics.
Ray Acoustics
The ray acoustics model is set up with the following:
- A 3D component with the Ray Acoustics interface
- Walls prescribed with a frequency-dependent absorption coefficient
- A Release from Grid condition to release 8000 rays from the source point with a prescribed power
- A Ray Termination criteria to stop tracing rays (thereby reducing degrees of freedom) if the power levels decrease below a threshold value
- A ray-tracing study with a parametric sweep over 1/3 octave band frequencies up to 4000 kHz
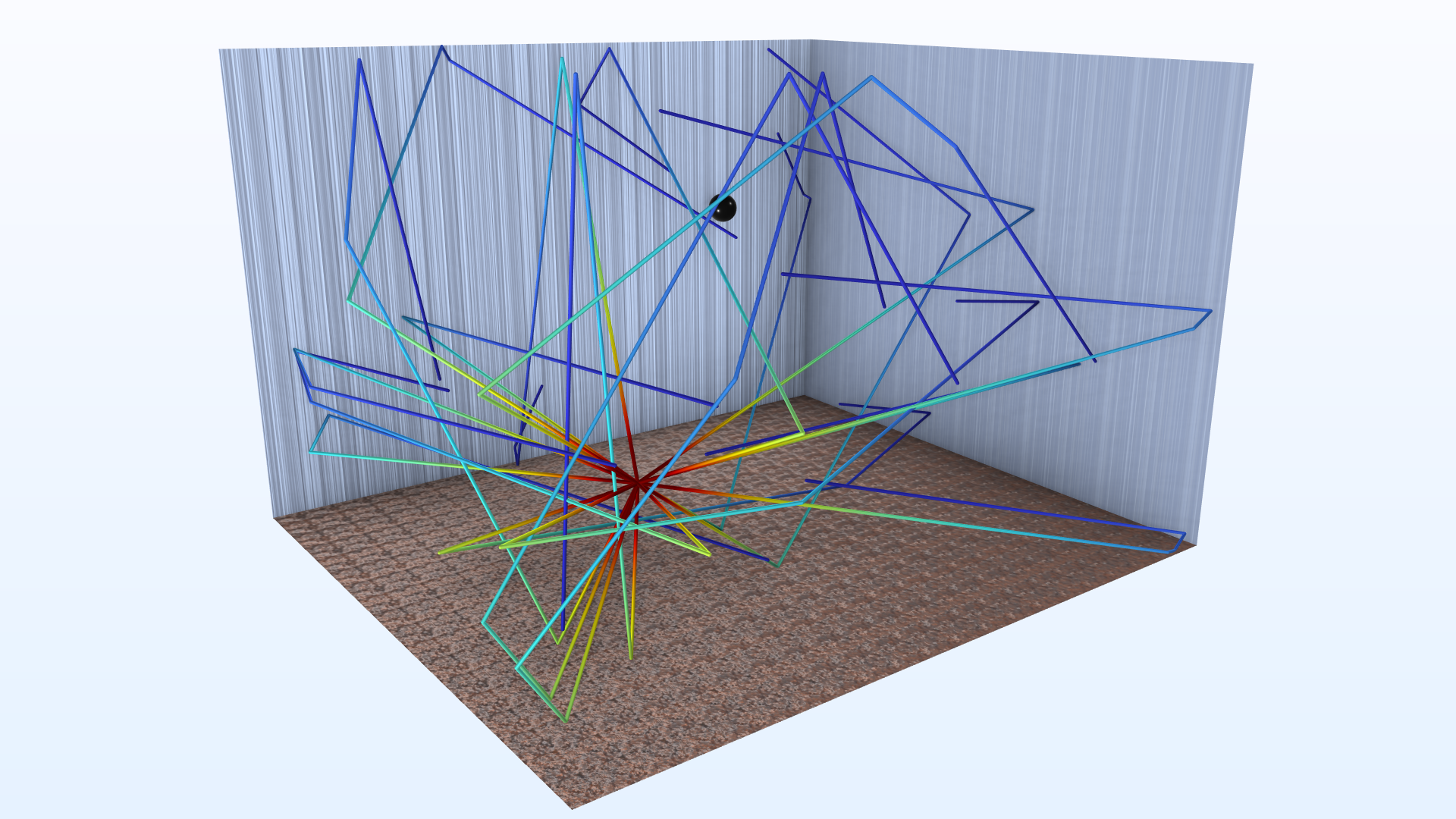
The image below shows a snapshot in time of the rays released from the point source. Note that only a fraction of the rays are shown below for visualization purposes. (Rays with a y-coordinate less than the source position are hidden.)

Ray trajectories at 3 ms showing the ray release from the monopole point source. The color scale represents ray pressure in Pa.
The ray-tracing study is not run over fine steps in frequency. So how is the impulse response computed? In COMSOL Multiphysics, there is a dedicated Receiver dataset and Impulse Response 1D plot group for this. This plot group takes the 1/3 octave band inputs, such as ray power, frequency, number of reflections, and fluid properties, and reconstructs an impulse response over frequency. The goal is to obtain a new signal that has the same energy content as the true signal when averaged over the input octave bands. This is done by convolving the impulse signal with a selected IR filter kernel (the default is a brick-wall with Kaiser window) and then summing up the contributions from all rays over all frequency bands. For more information on the reconstruction, view the Acoustics Module User’s Guide.
The plot below shows the sound pressure level at the microphone location. Since the monopole point source represents an impulse in time, the room impulse response can also be interpreted in the frequency domain where the source is a broadband excitation over frequency. (The Fourier transform of a Dirac delta function in time is a constant function of frequency.)
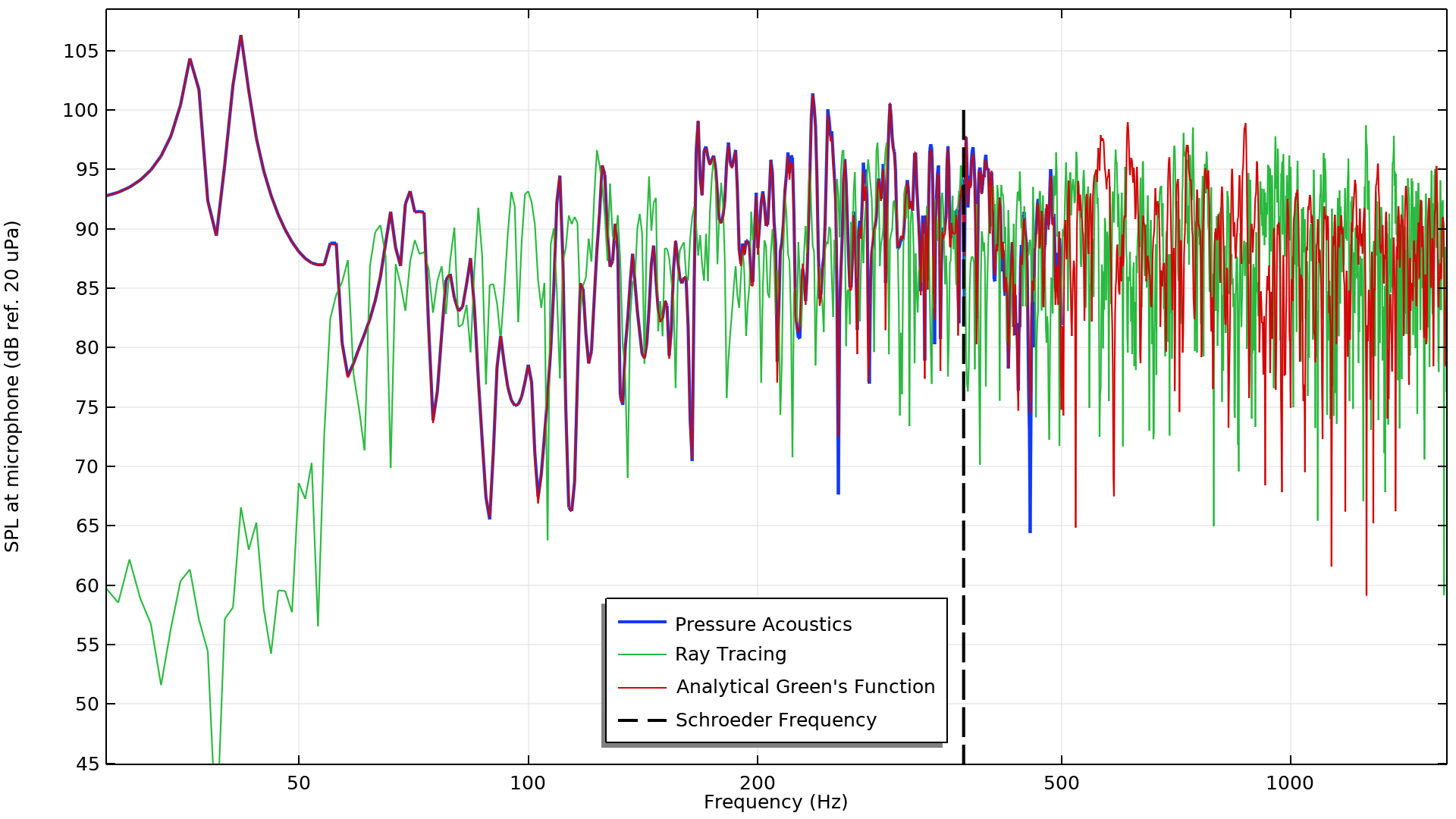
Sound pressure level at the microphone as computed by the pressure acoustics study, ray-tracing study, and the analytical formula. The dashed black line represents the Schroeder frequency.
Based on this plot, we can draw a few key conclusions. First, the analytical result matches well with the pressure acoustics study result up to 500 Hz, which was the maximum frequency in that study. This result serves as a good benchmark that the model was set up correctly.
When comparing the ray-tracing result to the other results, it is clear that the low-frequency sound pressure levels do not match. These results are as expected, since ray tracing is not a wave-based method inherently and does not capture the modal behavior that dominates at low frequency. We can conclude that the ray-tracing results are not accurate at low frequency, especially below 50 Hz in this model.
The first two resonant peaks in the pressure acoustics plot correspond to two different modes that have been excited by the impulsive source and whose acoustic energy has not been strongly absorbed by the walls. Since we considered light absorption in the model, the modes here are nearly equal to the modes of a room with sound hard walls. Ref. 5 derives and computes the first 20 modes of the same sized room (4.7 x 4.1 x 3.1 m) considering rigid boundary conditions (see Table 3.1 in Ref. 5). The first two modes are the (1,0,0) mode at 36.17 Hz and the (0,1,0) mode at 41.46 Hz. These correspond to the first mode in the x– and y-directions, respectively, and align well with the first two peaks on the plot above.
There are 20 modes below 117 Hz, and, as frequency increases, there is an increasing number of modes that contribute to the reverberant behavior of the room. At low frequencies, the modes are spaced far apart and the bandwidths of the modes do not overlap. At high frequencies, the modes do overlap, which leads to a noisy-looking frequency response. Because ray tracing is not a wave-based method, the results from ray tracing are not expected to match exactly the analytical result, even above the Schroeder frequency. However, both the ray-tracing and analytical results show similar characteristics and ranges of sound pressure level above the Schroeder frequency. This means that the ray-tracing results above the Schroeder frequency can be used to accurately estimate the impulse response based on the criteria of maintaining the same energy content as the true signal when averaged over the input octave bands.
Combination Method
The results from the pressure acoustics and ray acoustics models can be combined to create a broadband impulse response signal. Similar to the method described in Ref. 6, this can be done by taking a low-pass filtered pressure acoustics response and adding it to the high-pass filtered ray acoustics response. This method leverages the linearity property of the Fourier transform.
The type of filter used and the designation of where to filter the signals is not set by any engineering standard. The implemented digital signal processing technique can be selected based on industry-specific practice or engineering judgment. This model demonstrates the combination concept using simple ideal step filters that filter the signal at the Schroeder frequency.
The signal combination is set up as follows:
- A 0D component with the Global ODEs and DAEs interface
- Results from the Ray Acoustics model are exported to files and imported into Component 3 as interpolation curves
- Results from the Pressure Acoustics model are passed to Study 3 using Values of Dependent Variables in the study settings
The following Global Equations are added to Component 3:
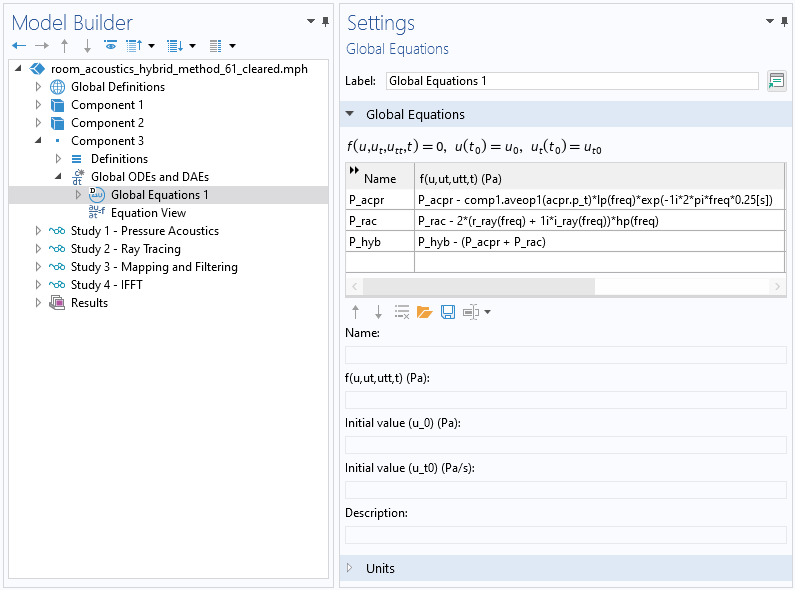
The Global Equations added to Component 3.
Here, P_acpr is the volume-averaged pressure at the receiver. The expression shows that the pressure is low-pass filtered and shifted in time (by 0.25 s) in order to match the convention in the Impulse Response plot type for later comparison. P_rac is the pressure from interpolation functions of the impulse response fast Fourier transform (FFT). The P_rac expression uses the interpolation functions r_ray and i_ray — the real and imaginary parts of the pressure from the ray-tracing study, Study 2. The pressure expression also indicates that the ray pressure is high-pass filtered and multiplied by two. The factor of two is due to only positive frequency being computed in Study 3, while the interpolation values are for the full spectrum. Finally, P_hyb is the summation of the low-pass filtered pressure acoustics response and the high-pass filtered ray-tracing response (using a similar approach to that used in Ref. 6).
The plot below shows a comparison of the original and combined signals after running a frequency domain study with only Component 3. Here, we can see that the hybrid response has the correct frequency content from combining both the pressure acoustics and ray-tracing results.
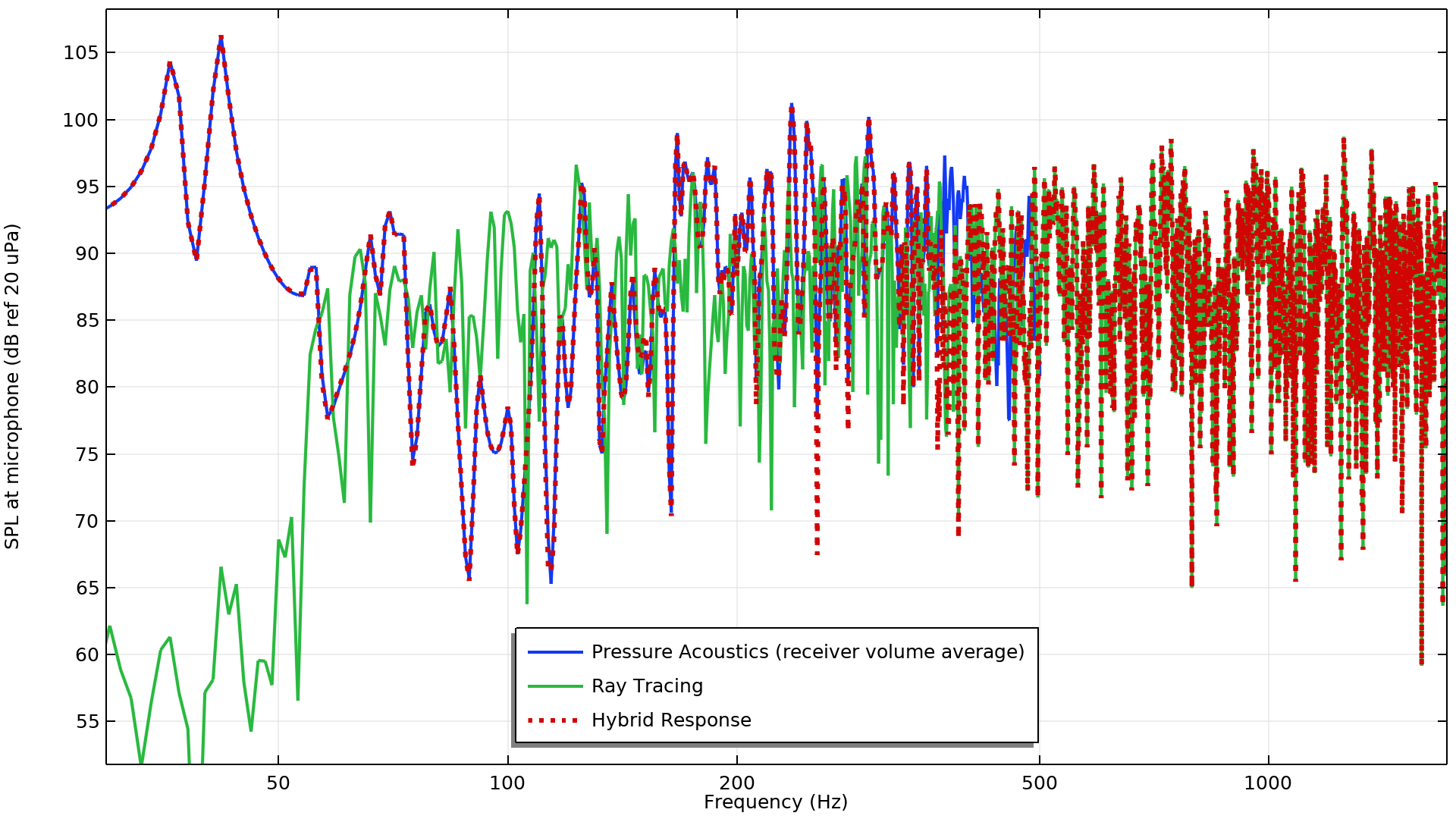
Sound pressure level at the microphone as computed by the pressure acoustics, ray-tracing, and hybrid methods.
The ideal filters are implemented using step functions, stepping from 0 to 1 for the high-pass filter hp(freq) and stepping from 1 to 0 for the low-pass filter lp(freq). A 50 Hz smoothed transition zone has been included in both functions and the location of the step transition is set to the Schroeder frequency. Both of these functions are added under Component 3 > Definitions. A closer look at the hybrid response near the Schroeder frequency is shown in the figure below. From the plot we can analyze the characteristics of the ideal filters. In particular, the ideal filters both have a gain factor of -3 dB at the Schroeder frequency, meaning the response here is an average of both. Elsewhere, the hybrid response is a weighted combination of both responses, depending on the frequency. The sum of the filters is 0 dB over all frequency.
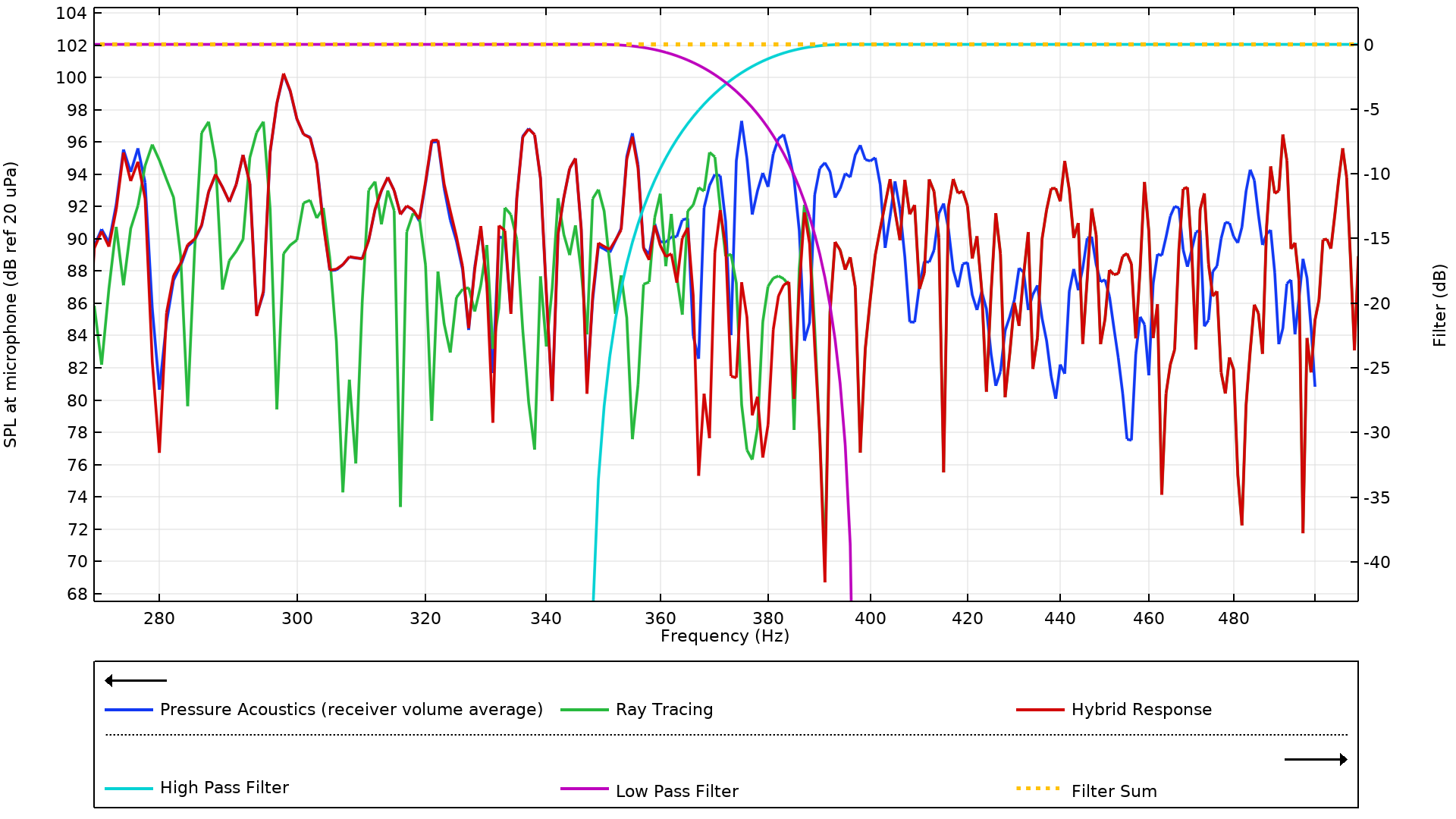
Filter-averaged hybrid pressure near the Schroeder frequency.
To bring the response back to the time domain, a fourth and final study is run, which includes a frequency-to-time FFT step. In this step, a Tukey window function is used to band-limit the inverse FFT (IFFT). A comparison of the hybrid signal and the original ray-tracing signal is shown below. Although we can see some differences in the time domain, it is easier to spot differences by looking directly at the frequency spectrum. It’s clear that the hybrid pressure versus time signal computed here is more accurate than the pure ray-tracing signal over the entire frequency range. This accuracy means that the hybrid signal can be used to compute other room metrics, such as the clarity, reverberation times, or speech transmission index, or exported to be used in an external analysis tool for room auralization.
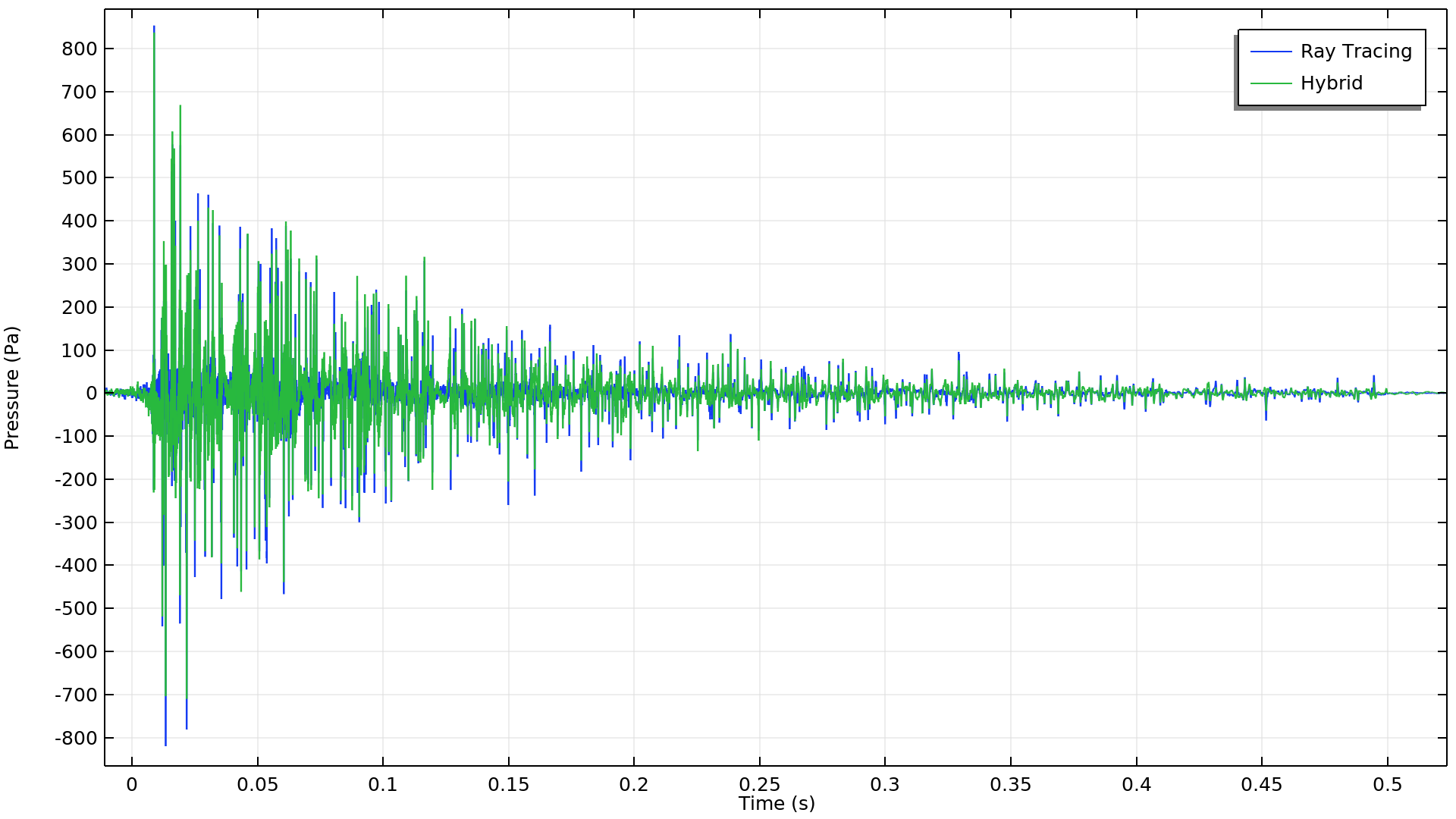
Pressure versus time impulse response comparison between the ray-tracing and hybrid method.
Try It Yourself
Here, we have shown one approach for obtaining a broadband impulse response by combining ray-tracing and finite element methods. All of the modeling is completed in COMSOL Multiphysics, and the solutions are integrated into a single model. The approach is especially useful for large rooms where using full-wave methods at high frequencies may not always be feasible. Try it yourself by clicking the button below, where you can download the model files from the Application Gallery:
Further Resources
If you would like to see more room acoustics models, you can check out these related models in our Application Gallery:
- Chamber Music Hall: the acoustics of the Small Hall in the Konzerthaus Berlin is simulated with ray tracing.
- Car Cabin Acoustics – Frequency Domain Analysis: the interior acoustics of a car cabin is modeled using pressure acoustics. An iterative solver is used to solve the model up to 4 kHz.
References
- Morse, Philip McCord, and K. Uno Ingard. Theoretical Acoustics. Princeton University Press, 1986.
- Okoyenta, Augustus R., et al. “A Short Survey on Green’s Function for Acoustic Problems.” Journal of Theoretical and Computational Acoustics 28.02 (2020): 1950025.
- M. R. Schroeder, New Method of Measuring Reverberation Time, J. Acoust. Soc. Am., 37 (1965).
- M. R. Schroeder, Integrated-Impulse method measuring sound decay without using impulses, J. Acoust. Soc. Am., 66 (1979).
- Kuttruff, Heinrich. Room Acoustics. CRC Press, 2016.
- Aretz, Marc, et al. “Combined broadband impulse responses using FEM and hybrid ray-based methods.” EAA Symposium on Auralization, 2009.




Comments (2)
Mathias Barbagallo
March 1, 2023Hello,
can this be done using DGFem + Ray tracing?
If yes, why would one want to use FEM, frequency domain as you did, instead?
Cheers
Mathias
Mark Cops
March 3, 2023 COMSOL EmployeeHi Mathias,
Yes, dG-FEM can also be used to model the room and will capture the modal behavior. We actually have a full-wave time domain room acoustics model in the application gallery that uses that method (https://www.comsol.com/model/full-wave-time-domain-room-acoustics-with-frequency-dependent-impedance-90551). In this blog, since we are primarily interested in modeling a limited frequency range with Pressure Acoustics, standard finite elements are a good candidate here since the wavelength remains approximately the same scale as the room dimension. Furthermore in the frequency domain it easier to model frequency dependent absorption and one does not need to take small time steps and run the simulation in time until the impulse dies out.