
Maintaining an even temperature for buildings in hot climates often requires a lot of energy. One option for improving thermal performance is by including phase change materials (PCMs) in parts of the building. To study the effectiveness of PCMs in regulating temperature, researchers used the COMSOL Multiphysics® software to model a novel plaster that includes a PCM. They then analyzed the thermal performance of the PCM-enhanced plaster and compared the results with a reference plaster.
Using PCMs to Improve the Thermal Performance of Buildings
Active thermal control systems in buildings help keep people comfortable in extreme weather conditions. For example, these systems can maintain a steady temperature indoors in places that are “summer dominant”, which are often very warm during the day and quite cool at night. However, active thermal control systems consume a lot of energy. They are also expensive to run around the clock, making them a less-than-ideal solution for keeping a steady interior temperature in such climates.
Passive thermal control systems are more efficient. One advantage of these systems is that they can run on less energy. They can also work with active thermal control systems, which minimizes the energy needed to maintain an even temperature. Further, passive thermal control systems can be included in a building during construction, helping to lower energy consumption costs over the lifetime of the structure.

A bedroom in the process of being remodeled. The walls are covered in a standard plaster.
Using phase change materials (PCMs) in building elements is one method of passive thermal control. As PCMs change phase, they begin to absorb or release their latent energy within a small temperature range, depending on whether they are in their liquid or solid phase, respectively. In doing so, they increase the thermal inertia of a building. Since PCMs can provide or store heat as needed, using them in buildings is particularly advantageous in areas with large daily temperature changes. This ability is less useful in climates that are constantly hot, as the PCM also stays hot.
To optimize PCMs for use in buildings, a research team from the Frederick Research Center, Cyprus, and University of Cyprus used numerical simulation.
Modeling the Novel PCM-Enhanced Plaster with Numerical Simulation
To study the thermal performance of a PCM in a building element, the researchers created a 3D model consisting of a concrete block with a layer of plaster. They added a PCM to the plaster in different weight amounts:
- 5%
- 10%
- 20%
It is important that the PCM can adjust with the temperature changes in hot climates. For this reason, Micronal 5038X was used as the PCM, as it has a melting temperature of 26˚C. To see how effective the PCM is in managing temperature, the model also includes a reference plaster to act as a comparison.
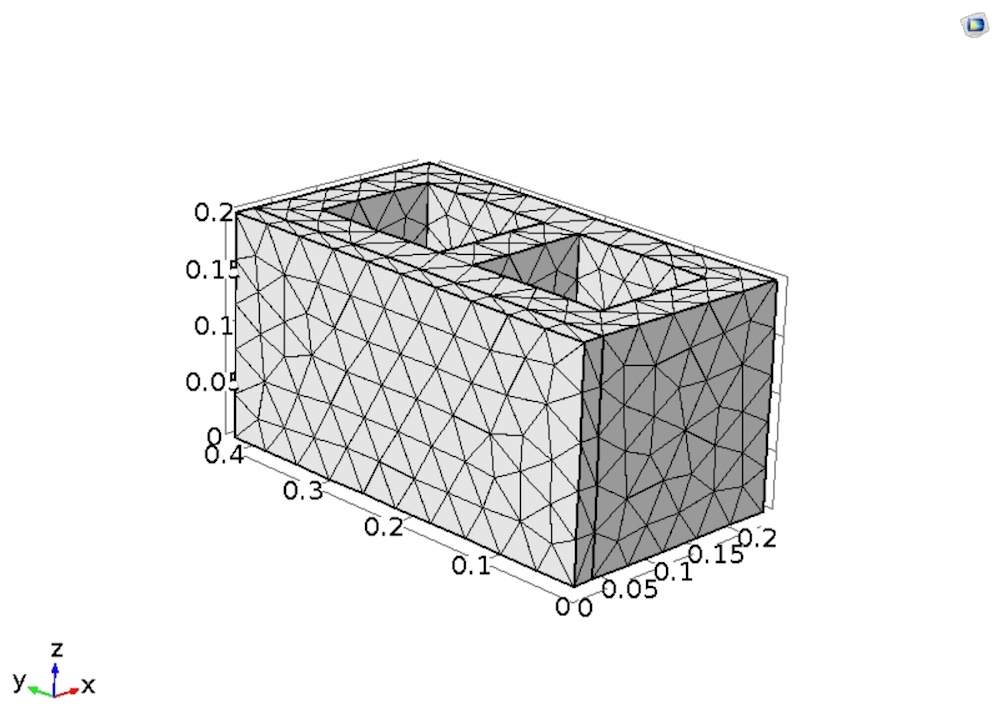
The geometry of the building element. Image courtesy A. Kylili, M. Theodoridou, I. Ioannou, and P.A. Fokaides and taken from their COMSOL Conference 2016 Munich paper.
The model captures the behavior of the PCM with the Heat Transfer with Phase Change interface. The interface helps predict how these types of materials transform when they change phase. In this case, the researchers determined the temperature transfer in the plaster with Micronal 5038X throughout the simulation.
The exterior temperatures in the model are based on measured temperatures averaged per hour. Using real temperatures increases the accuracy of the simulation, providing a more realistic look at the thermal performance of the PCM in a specific climate.
Note that you can access meteorological data for over 6000 different areas in COMSOL Multiphysics. To learn how, check out this blog post on thermal modeling of the airflow in and around a house.
Analyzing the Results for the PCM-Enhanced Plaster
Let’s look at how the simulation results compare with experimental data. As we can see below, the temperature peaks and timing for the reference plaster and plaster with 5% PCM both show good agreement. Based on these results, the plasters that include 10% and 20% PCM can also be verified.
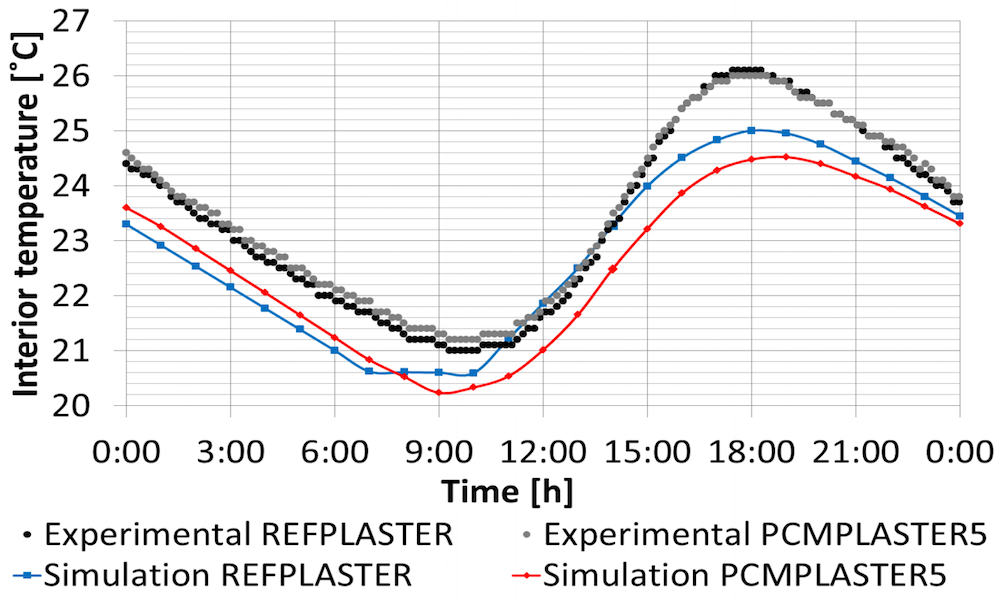
Comparison of the simulation and experimental results for the reference plaster and plaster with 5% PCM. Image courtesy A. Kylili, M. Theodoridou, I. Ioannou, and P.A. Fokaides and taken from their COMSOL Conference 2016 Munich paper.
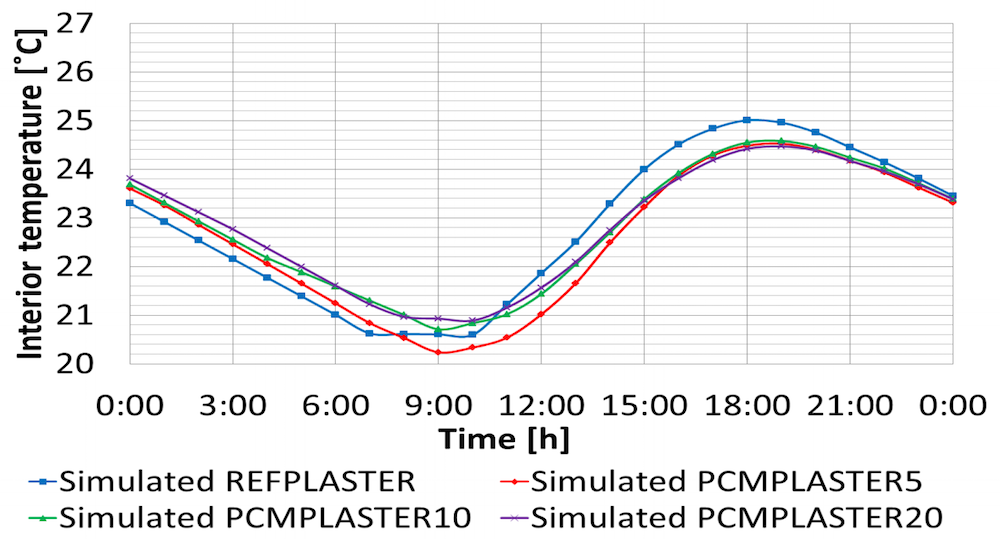
When looking at the thermal performance of the different plasters, we can see that the higher percentage of PCM in the plaster, the better. Using Micronal 5038X minimizes the temperature variation inside a building over a 24-hour time period. Further, it takes longer for the building to reach its maximum and minimum temperatures.
Another useful aspect of the PCM is that it can adjust to different daytime and nighttime temperatures. In 24 hours, the PCM is able to change phase twice.
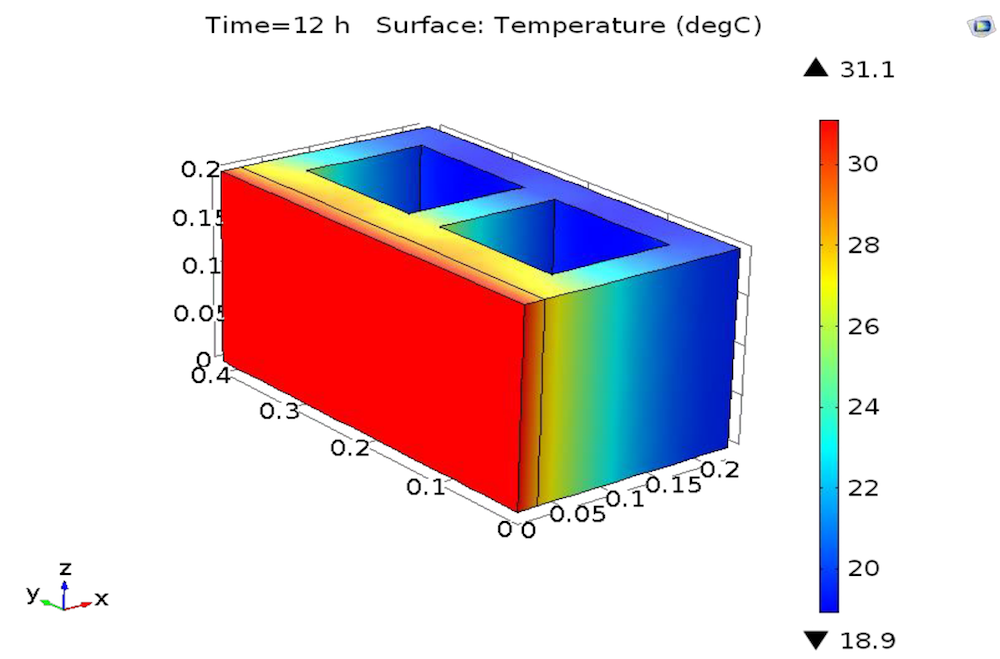
Left: The thermal performance of plasters containing different percentages of PCM. Right: The temperature distribution in a building element that uses a PCM-enhanced plaster. Images courtesy A. Kylili, M. Theodoridou, I. Ioannou, and P.A. Fokaides and taken from their COMSOL Conference 2016 Munich presentation.
Based on the researchers’ simulation results, validated with experimental data, the novel PCM-enhanced plaster can be optimized for use in buildings located in hot climates.
Learn More About Simulating Phase Change Materials
- Read the researchers’ full paper: Numerical Heat Transfer Analysis of a Phase Change Material (PCM) – Enhanced Plaster
- Check out these blog posts on how to model phase change:




Comments (1)
Sunku Prasad J
December 27, 2019Dear COMSOL,
In the apparent heat capacity method, COMSOL is using the following equation for the density of the phase change material:
rho = theta*rho_phase1+(1-theta)*rho_phase2.
we know theta is a function of temperature.
If the density changes with the temperature, how the volume changes are accommodated?
How it is possible to change the density of the material without changing the volume (since the mass of the PCM is constant before and after melting)?
Kindly clarify.
Regards
Sunku prasad