Blog Posts Tagged Technical Content
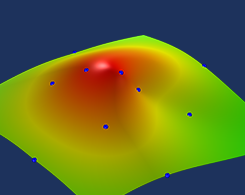
Using Radial Basis Functions for Surface Interpolation
Did you know that you can easily calculate the interpolation between a set of points using a simulation app? Learn more here and download a demo app for design inspiration.
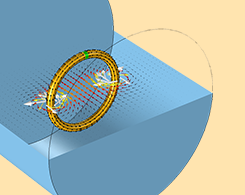
Modeling Coils in the AC/DC Module
A key concept when it comes to coil modeling is closing the current loop. Learn how to do so when modeling coils using the AC/DC Module and COMSOL Multiphysics®.

Generate Models from Text Files with the Application Builder
Ever wish you could automate your model preprocessing tasks? In this blog post, we demonstrate how you can use the Application Builder to quickly convert a text input file into a COMSOL model.
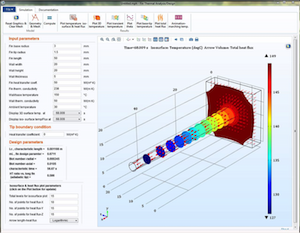
Studying Transient Heat Transfer in a Fin Design with an App
A guest blogger and author presents a simulation app that he designed to study transient heat transfer in a nonprismatic fin.
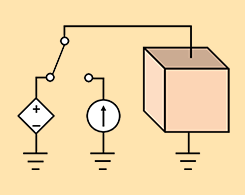
Control Current and Voltage Sources with the AC/DC Module
Did you know that you can use the Terminal boundary condition to dynamically switch between excitation types during a transient simulation? This is useful for modeling power supply, for example.
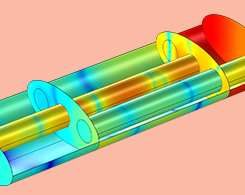
Multiphysics Simulation Provides Accurate Muffler Designs
A guest blogger from Lightness by Design, a COMSOL Certified Consultant, shares how multiphysics simulation provides accurate results when designing automotive mufflers.
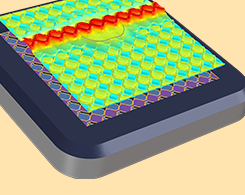
Streamlining Capacitive Touchscreen Design with Apps
In this comprehensive blog post, we discuss the different design considerations for capacitive touchscreens and how simulation apps can be used to streamline their design workflow.
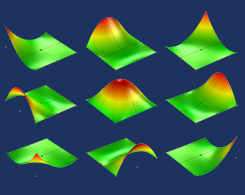
Keeping Track of Element Order in Multiphysics Models
Whenever you are building a finite element model in COMSOL Multiphysics®, it is important that you are aware of the element order that is being used. We demonstrate how to do so here.
