
Today, we will introduce a goal-seeking equation into a model in the COMSOL Multiphysics® software that is used in combination with a fully coupled approach to solving a nonlinear problem. This approach, albeit more computationally expensive than the segregated approach we introduced previously, has some interesting advantages in terms of robustness and highlights one of the core strengths of the COMSOL® software.
Background
As discussed in a previous blog post on introducing goal seeking into the segregated solver, one can augment a multiphysics model with an additional global equation within which we define how to update an input to a model such that a particular output is achieved. This approach takes advantage of the segregated solution approach, solving one part of the problem after another (solving all of the various physics) and then updating the input via the global equation.
Although this approach is very computationally efficient, due to the use of the segregated solver, it relies on an ad hoc update equation that needs to be constructed with some knowledge of the underlying physics of the problem.
Here, we will introduce an alternative approach, wherein the equation for the input is updated based upon an equation that lets the software symbolically compute derivatives. This approach can be much more robust and general, but does come with a computational cost. Let’s first look at how to implement this method, and then address the relative merits.
Here, we will look at the same example we considered before, of a Joule heating problem of two electrodes applied to a medium with an inclusion. The electric and thermal conductivities of the material are nonlinear with temperature. The objective of our model is to adjust the potential difference between the top electrode and the ground electrode such that 3 watts are dissipated within the inclusion.
Using the Fully Coupled Solver to Introduce Goal Seeking
Just like in our previous blog post, this can be achieved via a Global Equation, although this time, we add the Global Equation within the physics that it affects. However, recall that in the former case, this extra equation updates the applied potential using an ad hoc scaling within a separate segregated solver iteration. Here, we will use an equation that contributes terms to the Jacobian matrix when solved simultaneously with the affected physics.
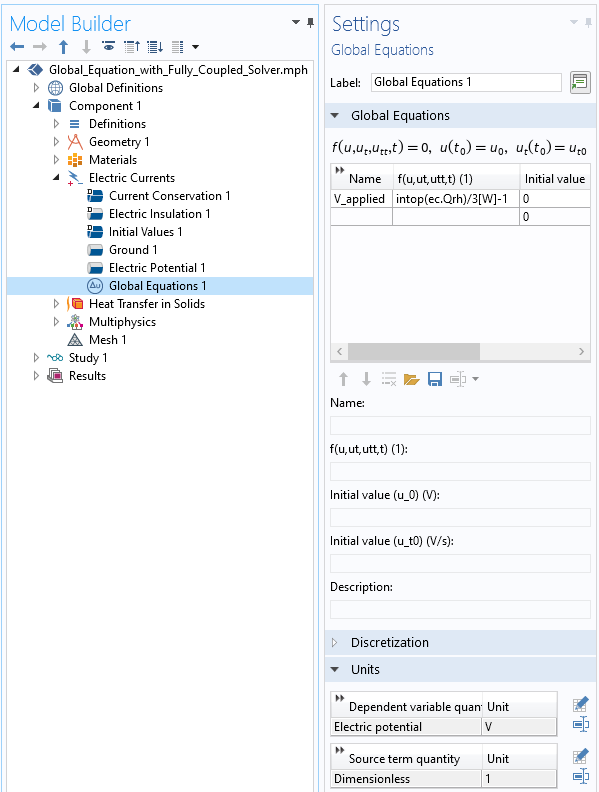
Introducing a Global Equation within a physics interface.
Let’s modify our previous example to demonstrate. We still need to introduce a Global Equation for the applied potential, V_applied, but now we need an equation that is satisfied and solved for at the same time as the equations for the electric potential. To do so, we add a Global Equation feature within the Electric Currents physics. Note that we are entering a residual equation that must equal zero at the solution point. The equation that we enter is:
intop(ec.Qrh)/3[W] – 1
Where intop() is an integration operator defined over the inclusion. We will see later that there are some advantages to the nondimensionalization of this equation. Rearranging, this is equivalent to:
intop(ec.Qrh) = 3[W]
This can be read as: Compute the value of V_applied such that the losses in the inclusion equal 3 watts. We can also write out what this residual equation represents:
When computing the Jacobian contribution, we take the symbolic derivative of this with respect to all of the unknowns in the model. By examination, we can we see that:
whereas the other two derivatives with respect to the electric potential, \partial r / \partial V, and the temperature fields, \partial r / \partial T, will be nonzero.
This means that the global equation introduces a zero on the diagonal of the Jacobian, but many nonzero terms in the corresponding row. This affects the kind of linear system solver that we will have to use within the nonlinear iterations.
It is these additional terms that are the really interesting and useful contribution. These terms tell the nonlinear solver how to update V_applied such that our global equation will equal zero. That is, the software figures out the update to V_applied automatically. (Recall in our previous approach we had to construct our own update equation based upon some knowledge of the physics.)
Introducing Nonzero Gradients
There is, however, a cost to these additional terms. They do require that we simultaneously solve for the global equation and the electric potential equations, and, since they introduce both off-diagonal terms and a zero on the diagonal, they require that the fully coupled approach use a direct linear system solver when solving for the electric potential field and the global equation. In addition, the derivatives shown above have to be nonzero at the initial conditions, otherwise the entire row of the Jacobian would be zero. This turns out to be a bit nontrivial in this case, in that there must be a nonzero gradient in the electric potential at the specified initial values.
There are two ways to introduce a nonzero gradient in the electric potential. The simplest way is to specify a spatially varying initial condition, as shown in the screenshot below, in the Electric Currents physics. This is simple to do, at least in this case, but might not always work, since we do introduce a nonphysical initial value.
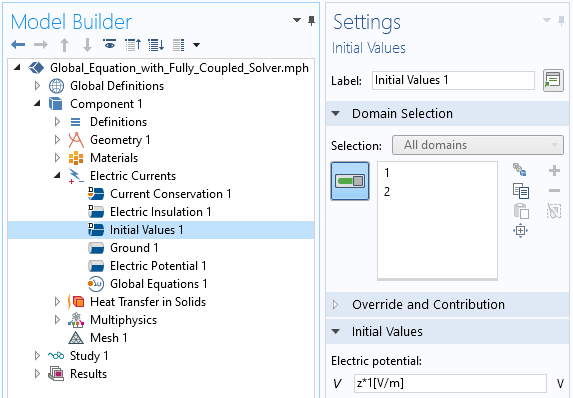
Introducing an initial value into the Electric Currents physics that will lead to a nonzero gradient on the electric potential field.
A more elegant approach is to introduce a variation of our Global Equation for V_applied that solves the equation:
V_applied/1[V] – 1
This equation simply sets V_applied equal to 1[V], and the software will then solve the system of equations and compute a consistent electric potential field. Note that this is why it is helpful to have a nondimensionalized residual equation. This is shown in the screenshot below.
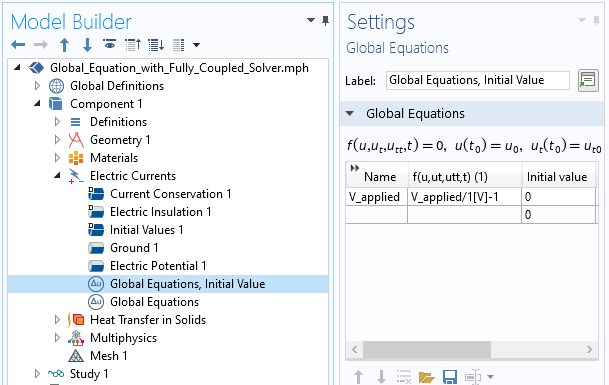
Introducing an additional Global Equation to find an initial value.
Adjusting Solver Settings for the Global Equation
Once we solve for this fixed value of V_applied, the solution to this problem can be used as the initial value once we switch back to using our original Global Equation. This can be achieved via the Modify model configuration for study step check box and then enabling/disabling the two different Global Equations within the two study steps. That is, within the first study step, we simply specify V_applied, and in the second step, V_applied is solved for such that there is the desired dissipation within the inclusion. This is shown in the screenshot below.
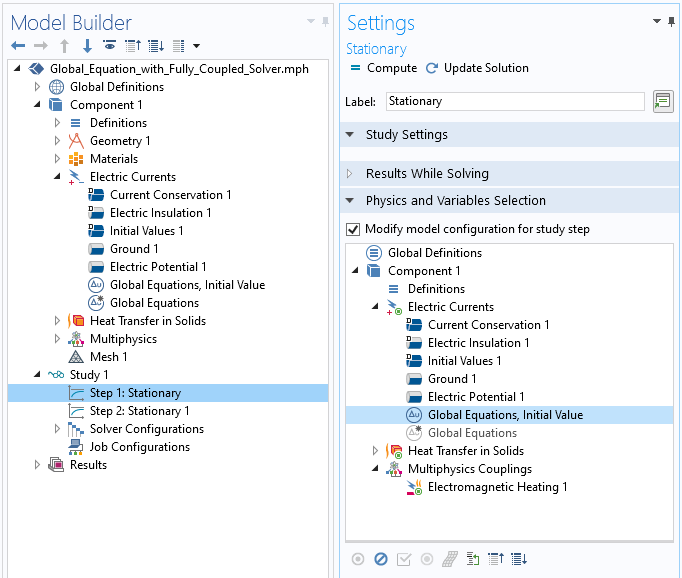
Modifying the model configuration for the first study step, where the Global Equation for the initial value is solved. In the second step, the opposite settings are applied.
This second step does require an adjustment to the default solver settings. There are two choices:
- Use a fully coupled approach for the entire problem, and use a direct solver. This requires the least changes to the solver settings, but solving a large system of equations with a direct solver is going to require a lot of memory.
- Use a segregated solver, but combine the global equations and the electric potential equations into one step, which is solved to convergence using the automatic Newton approach and a direct solver. The temperature solution can still be solved in a segregated fashion using an iterative solver. This approach requires more changes to the settings, but will require less memory to solve. Note that this segregation will lead to the \partial r / \partial T terms being ignored (if they exist at all), which might sometimes negatively affect convergence. These changes to the settings are shown in the screenshot below.
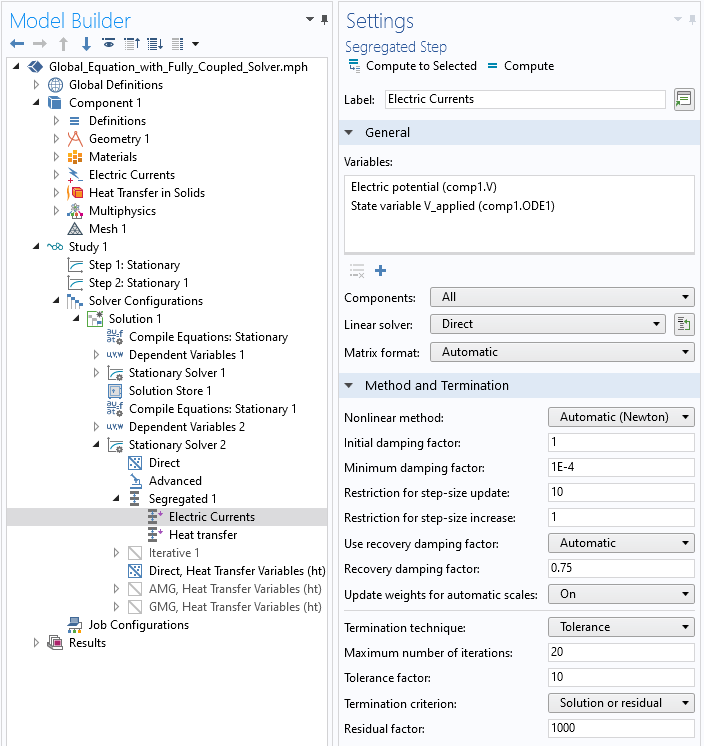
The global equation and the electric potential must be solved simultaneously and using a direct solver.
It is suggested to start with the first approach and try the second if the memory requirements are too high. Note that for 3D models, the memory requirements of the direct solvers go up very quickly with problem size, which is the primary limitation.
Concluding Thoughts
The approach shown here is one of several approaches that can be used to address goal-seeking problems within the GUI without having to resort to any programming. Other approaches for solving this class of problems, discussed in our previous post, are:
- Using the Optimization Module
- Using a parametric sweep and manually identifying the approximate target value
- Augmenting the segregated solver with an additional update equation
The significant advantage of the approach shown here, despite its higher memory requirements, is that it converges quickly and robustly. Note that this technique can also be using in the time domain, as long as the global equation can be satisfied at each time step.
This robust and rapid convergence is a consequence of the additional terms within the Jacobian matrix and highlights another one the strengths of COMSOL Multiphysics for solving highly nonlinear coupled multiphysics problems. This technique, along with the ones discussed previously, are great tools for an analyst to have in their toolbelt.



Comments (3)
Ivar KJELBERG
January 23, 2021Hi Walter,
Thanks for the update Walter, indeed I have been using Global equations in COMSOL for now a couple of decencies, but never really got into he details of the solvers, and as I read you, there are several subtle options to improve convergence, and probably precision.
More for me to play with in the coming days 🙂
Globally I’ll say that you should probably propose more COMSOL training courses on the “solver settings”, for such sets of particular cases, since these are really the strength of COMSOL’s multiphysics approach 🙂
Unfortunately, I see many of my colleague engineers that are using COMSOL as a “classical” click and solve tool, and not using the advantages of the global approach you propose.
Olivier Louisnard
March 19, 2024HI Walter,
Thank you for this interesting blog and the precedent one.
I’ve just realized reading you that I have been using Global equations in a similar way as in the present post for years, to impose current rather than voltage to the terminals of an ultrasonic transducer (avoiding this way ACDC module): an integrating operator computes current I entering through a piezo surface, and I define the voltage Vapp to apply on this terminal so as to get I = Irequired through a global equation. This works perfectly.
What I’m not sure to catch is why in my case, it worked directly without the need to add a second Global equation node and chaining two simulations as you do.
And by the way, I tried to transpose my method to other similar problems without success… Simulation runs without complaining but does not satisfy the global equation. Can’t understand why.
I have still to learn on the topic, I realize…
Thank you again.
Walter Frei
March 19, 2024 COMSOL EmployeeHi Olivier,
You have to be a little bit careful with that approach, it is not *exactly* the same as what the Terminal does. The Terminal is going to be less sensitive to mesh refinement at the boundary. It might be good to compare approaches.