
Modeling the propagation of waves from a large vibrating structure can be a challenging task. It requires balancing the reduction of the computational domain’s size with the decrease of reflection at surface boundaries. With the low-reflecting boundary conditions in the COMSOL Multiphysics® software, we can easily reduce our computational domain to a practical size while ensuring accurate simulation results. Today, we illustrate this with the example of modeling wave propagation in rocks under blast loads.
Studying Wave Propagation in Rocks Under Blast Loads
Across the world, tunnels provide improved modes of transit for those traveling via roads, rails, canals, and even by foot. To construct these underground passageways, blasting technology is often used as a means of fracturing rocks for excavation.

The Lærdal Tunnel, the world’s longest road tunnel, was built with the help of blasting. Image by Svein-Magne Tunli — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
When rocks undergo blasting, they are subjected to loads at the points where holes have been drilled. Understanding how waves propagate within these structures during blasting is key to ensuring this operation’s safety and reliability.
As in other cases that involve modeling the propagation of waves from a large vibrating structure, this can be a challenge. We not only have to deal with a computational domain that is quite significant in size, but we also have to make sure that reflections from the surface boundaries don’t affect the accuracy of the results. In COMSOL Multiphysics, there is a simple solution: using low-reflecting boundary conditions to truncate the computational domain.
To get a better idea of when to use this functionality, let’s look at an example from the Application Gallery.
Using Low-Reflecting Boundary Conditions to Model Wave Propagation
By default, low-reflecting boundary conditions use material data from the neighboring domain to develop a perfect impedance match for pressure and shear waves. Such an approach is best suited for those situations where the wave direction is close to normal at the wall.
In our example, we use a block model geometry. Of the model’s four side walls, two are symmetry planes. The other sides represent truncating the computational domain in the directions where the rock features lateral dimensions much larger than the depth. The size of the block as well as its material parameters correspond to those used in Ref. 1 in the model documentation.
The model geometry and mesh. Note that the two side walls shown are symmetry planes. The blast occurs where the two planes meet at the bottom surface.
The properties of the elastic material applied are shown in the table below. Note that these values correlate with those of a granite rock.
| Material Parameter | Value |
|---|---|
| Young’s modulus | E = 50 GPa |
| Poisson’s ratio | v = 2/7 |
| Density | 2700 kg/m3 |
The top surface of the rock is free, while a load — in this case, a finite duration pressure pulse — is applied to the bottom surface. The load represents an explosion inside the rock close to its surface.
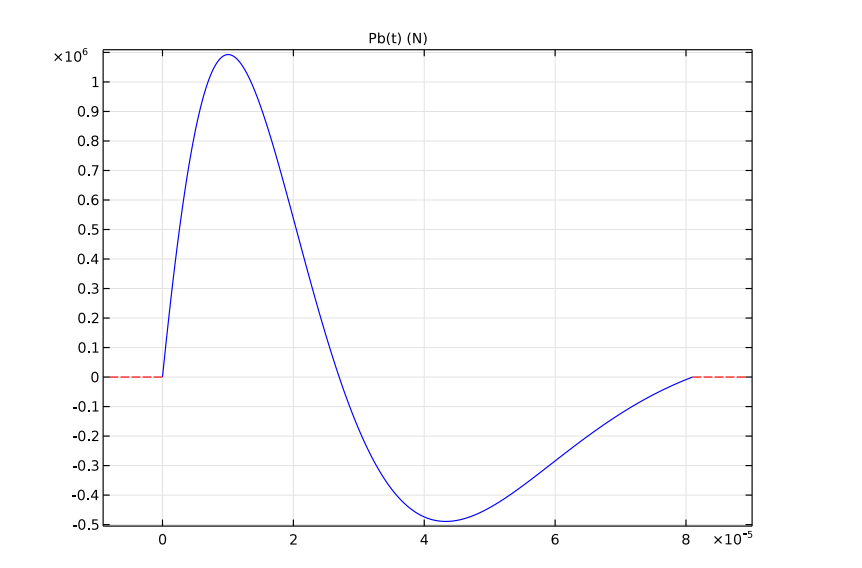
The load function.
For the transient study of the wave propagation in the block, we use a time interval of 150 ms. The following simulation plot depicts the typical pattern of wave propagation.
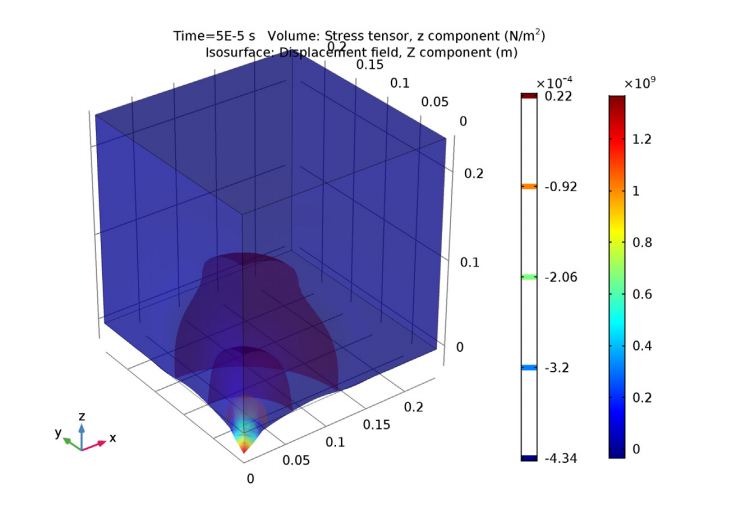
The stress within the block at an early stage of the elastic wave propagation.
Next, we compare the vertical displacement at the upper surface of the rock when low-reflecting boundary conditions are applied (solid blue line) and when they are not (dotted green line). Note that the first and second dashed vertical lines in the plot below represent the analytical estimates for when the incoming and reflected pressure waves reach the surface, respectively. Both of these estimates agree very well with the obtained simulation results. Further, as the plot indicates, the two responses begin to deviate from one another after the estimated time, a result of the reflected wave.
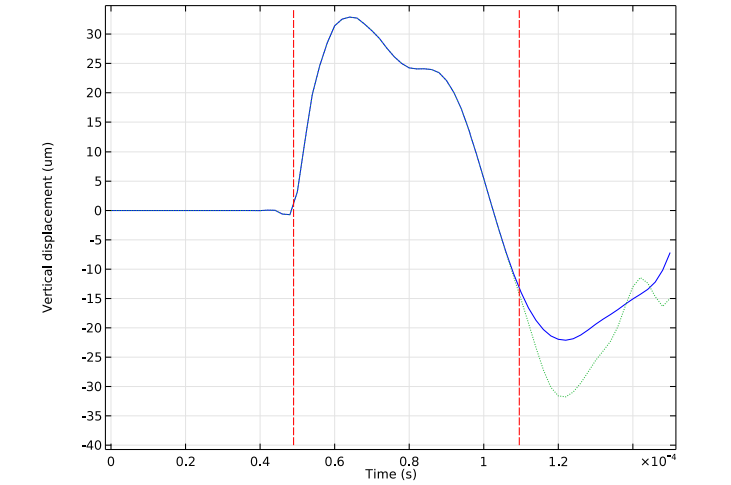
Comparison of the vertical displacement at the rock’s upper surface with and without the use of low-reflecting boundary conditions.
The example presented here is just one of many cases where using low-reflecting boundary conditions can benefit our modeling processes. In addition, this tutorial model can act as a guide for optimizing other simulation studies.
Learn More About Modeling Wave Propagation with COMSOL Multiphysics®
- To see more examples of modeling wave propagation, check out these tutorials:




Comments (0)