
The trebuchet is a large siege weapon that you might recognize from movies set in the Middle Ages or fantasy worlds. This weapon is built on the idea of converting potential energy into kinetic energy to hurl a projectile over a large distance. Simple as it seems, the trebuchet is a complicated dynamical system. In this blog post, we will build a simplified model of a counterweight trebuchet using the Multibody Dynamics Module and examine some of its design features.
War Wolf: The Ultimate Siege Weapon
A trebuchet is a long-range weapon that uses a swinging arm to send a projectile toward a target. The machine is generally associated with hurling boulders at a castle wall to bring it down, but trebuchets have also been used to throw Greek fire and wreak all kinds of havoc. Trebuchets have appeared in several films and TV shows, such as The Return of the King (2003); Marco Polo (2014–2016); and even in Monty Python and the Holy Grail (1975), where a cow was catapulted from inside the castle walls toward an unsuspecting King Arthur!
One nonfictional and historically notable trebuchet is War Wolf (known to the English soldiers at the time as “Ludgar”). In 1304, on one of his campaigns to defeat Scotland, King Edward I besieged Stirling Castle and ordered his engineers to build a giant trebuchet. War Wolf was the largest trebuchet ever made and was rumored to send boulders of about 150 kilograms across a distance of over 200 meters.

A small-scale replica of War Wolf, a counterweight trebuchet that uses a boulder-holding sling at the end of a swinging arm. Image by Ron L. Toms. Licensed under CC BY 3.0, via Wikimedia Commons.
Large trebuchets of this type would typically feature a counterweight roughly ten times the weight of the projectile, which would put War Wolf’s counterweight in the neighborhood of 1.5 tons! The poor prospects of surviving an assault from War Wolf prompted the Scottish garrison inside the castle to offer their surrender. However, the king would not have it, as he was eager to try out his new trebuchet. He forced the Scots to remain inside the castle and restarted his siege. War Wolf proved its worth, and the rest is, as they say, history.
The working principle of a trebuchet is simple. The counterweight is raised and the trebuchet is cocked. When the trebuchet is fired, the counterweight drops, and the potential energy of the system is converted into a combination of kinetic and potential energy. The projectile undergoes a swinging motion and is released at some suitable position along its trajectory. This happens when one end of the sling slips off the tip of the swinging arm.
Performing a Multibody Analysis of a Counterweight Trebuchet
Here, we build a computational model of a basic trebuchet with the Multibody Dynamics Module and version 5.3 of the COMSOL Multiphysics® software.
Our model uses the following assumptions and physical dimensions:
- All of the components are assumed rigid (including the sling)
- All hinged joints are assumed frictionless
- The projectile is prevented from falling through the ground using a penalty stiffness
- The vertical beam of length L5 = 3.5 m, representing the carriage, is fixed
- The ratio of counterweight mass (M = 2000 kg) to projectile mass (m) is 100
- The counterweight hangs from a beam of length L4 = 1 m
- The swinging arm is 6 meters in total length with L1 = 1 m
- The length of the sling is L3 = 3 m
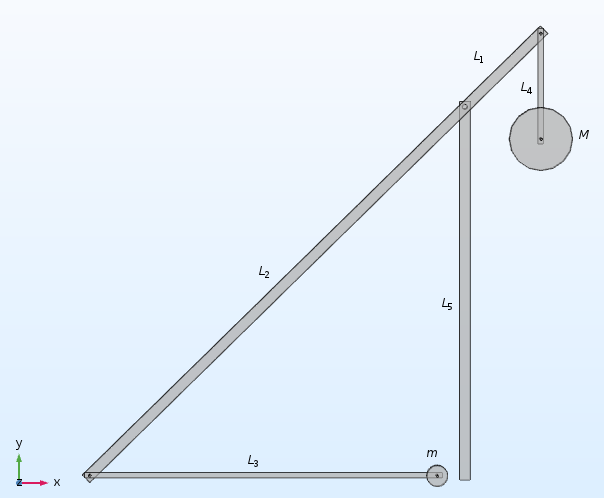
A schematic of the counterweight trebuchet model.
As the projectile is swung around by the swinging arm, it describes a nontrivial motion of varying velocity. If the trebuchet is to be designed for maximum throwing distance, a question arises: At what point during its trajectory should the projectile be released? Elementary mechanics tells us that if we neglect air resistance and the height from the ground at which the projectile is released, the throwing distance s of the projectile (measured in the positive x direction) can be expressed as
where v0 and α are the velocity and angle at the time of projectile release, respectively, and g is the gravitational acceleration.
Thus, finding the maximum throwing distance is equivalent to finding the combination of v0 and α that maximizes s. Intuitively, you might think that the angle of release should be α = 45°. Let’s see if this holds true for the trebuchet model.
The animation below shows the motion of the trebuchet as it is fired. The quantity s is shown along the projectile trajectory, and it represents the throwing distance that would follow from releasing the projectile at a certain point on this trajectory.
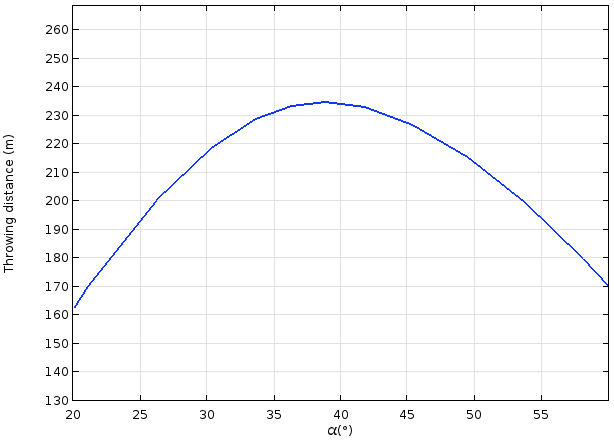
In the results below, the throwing distance is plotted as a function of the release angle α. The maximum throwing distance is obtained if the projectile is released at α ≈ 38°. The plot reveals that deviations of the order of 5° from this optimum only affect the throwing distance by a few meters. In other words, as long as the release angle is roughly correct, the trebuchet will function as intended.
Now, let’s examine what happens if we modify the length of the sling by ±10% using a parametric sweep. The plot below shows that the maximum throwing distance that can be obtained is greatly affected by the length of the sling. So, if you are in the business of designing trebuchets for medieval kings, you should pay attention to this design parameter.
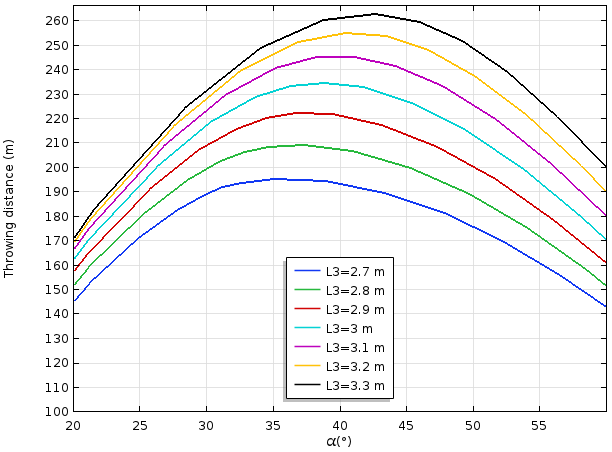
Using a parametric sweep, you could easily examine the effect of changing other physical lengths in the model (while keeping the counterweight at fixed height for consistency). Try for yourself by downloading the model file from our Application Gallery.
Concluding Remarks
In this blog post, we demonstrated that the Multibody Dynamics Module can be used to build a simple model of a counterweight trebuchet. If you are interested in learning more about multibody dynamics modeling, check out these additional blog posts:
- An Introduction to Gear Modeling in COMSOL Multiphysics
- Modeling the Dynamics of a Gyroscope
- The Motions and Mechanics of a Truck-Mounted Crane
Wondering why War Wolf was also called Ludgar? Apparently, the French name Loup de Guerre (“wolf of war”) proved more than a mouthful for the English soldiers, so it was condensed into “Ludgar”.







Comments (0)