If you’ve ever worked with the Terminal boundary condition in COMSOL Multiphysics, you know that this electrical boundary condition can apply a current or voltage, among other options. But did you know that you can also dynamically switch between excitation types during a transient simulation? This is useful if you are trying to model a current- or voltage-limited power supply, for example. Today, we will look at how to implement such a switching behavior.
The Terminal Boundary Condition
When using either the AC/DC Module, the MEMS Module, or the Plasma Module, the Terminal condition can be applied to the boundaries of any domains through which conduction or displacement currents can flow. With this boundary condition, it is possible to apply a Current, Voltage, or Power excitation as well as a connection to an externally defined Circuit or a Terminated connection with known impedance.
Regardless of the type of excitation or the physics interface being used, the Terminal condition always specifies the voltage, but optionally adds more equations to the model. For example, when using a Terminal condition with a specified current, the software automatically adds an Integration Component Coupling feature to integrate the total current through the specified boundary. The software also adds a Global Equation that introduces one additional degree of freedom to the model for the terminal voltage, such that the current through the terminal equals the user-specified current.
This combination of Global Equations with an Integration Component Coupling is quite flexible and you may already be familiar with its usage for structural mechanics and heat transfer modeling. Let’s now see how we can easily switch between different terminal types.
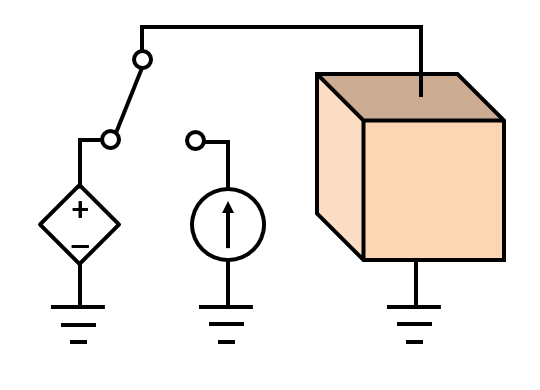
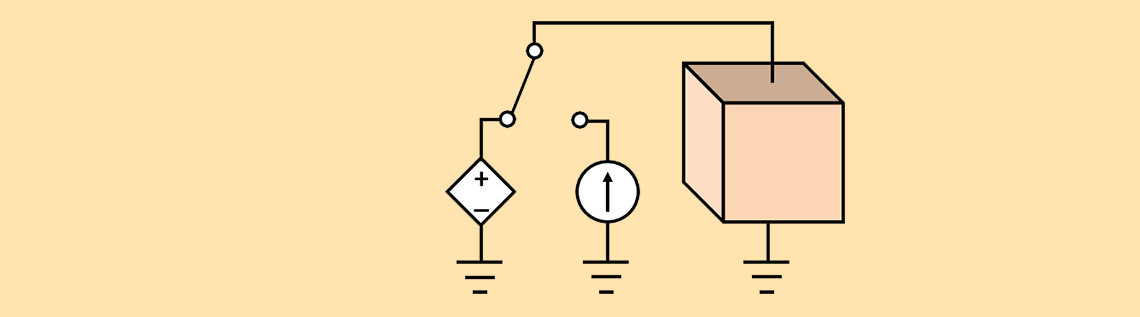
A schematic of a block of material with a ground and a Terminal condition on opposite sides. The Terminal boundary condition will be switched between a voltage or a current source.
Controlling Current or Voltage with a Single Boundary Condition
We will look at a very simple electric current model involving just a block of material with a grounded boundary on one side and a current-type Terminal boundary condition on the other. We will start by considering the steady-state case and address how to apply a current or voltage excitation by adding a Global Equation. The Global Equation itself is added to the Electric Currents interface (To add Global Equations to a physics interface, make sure to toggle on Advanced Physics Options underneath the Show menu in the Model Builder.)
First, we take a look at the Terminal settings. As we can see from the screenshot below, the Terminal type is Current, and the applied current is the variable Current, which will be solved for via the Global Equation.
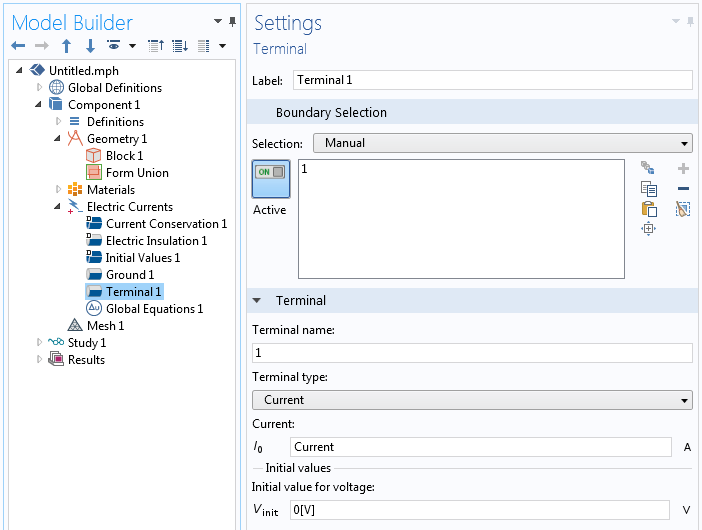
The current-type Terminal condition with an applied current, which will be controlled by the Global Equation.
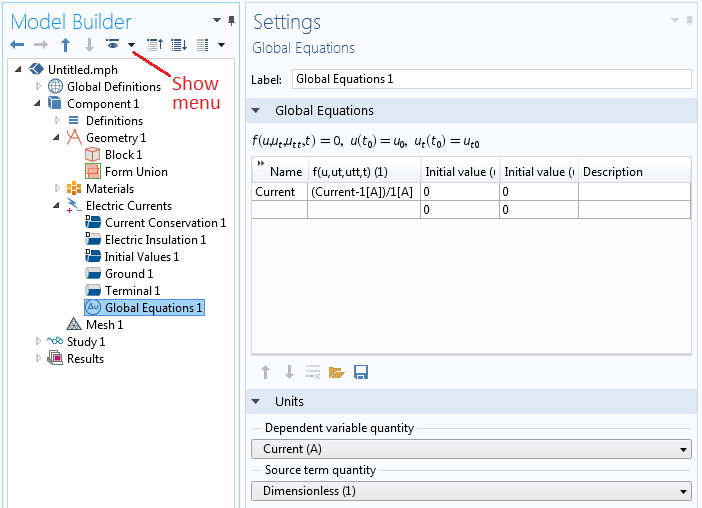
The Global Equations settings control the applied current for the Terminal condition.
The settings for the Global Equation are shown in the screenshot above. There is a single equation for the variable Current, and the equation that must be satisfied is
(Current-1[A])/1[A]
Since this equation, by definition, must equal zero, the applied current equals 1 Amp. This is a straightforward equation; it does not include any feedback from the model, but rather sets the value of Current. The Global Equation itself is nondimensionalized, since we will also want to satisfy an equation for voltage. Switching to a voltage excitation can be done by simply changing this equation to
(ec.V0_1-3[V])/3[V]
where the variable ec.V0_1 is automatically defined by the Terminal boundary condition.
We are thus applying a current such that the terminal voltage is equal to 3 Volts. This equation does introduce a feedback from the model, but the model is still linear. It will still solve in a single iteration, but it does require using a direct solver. If you try this out yourself, you can see that you can now switch between a voltage and a current excitation simply by changing the Global Equation for a stationary problem. Next, we will look at how you can dynamically switch between these excitations during a transient simulation.
Switching the Global Equation During a Time-Dependent Simulation
Let’s suppose that we have a power source driving a system that exhibits variable resistance. For example, resistance changes with temperature due to Joule heating and induction heating. Let’s also suppose that, as the resistance changes, our power source can supply a constant current up to some peak voltage, or a constant voltage up to some peak current.
To model this type of switch, we will use the Events interface. We have previously written about the Events interface for implementing a thermostat for a thermal problem and we recommend reviewing that blog post for technical details and relevant solver settings.
The Events interface contains four features: a Discrete States feature, an Indicator States feature, and two Implicit Events features. First, the Discrete States feature defines a single-state variable, CC, which acts as a flag indicating if the power supply is in constant-current mode, CC=1, or constant-voltage mode, CC=0. Initially, our power supply will be in constant-current mode. Next, there is an Indicator States feature defining two indicator-state variables, PeakV and PeakI, which should vary smoothly over time. Lastly, there are two Implicit Events features, which will track these two indicator-state variables and change the discrete-state variable, CC, to zero or one if the logical conditions are met. These settings are all shown in the screenshots below.
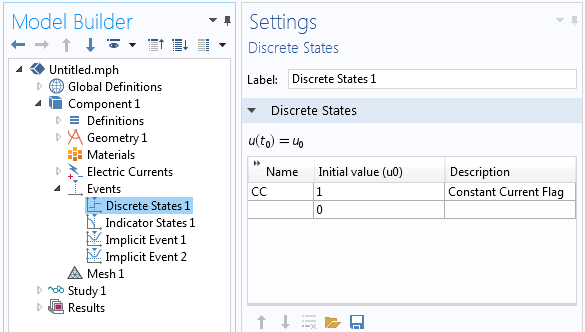
The Discrete States feature defines a flag that signals the Terminal state.
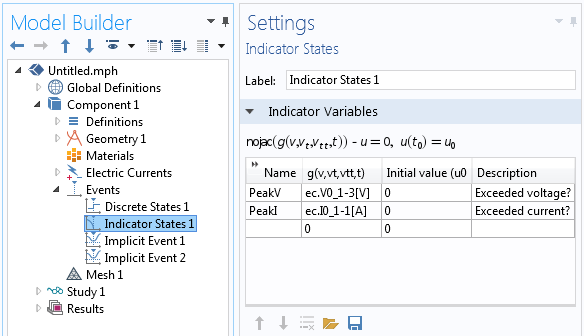
The Indicator States feature defines two different possible events indicators.
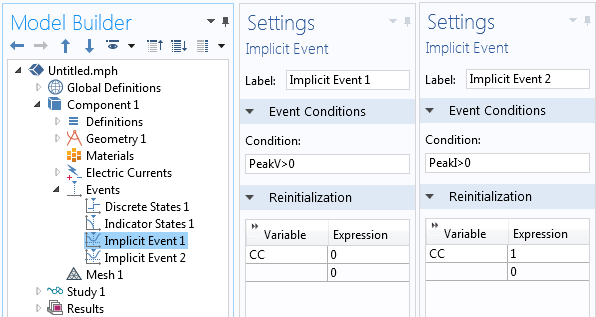
The Implicit Events toggle the Discrete States variable.
There is only one task left to do: modify the global equation for the variable Current to be
CC*((Current-1[A])/1[A])+(1-CC)*(ec.V0_1-3[V])/3[V]
You can see that this is a sum of the two expressions developed earlier for either current control or voltage control using the CC flag to switch between them. Once this is done, it is only a matter of solving in the time domain with the study settings described in our earlier blog post and using a direct solver for the Electric Currents voltage field, the Terminal voltage, and the Global Equation for the current, as shown in the screenshot below. The Events variables can be solved in a separate segregated step.
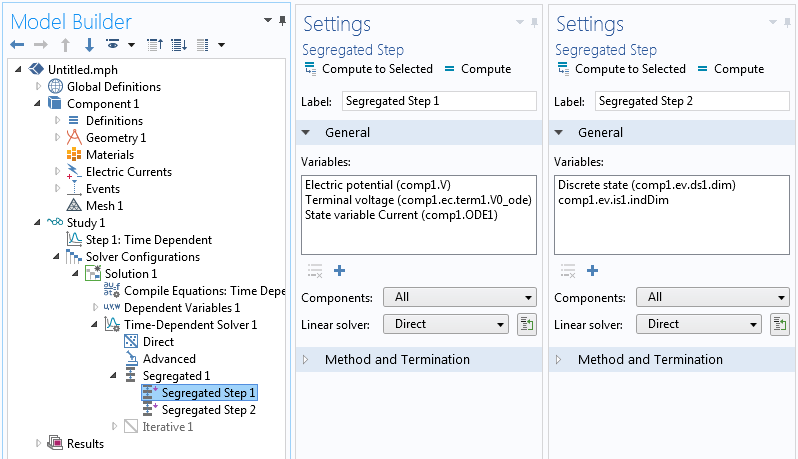
Solver settings showing how the variables are segregated and that a direct solver is being used.
With these features, we have now implemented the following power supply behavior:
- Initially, apply a constant current of 1 Amp and adjust the applied voltage to maintain this current.
- If the voltage exceeds 3 Volts, switch over to constant-voltage mode.
- If the current exceeds 1 Amp, switch back over to constant-current mode.
To generate some representative results, we will explicitly make the total resistance of our domain vary over time, as shown in the plot below. We can see from the subsequent plots of current and voltage that the supplied current is initially constant but the voltage rises due to increased resistance. The power supply then switches over to constant-voltage mode and the current varies. As the resistance goes back down, the current rises to its peak and then the power supply switches back to fixed-current mode.
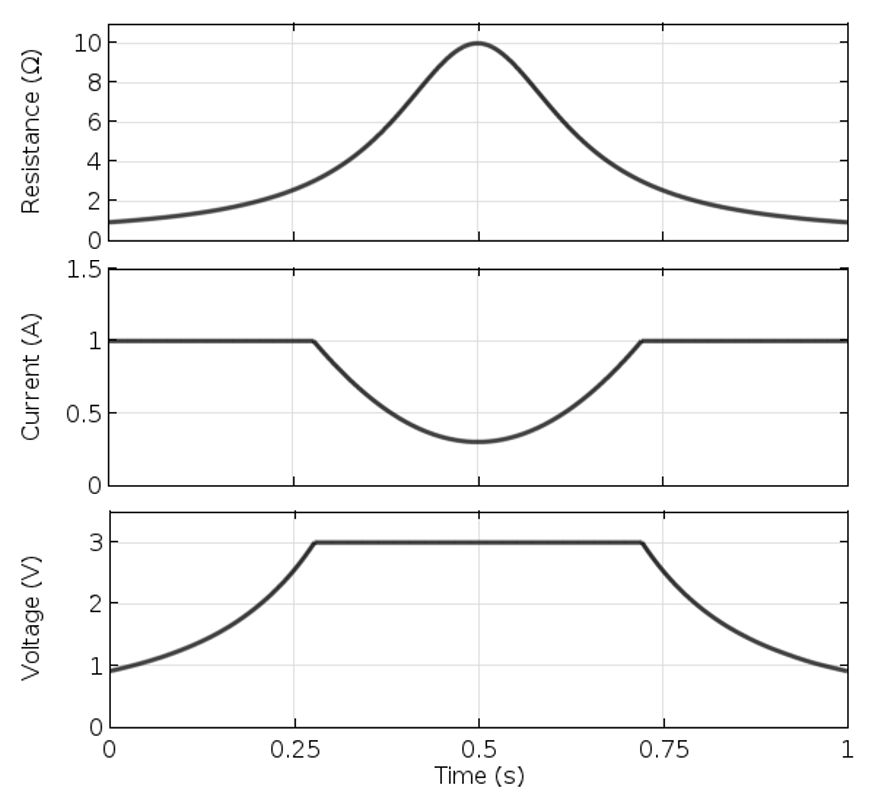
As the device resistance varies over time, the source switches between constant current and constant voltage to ensure that the maximum current and voltage are never exceeded.
Closing Remarks on Using the AC/DC Module to Control Current and Voltage Sources
We have demonstrated a control scheme that enforces both a current and voltage maximum, implemented with Global Equations and the Terminal boundary condition. The functionality of the Terminal boundary condition used here is not limited to the Electric Currents interfaces. The Terminal condition is also available within the Magnetic and Electric Fields interface as well as the Magnetic Fields interface, where it is called the Boundary Feed or Gap Feed condition. The Magnetic Fields interface also includes a Multi-Turn Coil domain feature that can be used equivalently.
It is also possible to use this type of control scheme during a Frequency-Transient study, which often occurs in Joule or induction heating, wherein the electromagnetic problem is solved in the frequency domain and the thermal problem, which solves for the temperature variations that lead to impedance changes, is solved in the time domain. This can be particularly useful in the modeling of, for example, RF heating and ablation.
The Battery Design Module, Corrosion Module, Electrochemistry Module, and Electrodeposition Module all contain the Electrode Current and Electrolyte Current boundary conditions that can be used equivalently to the Terminal condition demonstrated here. In particular, the Capacity Fade of a Lithium-Ion Battery tutorial model shows how to model the charging and discharging of a battery.
We hope you can see that with a little bit of imagination, it is possible to implement some quite complex control schemes with the Terminal boundary condition and the Events interface.
If you have a particular application that you’d like to model with COMSOL Multiphysics, please don’t hesitate to contact us.



Comments (8)
M.A.
December 14, 2016This is a great tool, thank you for the post. However, I need to create a similar switch between current/voltage modes in frequency domain, and I am having problems triggering the events to switch the value of CC at different frequencies. Can you help with a similar simple example?
Let’s say we have a simple electric circuit with a resistor, inductor, and a current source. I can create similar global equations and events. I want to switch from current mode at low frequencies, to voltage mode at higher ones. However only the initial value of CC controls the rest of the run in frequency domain. How can I make the simulation check and change the indicator state for every frequency?
Walter Frei
December 14, 2016 COMSOL EmployeeHello Majd, The events interface is meant for transient (time-domain) simulations, and wouldn’t be applicable for stationary (frequency-domain) problems. Since a sweep over frequency is equivalent to solve a sequence of stationary problems, the simplest approach will be to simply divide the sweep up into two distinct problems, one for the current-controlled, and one for the voltage-controlled case.
Choi Chan young
August 23, 2018Thank you for your instruction but i have some questions.
Why (current-1)/1 has to be divided by 1 and (voltage-3)/3 has to be divided by 3??
Walter Frei
August 23, 2018 COMSOL EmployeeHello Choi Chan, This is done for scaling purposes. We want the equation for current to have roughly the same magnitude regardless of the current or voltage control case.
shahab Yousafzai
September 13, 2018current and voltage source can be converted into one another. How to convert circuit to voltage source? https://electric-shocks.com/ideal-and-practical-source/
YOUNG SHEN
December 19, 2019Thanks for the explanation, I need to create a similar switch between impedance / mass in the time domain.
Let’s say we have a simple electrical circuit with yours, current sources replaced by impedance and voltage source replaced by ground (piezoelectric module)
Mohd Khairulanwar Bin Mohmad Johar
May 3, 2020Nice sharing. But i have to simulate polarization and depolarization current. What i need to set in comsol tu run the simulation? If you know, can you help me to show the step?
James Matthew
July 14, 2022Great post. Thanks for sharing. I did something similar while simulating the switch but received an error. https://colorviewfinder.co/solar-switch/