
In earlier versions of COMSOL Multiphysics, it was cumbersome to connect 1D pipes to 3D flow domains. However, did you know that a new feature in COMSOL Multiphysics version 5.0 now allows you to easily accomplish this? Let me demonstrate how this feature works.
The Pipe Flow Module
The Pipe Flow Module has been around for quite some time now. My impression is that this add-on to COMSOL Multiphysics is well received by its users. Many of them view it as a natural extension of the CFD Module and the Heat Transfer Module.
The whole idea with the Pipe Flow Module is that fluid flowing in extended piping and channels largely follows the laws for fully developed flow. As such, you don’t need to resolve the complete flow field with volume elements. You can simply make the assumption that the flow is fully developed.
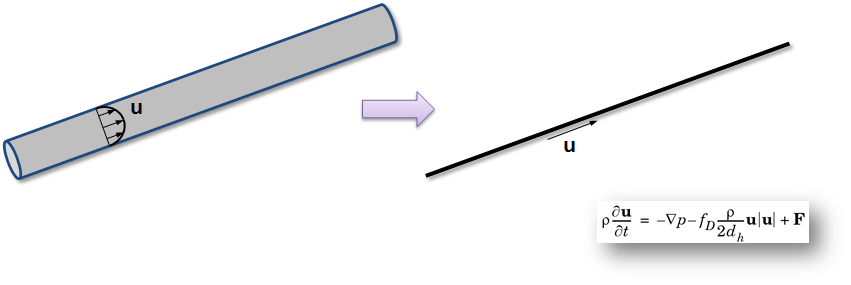
The pipe flow equations (right) only solve for an average velocity and the pipe is only represented by a line in the geometry (middle). This approach saves computational time and cuts memory requirements.
Connecting Pipe Ends to Volume Flow Models
In the image below, pipes are embedded in a solid mold. The heat transfer between the cooling fluid inside the pipes and the mold is studied. In this scenario, however, many users want to connect a pipe section to a 3D fluid flow domain.
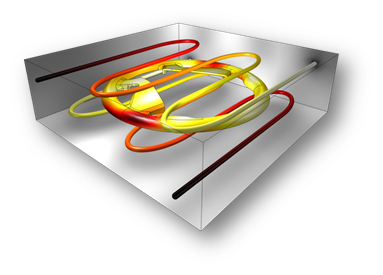
Pipes embedded in a solid mold. Image taken from the Cooling of an Injection Mold model entry.
This is a common occurrence when you have long stretches of slender pipes that suddenly open up to a larger fluid volume that cannot be approximated by a pipe equation.
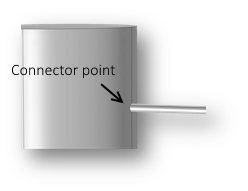
The fluid volume is attached to pipe segment, a 3D curve in the geometry.
The Pipe Connection Feature
In earlier versions of the COMSOL software, this coupling was possible to do. The old process, however, was rather involved, as it required users to set up coupling operators and do a lot of bookkeeping to get it right. In COMSOL Multiphysics version 5.0, we decided to make this easier by providing the Pipe Connection, a feature in the Pipe Flow interface.
This feature couples a 1D pipe segment (modeled with the Pipe Flow interface) with a 3D single-phase flow body. The pipe connection is added as a multiphysics feature and is selected by default on the relevant points in the geometry. This selection can be modified by the user.
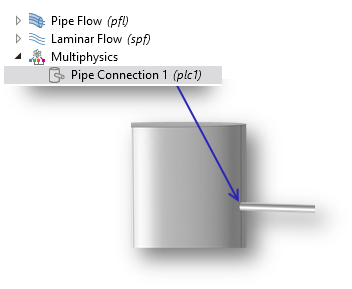
The Pipe Connection feature in COMSOL Multiphysics®.
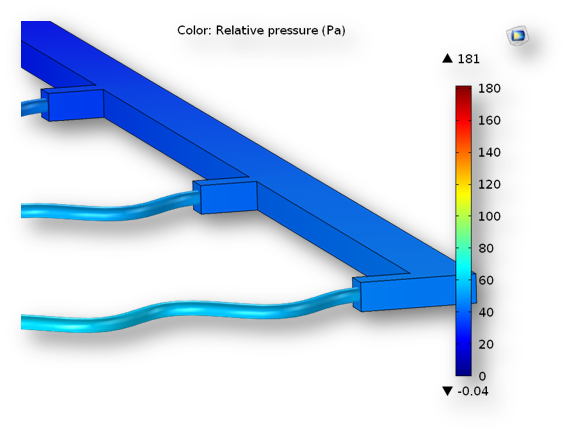
A detailed schematic from the Convective Flow in a Heat Exchanger Plate model. The wavy segments are pipe flow sections and the block-shaped body is a 3D flow domain.
Model Download
- See how easy it is to connect 1D pipes to 3D domains: Download the Convective Flow in a Heat Exchanger Plate model



Comments (7)
Jesus Lucio
February 25, 2018Hi.
Very useful blog, nice presentation, thanks a lot. The ‘Pipe Connection’ feature allows a connection for the fluid part of the model. But what about the ‘Nonisothermal Pipe Flow Interface’? Does it also easily allow a connection for the heat (temperature) part?
Jesus.
Niklas Rom
February 26, 2018 COMSOL EmployeeHi, Jesus the temperature connection is not built in to the Pipe Connection feature yet, but you can couple the temperature manually like in the example below:
Kind regards
Niklas
——————————————-
http://cds.comsol.com/mg/15a93f7c15b093.zip
Estimated size: 11.7 MB
This link expires March 5, 2018. Please make sure to download before that date.
Included files:
– Pipe_CFD_k-eps_test_53a_T.mph
——————————————-
Kensuke Hanada
January 11, 2019Hello,
Now I’m using the version 5.2a, and am trying to connect pipes (Nonisothermal Pipe Flow Interface) to a 3D box (Turbulent Flow(k-ε) Interface). Are there any solutions or examles?
Thank you!
Kensuke
Niklas Rom
January 11, 2019 COMSOL EmployeeHi Kensuke,
the turbulent pipe connection was introduced in the latest version (5.4) of COMSOL Multiphysics. Please download that from https://www.comsol.com/product-download and then you can open the example above and switch to turbulent flow.
If you have any more questions, contact support@comsol.com.
Kensuke Hanada
January 16, 2019Thanks for your prompt reply!
It is of great help!
Artur Kucharewicz
September 26, 2025Is there a related model showing how to connect a 1D nonisothermal pipe flow (nipfl) to a 3D fluid domain in COMSOL 6.3? As far as I can tell, pipe connection is feature that can only be applied to a system where Pipe Flow (pfl) is present rather than nipfl as I would like to do.
If this is not possible via pipe connection, is there a model that instead utilizes the extrusion (linear, general, etc) Definition operations for projecting values from 1D end points to 2D faces?
Niklas Rom
September 28, 2025 COMSOL EmployeeSure Artur. I have sent you an example in email.