Evaluate Characteristics of a Periodic Finned Pipe with an App

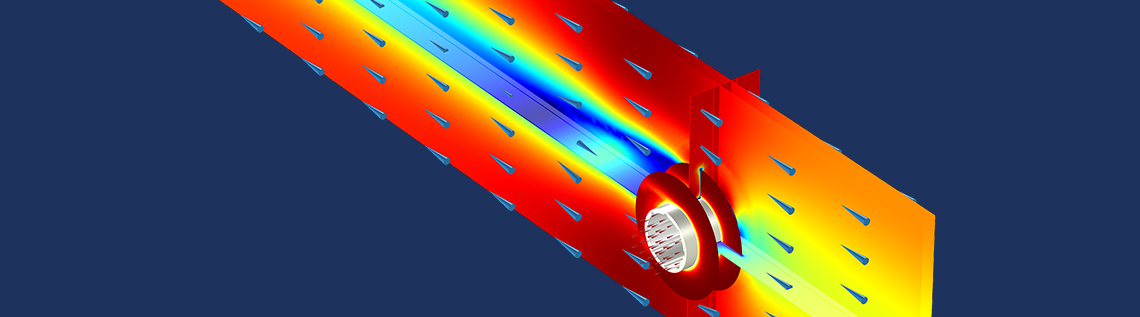
Radiators, refrigerators, and geothermal pumps all need to efficiently extract heat from one fluid to another without mixing them. Among all of the different heat exchanger designs, finned pipes aim to increase the exchange surface between the content of a pipe and the exterior using fins. Finned pipes usually show a geometrical periodicity along the length, which we will take advantage of in this demo app to reduce computational costs.

Modeling a Finned Pipe in COMSOL Multiphysics

Before we delve into our Finned Pipe demo app, let’s explore the physics behind the underlying model. We start by creating the geometry for a simple configuration of a straight pipe separating two fluids at different temperatures. The fins and the periodicity property will be accounted for at a later point.

Finned pipes used in a biomass heat and power plant. Image by Sensenschmied — Own work. Licensed under CC BY 3.0, via Wikimedia Commons.

A straight pipe is placed in the middle of an air domain exhibiting forced convection while water flows inside the pipe. The Conjugate Heat Transfer interface is well-suited for this kind of model, since it:

• Solves the Navier-Stokes equations in the air and water domains
• Solves the heat transfer equation in all domains
• Ensures continuity of the temperature field at the fluid-solid interface

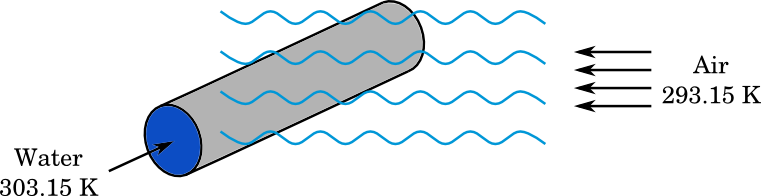
A straight pipe with water flowing inside and forced air convection outside.

Water enters the pipe at a higher temperature than the air that is blown past it through forced convection. The temperature difference between these two inlets is denoted \Delta T. Then, depending on how you see it, water heats up the ambient air or the air cools down the flowing water. In the extreme case, for a sufficiently long pipe, the temperatures of the air and water would eventually reach equilibrium at the pipe outlet. Adding fins enhances heat exchange through the pipe walls and consequently can achieve the same heat transfer rate with a shorter pipe length compared to a pipe without fins.

Calculating the Heat Dissipated Rate per Unit Temperature

The heat dissipated rate per unit temperature and length, h_L, is defined as the ratio of heat rate, \Phi, to pipe length, L, and temperature difference between the two fluids at inlets, \Delta T. In other words, by knowing L and \Delta T, we can retrieve the heat rate exchanged by the two fluids, \Phi, according to:

(1)

For the same pipe length, L, adding more fins would result in enhancing the heat dissipated rate from the hot fluid to the cold fluid, but at the cost of increasing the heat exchange surface and material required for the fins. The heat dissipated rate per unit temperature indicates how well the pipe lets heat energy exchange between its inside and outside regions, with a higher value reflecting more dissipation of the heat exchanger and a more efficient heat exchanger.

Boundary Conditions for the Periodicity Property

Pipes that are a few meters in length typically have a diameter of a few centimeters. Such a large aspect ratio of the geometry often means that a lot of mesh elements are needed for the computation. In finned pipes that show a periodic pattern, such as in the figure below, solving for only one periodic element would considerably reduce computational costs. This requires that the heat transfer properties of the materials are considered independent of temperature and pressure. Then, boundary conditions accounting for the periodicity must be applied.

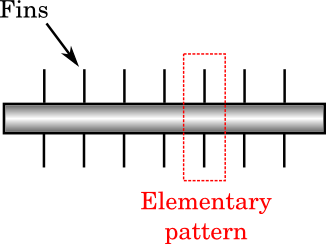
Elementary pattern of a periodic finned pipe.

Let us now work on the simplified geometry consisting of an element of periodicity. The figure below shows the inlet and outlet boundaries, labeled \partial \Omega_\mathrm{inl} and \partial \Omega_\mathrm{out}, respectively. Note that \partial \Omega_\mathrm{inl} is also the outlet of the preceding element of pipe and \partial \Omega_\mathrm{out} is the inlet of the next element.

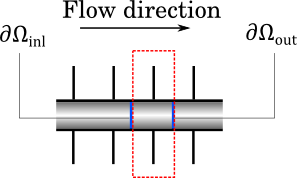
Inlet and outlet boundaries of an element of periodicity.

The geometrical periodicity of the pipe is reflected in the:

• periodicity of the velocity profile
• pseudoperiodicity of the pressure profile with an offset \Delta p_\mathrm{pipe}
• pseudoperiodicity of the temperature profile with an offset \Delta T_\mathrm{pipe}

which are mathematically written as:

(2)

The subscripts \mathrm{inl} and \mathrm{out} indicate whether the quantity is evaluated at the inlet boundary, \partial \Omega_\mathrm{inl}, or at the outlet boundary, \partial \Omega_\mathrm{out}.

For example, the figure below illustrates a pseudoperiodic profile where the offset is found to be 0.003 K. Water entering the pipe element with an average value of 303.15 K exits at 303.147 K.

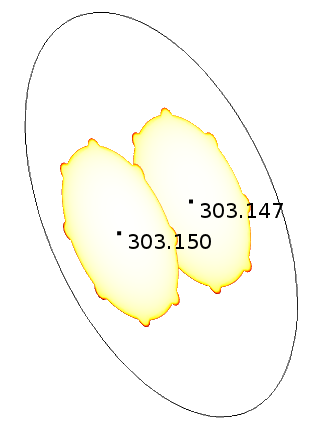
The pseudoperiodic temperature profile between the inlet and outlet of a periodic pipe element, with an offset of 0.003 K.

The temperature offset \Delta T_\mathrm{pipe} is such that \Delta T, the prescribed temperature difference between the water and air inlets, is satisfied.

Characterizing the Finned Pipe

Here, we finally summarize the method to determine the quantities of interest that characterize the heat exchange through the pipe. The temperature dependency of the material properties is negligible so that the flow can be considered incompressible and the simulation can be performed at an arbitrary temperature reference.

In the domains, the equations to solve are:

• The incompressible Navier-Stokes equations for the air and water domains
• The heat transfer equations for all domains

The default boundary conditions describe the situation where:

• Air arrives by forced convection at 293.15 K and a known velocity \mathbf{u}_0
• Water enters the pipe at 10 K higher than air, namely 303.15 K
• Pseudoperiodic boundary conditions for water flowing inside the pipe are those mentioned in (2)

The simulation computes the heat rate, \Phi, transferred from water to air. This determines the heat dissipated rate per unit temperature and length, h_L, according to

(3)

where L is the periodicity length and \Delta T is 10 K.

The pressure and temperature drops are also computed in the Finned Pipe app, which we will discuss next.

Exploring the Finned Pipe Demo App

The Finned Pipe app, found in the Application Gallery, implements the model described above. The app takes care of many of the complexities mentioned above, hiding them behind a user-friendly interface. Knowledge of the physics presented in the above section is not necessary in order to use this app, so you can deploy it to colleagues who don’t have a lot of experience in simulation and the physics of heat exchangers.

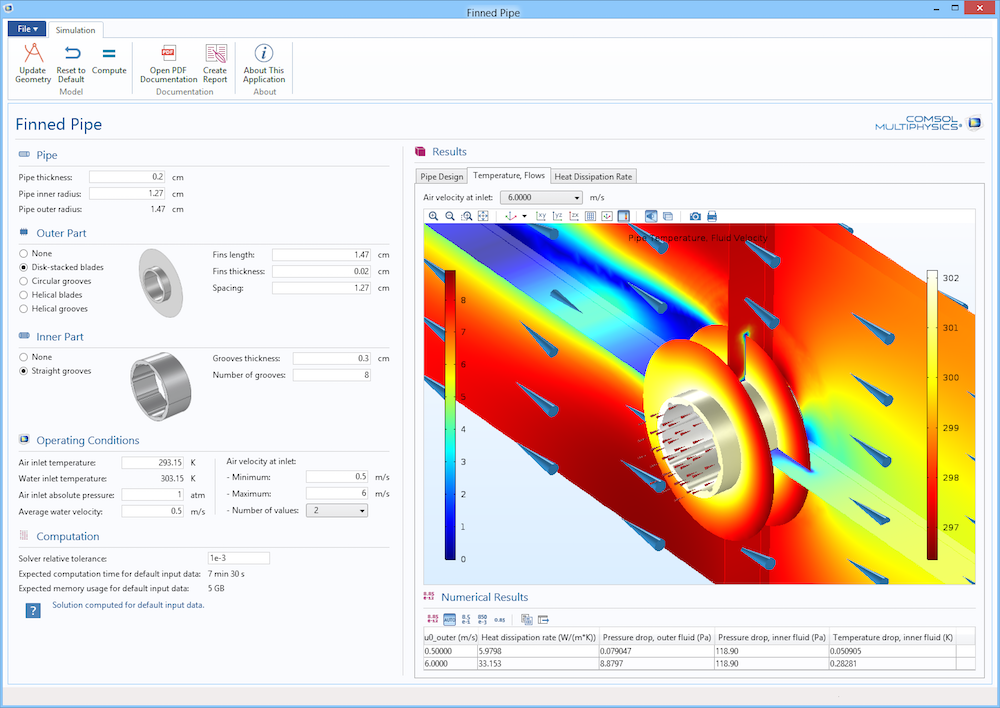
The graphical user interface of the Finned Pipe app.

We start by defining the design of the pipe, selecting among different available shapes. Possible fins added outside of the tube include helical blades and disk-stacked blades. Grooves can be added inside and outside of the pipe to further increase the exchange surface.

A straight pipe, a pipe with helical fins, and a pipe with circular grooves.

The Mass and Dimensions section displays data on the pipe, with the material set as copper and a full pipe length of one meter.

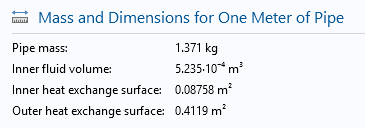
Mass and dimensions for a disk-stacked finned pipe of one meter with straight grooves inside.

Then, we set up the operating conditions by:

• Choosing the air inlet temperature
  • The water temperature is automatically set to 10 K higher than that of the air inlet
• Customizing the absolute air pressure, if necessary
• Customizing the water velocity inside the pipe to adapt to our needs

Since \tilde h may depend on the air velocity blowing outside the pipe, we need to specify the parametric study on this velocity so that the computation presents a curve of \tilde h for different values. The graph below shows the curve of \tilde h obtained for air blowing from 1 m/s to 8 m/s, which reveals a slight incurvation from a linear relation.

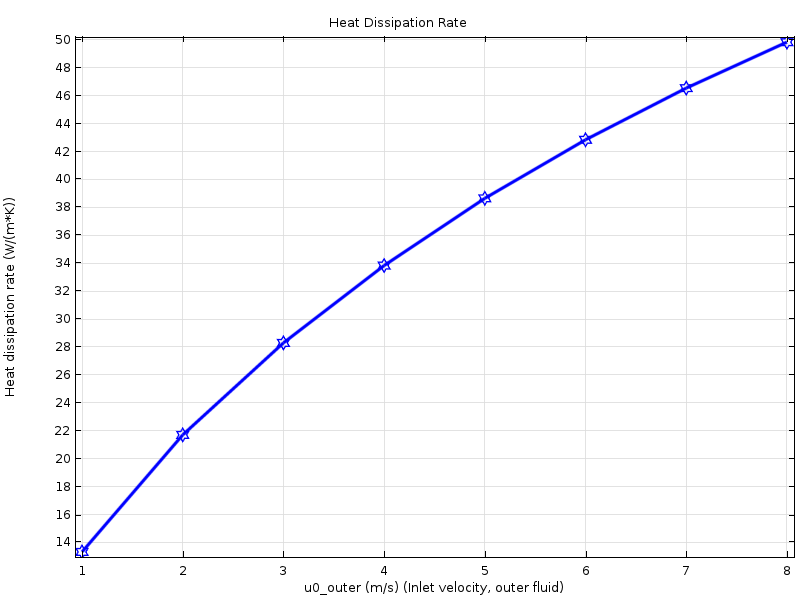
The heat dissipation rate per unit temperature versus air inlet velocity.

Various possibilities are offered in this app by changing dimensions and physical conditions. What will the results be if the periodicity length is less? What about the effects of the fin thickness? Customizing the app provides even greater possibilities, from changing the material to adding more geometries.

Further Explore Simulating Finned Pipes with an App

• Try it yourself: Download the Finned Pipe app
• Read the app documentation for more detailed information
• Watch this archived webinar for a demonstration on how to build and run simulation apps