
Inductive devices exhibit a range of electromagnetic effects that have to be taken into account when they are utilized as part of any application. With the tools provided by the AC/DC Module in COMSOL Multiphysics, you can model and design an inductor in a straightforward yet accurate way, as well as calculate the device characteristics your application demands.
The Basic Physical Principles of an Inductor
An inductor, at its simplest, takes the form of a conducting wire (the winding or coil) wrapped around a chunk of typically magnetic material (the core). Its action depends on the concept of inductance, whereby a magnetic field established around the inductor opposes the change of current flow through the device.
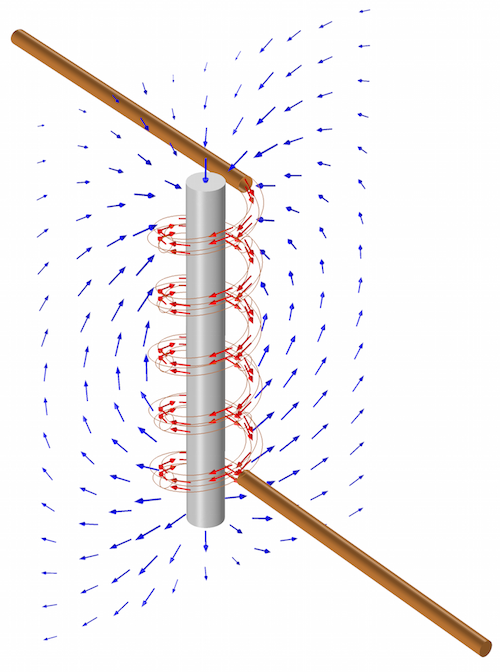
A simple inductor, consisting of a copper winding around an iron core. The red arrows show the current direction and the blue arrows show the magnetic field outside of the core. A change in the current also changes the magnetic flux through the winding, producing a potential across the winding that opposes the change in current.
Inductance is the parameter that measures to what degree a change in current flow is opposed and is usually denoted by L, which would completely characterize an ideal inductor. Unfortunately, we do not inhabit an ideal world and real inductors also display resistive effects (important at low frequencies and characterized by resistance, R) and capacitive effects (important at high frequencies and characterized by capacitance, C), which cause self resonance. In fact, a 3D inductor can often be well understood by an RLC circuit model or some extension thereof.
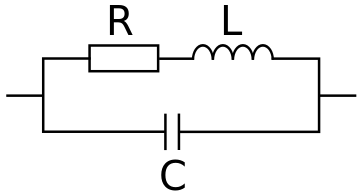
An equivalent circuit that can mimic the behavior of a real inductor.
Alone, or in combination with other circuit elements such as capacitors or resistors, the property of inductance can be applied in all sorts of applications. When used with an alternating current, an inductor alone can function as a low-pass filter or in series with a capacitor as a resonant filter or bandpass filter. Inductors also play important roles in many key parts of daily life, such as switched power supplies and matching circuits connected to RF antennae. A traffic light that conveniently changes as you approach could well be an inductive sensor helping you on your way!
Optimizing an Inductor Design by Characterization
If your device includes an inductor, it is crucial to know some characteristics of the inductor to understand fully how your device functions as a whole. The key parameters include the inductance and may also include the resistance; capacitance; resonant frequency; and the Q factor, the width of the peak around the resonant frequency. These parameters determine such factors as the cutoff frequency or passband for filtering applications, or simply the reactance of a matching circuit.
Another potential concern when using inductors is electromagnetic interference (EMI) or electromagnetic compatibility (EMC). Since inductors set up a magnetic field around their coils, you may need to know what impact this will have on other components or devices close by, especially since modern circuits have become more tightly packed.
Crude analytical or empirical formulae do exist to describe these RLC parameters, but such formulae cannot deliver the high accuracy required for the design of modern devices. This is especially true when the shape of the device deviates from those few shapes that can easily be handled analytically, such as cuboids, cylinders, helices, and tori. The shape and fall-off of the magnetic field around an inductive device for EMI/EMC purposes are less well described.
Additionally, you may want to make the core of the inductor from a nonlinear magnetic material to increase the inductance and limit the surrounding magnetic field. This would add yet another layer of complexity to the calculations, hence another layer of analytical or empirical approximation, casting more doubt on the result. In order to obtain a truly accurate characterization of a three-dimensional inductor device, then, computational modeling offers a more reliable solution.
Modeling a 3D Inductor in COMSOL Multiphysics
COMSOL Multiphysics provides all of the tools you need to fully characterize your inductor in the application for which it is being employed. The Modeling of a 3D Inductor tutorial model from the Application Gallery, which is also the introductory model for the AC/DC Module, provides a good illustration of some key features of the software. This takes the stress out of learning how to characterize and design inductors.
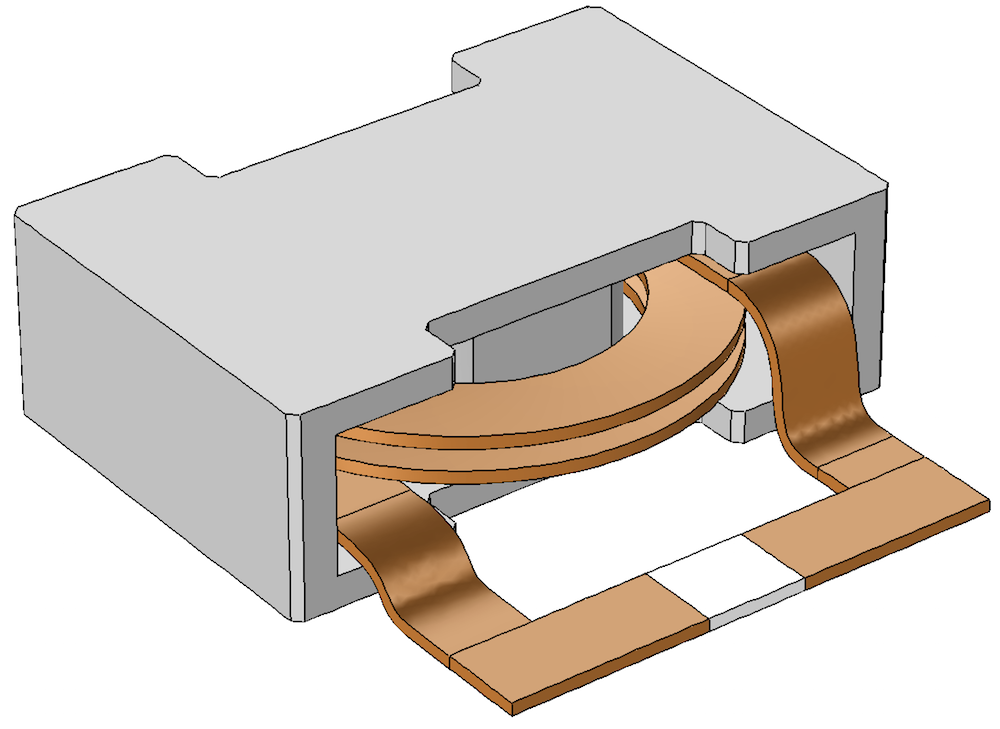
An inductor geometry for our finite element model.
In a real-world device, current may be driven through the inductor in various ways. A set voltage, current, or power can be applied. This could be a constant value, it may oscillate, or it may depend on time in a more complex way. In this application example, the Single Turn Coil feature and the Lumped Port feature (used at low and high frequencies, respectively) drive the conductors with a current, showing how you can drive your coils in a realistic way, no matter the application.
The steps for modeling your 3D inductor in COMSOL Multiphysics.
COMSOL Multiphysics not only allows easy set up of circuit models, which you can do within the software itself or by importing a SPICE net list, but also the subsequent connection of those circuit models to finite element models. You can connect your inductor to a driving circuit using the built-in connection features between the full 3D model of the inductor and the circuit model with minimal effort, since COMSOL Multiphysics detects which parts can be coupled together — and presents you with these options in a handy drop box.
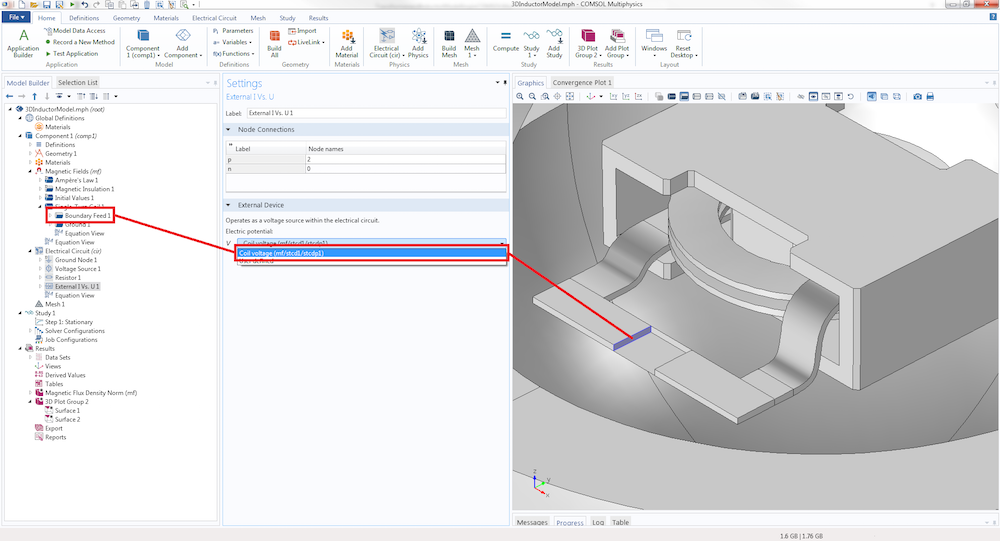
When you select the input feature from the drop box, the inductor’s terminal (highlighted in blue) is automatically coupled to the circuit model.
At high frequencies (at which your inductor might be operating), it is well known that the current in a conductor is confined close to its surface due to the skin effect. In the application example, this effect is included via the Impedance boundary condition in COMSOL Multiphysics. Resolving current flow in the thin layer is a computationally costly procedure, so simplifying it as a boundary condition saves you time and allows you to investigate your design more quickly.
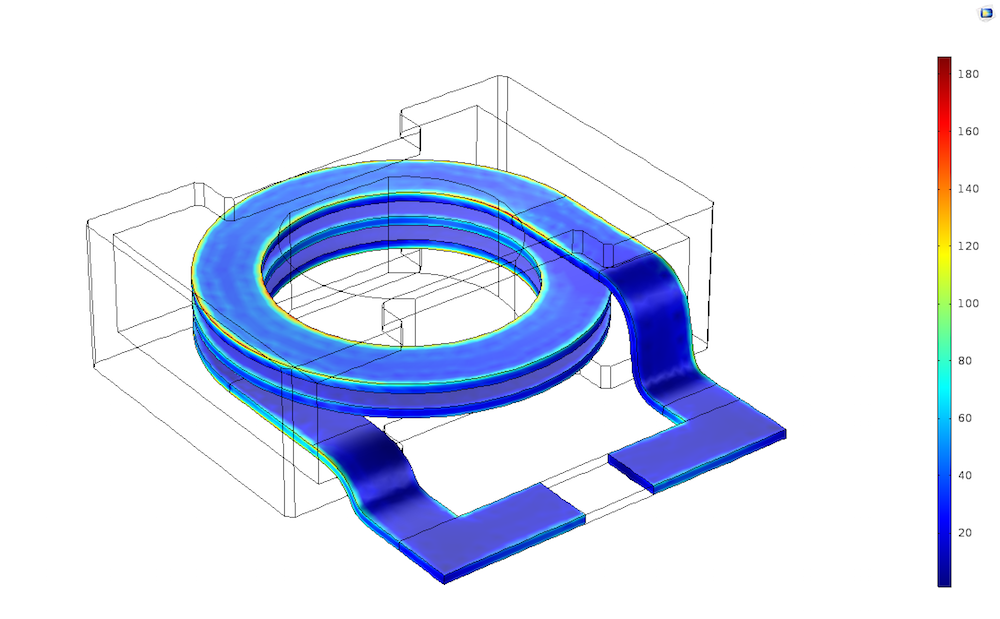
The currents (Am-2) generated on the surface of the coil at a high frequency. Note that the nonuniform nature of the current flow is fully captured.
The Q factor of the inductor itself crucially depends on material properties of its core, particularly the losses. The flexibility of COMSOL Multiphysics allows you to modify the properties of the material as needed in order to include these losses in your model. Any eddy current losses are automatically included in the calculation and here, the dielectric loss in the core is added to the model via a user-defined imaginary contribution to the dielectric constant, εr. Using the same simple approach, you can add magnetic losses to your model via the complex-valued magnetic permeability, μr.
Postprocess and Analyze the Results of Your Inductor Model
If you have management to win over or clients to impress, you can set up powerful plots of your results with just a few clicks using the built-in postprocessing capabilities of COMSOL Multiphysics. The software automatically calculates and provides access to the variables you evaluate to assess your inductor design, such as the magnetic field, currents, and rate of losses. The 3D inductor application example demonstrates how to set up the detailed image shown below.
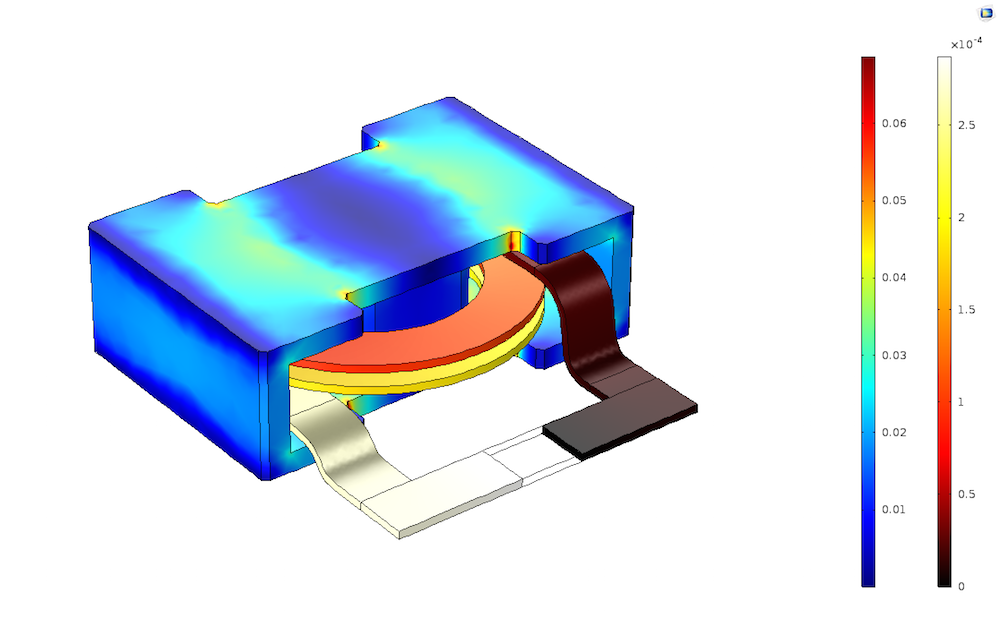
In the core, the magnetic flux density at the surface (T) is higher where the material is thinner, since it carries roughly constant flux. In the coil, a local potential is set up across the conductor (V).
With a little more time, you can extend your results to include some of the other plot types available, such as Streamline or Arrow plots.
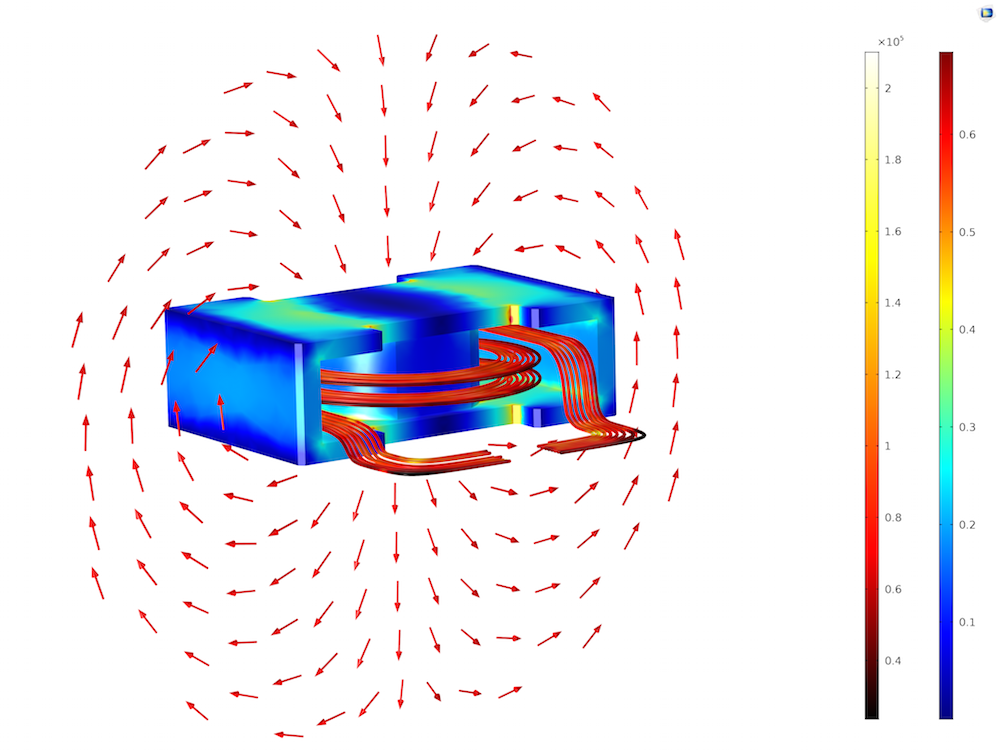
In the core, the magnetic flux density is shown at the surface (T). In the coil, streamlines of the current density (Am-2) show the higher current density inside the curved parts. The arrows in the surrounding areas show the magnetic field direction.
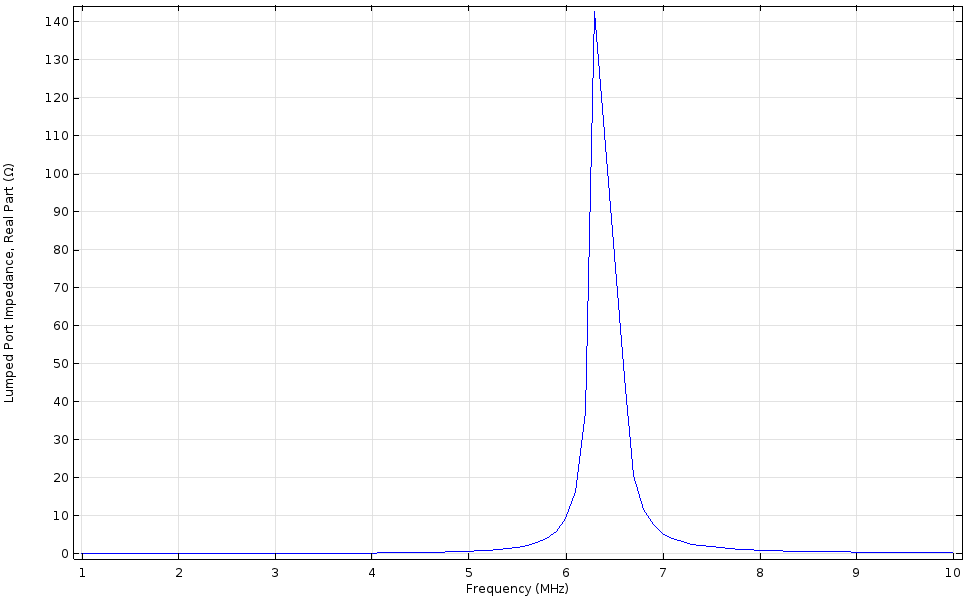
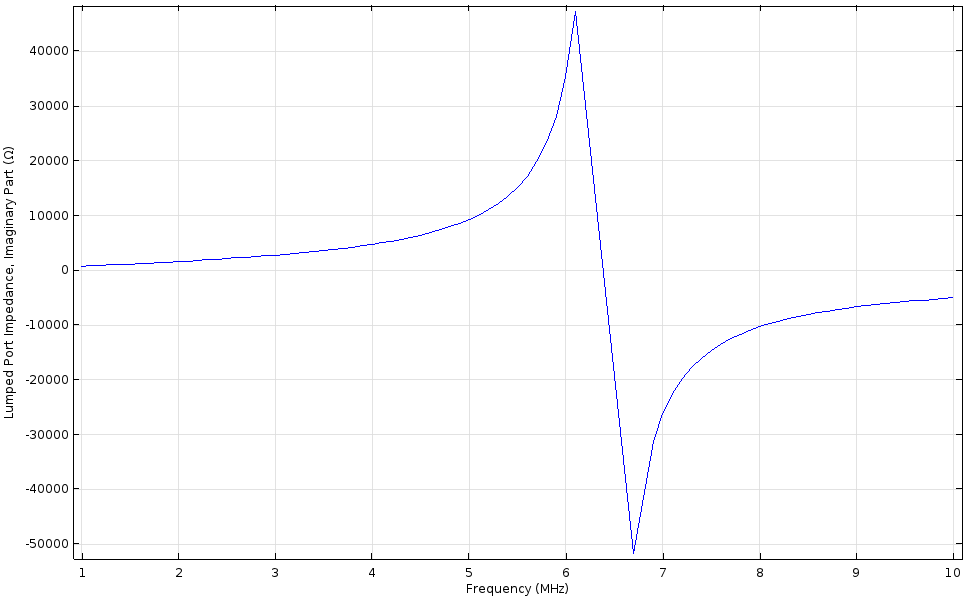
Finally, for the ultimate purpose of your model, you need the impedance values and resonance frequencies for your inductor. One of the many variables COMSOL Multiphysics automatically calculates is the exact impedance of the inductor at each frequency, so these parameters can be plotted with ease. Using the built-in real and imag operators, you can plot the real (resistive) and imaginary (inductive/capacitive) parts of the impedance, where the resonance can easily be seen.
The real (left) and imaginary (right) parts of the impedance, Z, showing the resonance and the switch between inductive and capacitive behavior.
In the imaginary part, you can also see that the sign changes from positive to negative when passing the resonance frequency, signifying that the device goes from acting primarily inductively to primarily capacitively at high frequencies, which is exactly as expected.
Expanding Your Inductor Model to Consider Thermal Effects
COMSOL Multiphysics is designed to easily integrate different physical effects in a model — this is the “multiphysics” aspect of the software. One way you can extend this inductor model is to consider its electromagnetic heating. The conduction currents in the coil, eddy currents, and dielectric/magnetic losses in the core all produce heat that spreads through the highly thermally conductive metal components and perhaps into the surrounding device and circuit board. Using the Induction Heating interface, you can easily add a calculation of the rate of heating and temperature distributions in your inductive device.
Learn More About Inductor Modeling in COMSOL Multiphysics
- Check out another inductor tutorial model in the Application Gallery:
- Learn about how others have applied COMSOL Multiphysics to their inductive device designs:




Comments (1)
Umid Jamolov
July 20, 2023This example uses a lumped port for electrical excitation, though user defined geometrical parameters do not represent the wire size. Could you, please, explain how geometry of the port was defined?