
If you’ve ever gone on a road trip, you know that it’s a bit of a pain — literally. Part of why your body aches after driving long distances is due to whole body vibration (WBV), which can cause fatigue; motion sickness; and, eventually, serious health problems. To design systems that reduce WBV for cars and other applications, engineers need an efficient way to visualize the effect of vibrations on the human body. That’s where simulation comes in.
Minimizing Not-So-Good Vibrations
WBV is any vibration that’s transferred to the human body. While studies over the years have investigated its potential benefits for physical therapy and fitness applications (like the one shown below), the negative side effects are a more pressing concern in other areas. Common symptoms of WBV include fatigue, back pain, and motion sickness, and extended exposure can result in digestive issues, vision and balance impairment, bone damage, and more. WBV can be felt when riding in vehicles or using power tools and heavy-duty equipment.

Vibrating belts (also called “jiggling machines”) supposedly harnessed WBV to burn fat circa 1950. Image by Andrew Kuchling. Licensed under CC BY 2.0, via Flickr Creative Commons.
To better protect against WBV, engineers can analyze the impact of vibrations at different frequencies on the human body. Since simulating the response of the entire body is computationally expensive, an alternative is simplifying the description of its behavior via a lumped model. To model multibody systems like this one, engineers can use the Multibody Dynamics Module, an add-on product to the Structural Mechanics Module and the COMSOL Multiphysics® software.
Lumped Modeling of the Human Body
The lumped model shown here is a spring-mass-damper model that consists of three main parts:
- Body
- Shoe
- Ground
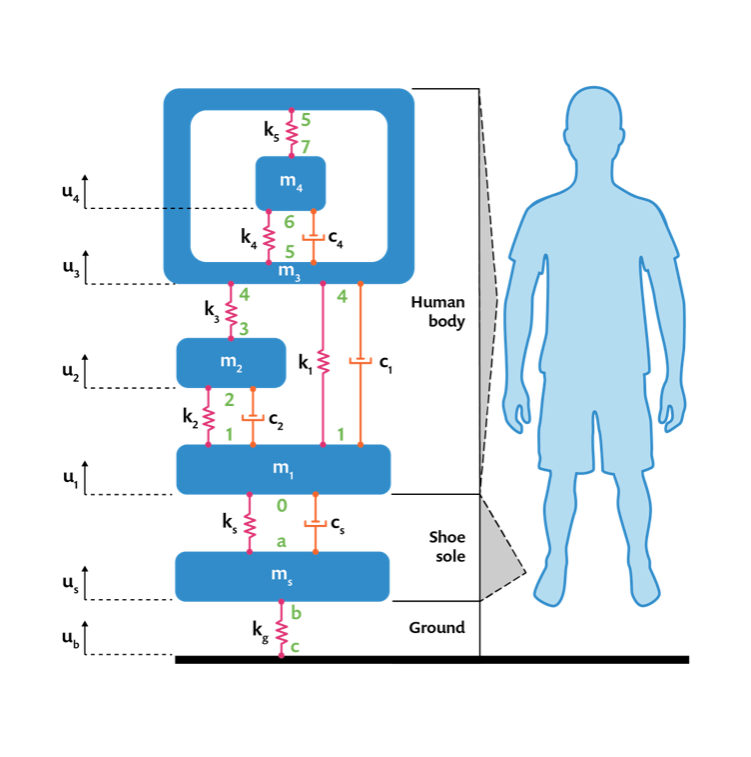
Lumped model of a human body, shoe, and the ground.
To model all three parts, you can use the Mass, Spring, and Damper nodes in the Lumped Mechanical System interface.
To represent the human body, one common model is the four-body model, which includes five springs, three dampers, and four masses. These masses each have their own degree of freedom (DOF) and are categorized as:
- Upper rigid
- Upper wobbling
- Lower rigid
- Lower wobbling
The shoe has one spring, damper, mass, and DOF. For simplicity’s sake, you can assume that the force between the shoe and foot is a linear function of spring deformation (rather than a more realistic nonlinear function).
The ground is modeled with a spring. To examine how ground stiffness affects the transfer vibration to the body, you can test different types of soils, such as soft (99 kN/m), hard (359 kN/m), and very hard (880 kN/m).
In order to solve the model, both eigenfrequency and frequency-response analyses are performed. The eigenfrequency study is fairly straightforward, calculating the first five natural frequencies of the model — one for each DOF. The frequency-response analysis computes the response of the body for a given base excitation applied at the ground, providing insight into factors like displacement and the force of the springs.
Evaluating the Frequency-Response Results
The results of the frequency-response study show how much the body and shoe move in response to the vibration at various frequencies. You can see that the amount of displacement depends both on the frequency as well as the location of the mass. For example, the upper rigid and wobbling masses are moved more than the lower masses at the first natural frequency, while the lower masses and the shoe have a relatively higher displacement amplitude at the second natural frequency.
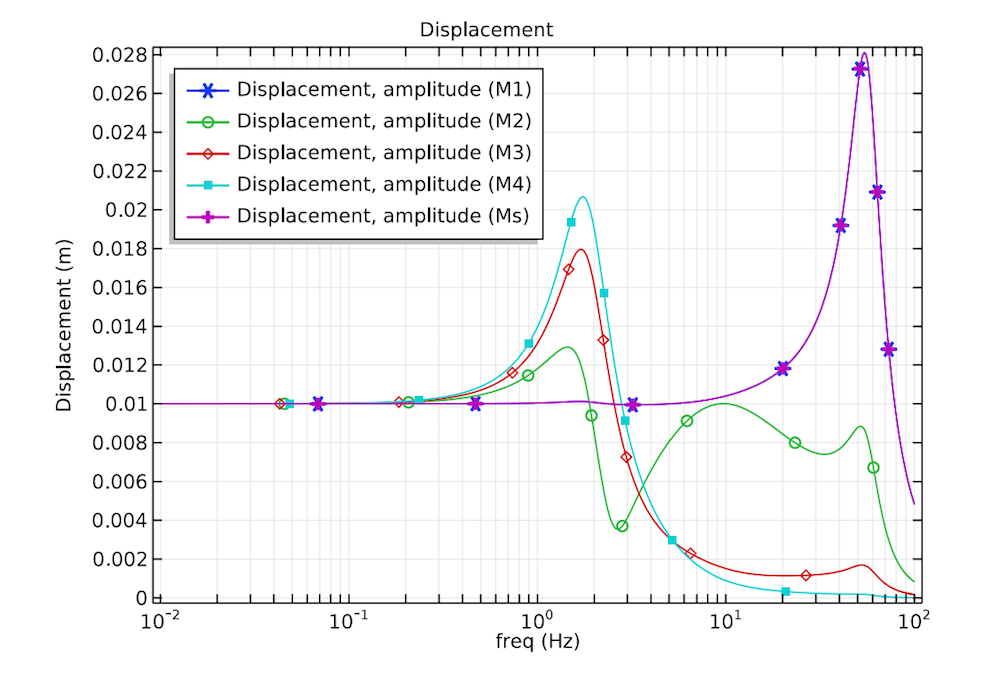
The displacement amplitude of the lower rigid mass (dark blue), lower wobbling mass (green), upper rigid mass (red), upper wobbling mass (light blue), and shoe (pink) for a range of frequencies.
It’s important to determine the forces in the springs, which get “stretched” and “compressed” by the vibrations. In an attempt to restore themselves to equilibrium, the springs exert a force on the connected masses, which can result in damage over time. Here, you can see that (in general) the higher the frequency, the more force the springs can generate.
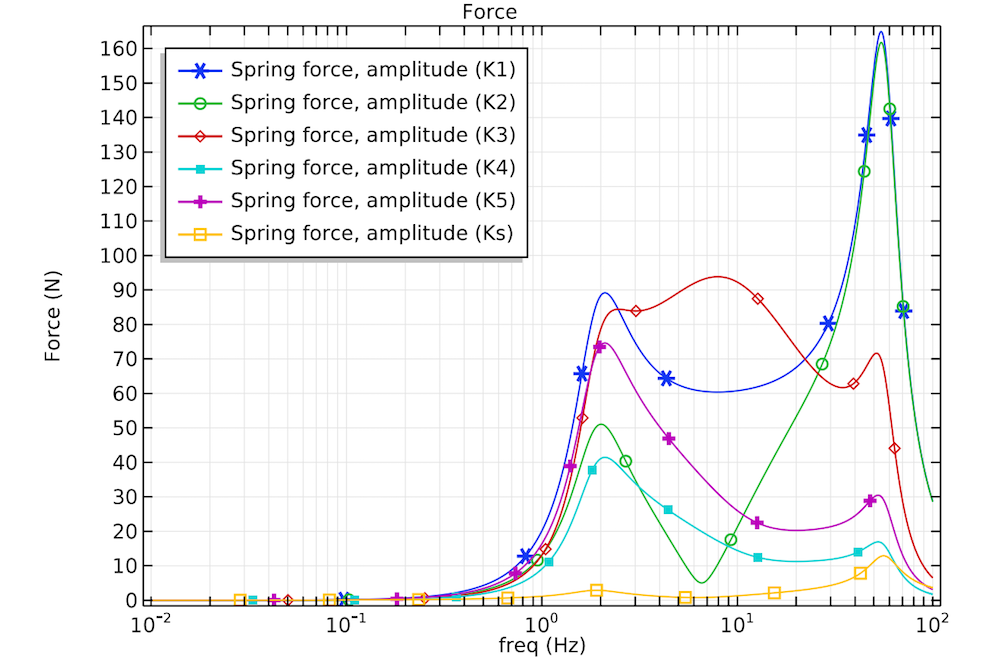
The spring forces in the body and shoe.
You can also examine how movement is transferred through the body, which is critical when trying to isolate the vibration. The results depict the vertical displacement transmissibility of the lower wobbling mass for the three kinds of soil stiffness. Near the first natural frequency, the transfer amount spikes at about the same time for all of the soils. However, as the frequency increases, the peak occurs later for the harder soils.
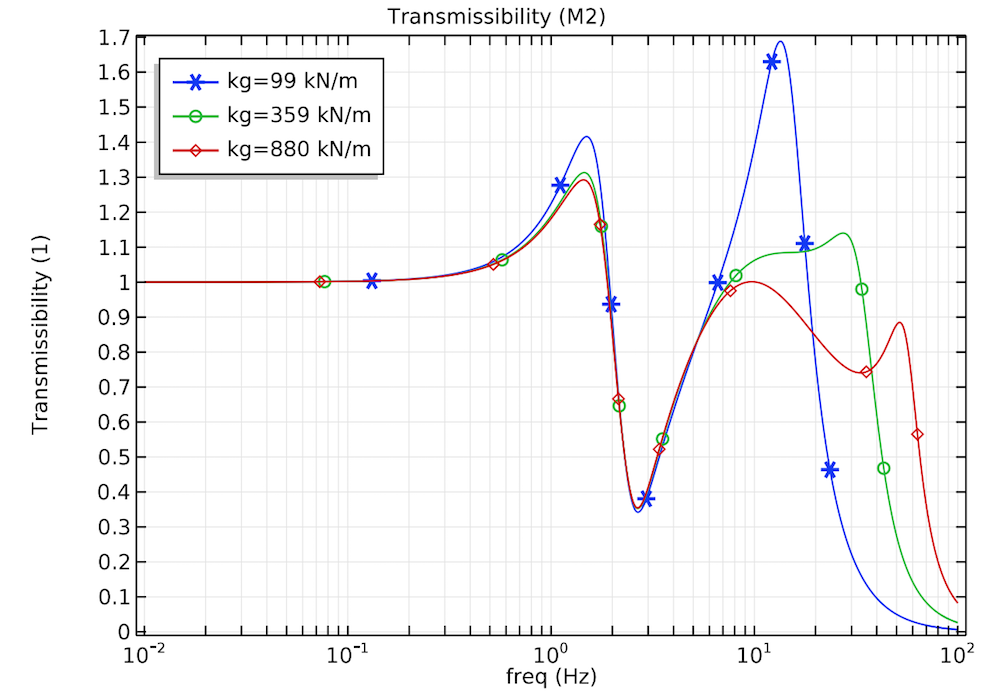
The vertical displacement transmissibility of the lower wobbling mass for soft soil (blue), hard soil (green), and very hard soil (red).
Using a model like this one, engineers can examine the effect of vibration at various frequencies on the human body and improve the design of various vibration isolation systems, such as seats and vehicle suspension systems.
Next Steps
Try the model by clicking the button below. You’ll be taken to the Application Gallery, where you can download the documentation and MPH file.
Learn more about biomechanical modeling:




Comments (1)
Pavan Kumar
September 2, 2020What is the source of the above lumped model ?I mean is there any research paper from which you have taken the values of the different masses and spring and damper parameters .If yes , can you provide the name of the research paper ? I want it for academic purposes .