
Have you ever wondered how tigers develop their stripes? Alan Turing’s theory of morphogenesis offers one possible explanation for this occurrence, suggesting that patterns, such as stripes, develop naturally from initially homogeneous states. Today, we’ll take a closer look at Turing’s theory and explore some modern research on this topic, including the modeling of branching morphogenesis in COMSOL Multiphysics.
From Computer Science to Morphogenesis: The Contributions of Alan Turing
When you hear the name Alan Turing, morphogenesis may not be the first thought that comes to mind. Turing, a famous British mathematician, is more widely recognized for his contributions to the fields of cryptology and computer science. During the Second World War, Turing helped break a complicated German cipher called the Enigma code — an achievement that has recently become more well-known due to it being featured in a movie.
Turing is also credited with creating an artificial intelligence test called the Turing test as well as the first formal computer algorithm concept. Such achievements have led many to consider him to be the father of artificial intelligence and theoretical computer science.

Alan Turing’s theory of morphogenesis offers a prediction behind the development of stripes on a tiger. Image by J. Patrick Fischer — Own work. Licensed under CC BY-SA 3.0, via Wikimedia Commons.
It wasn’t until later in his life that Turing entered into the realm of mathematical biology. In 1952, he published a paper on his theory of morphogenesis titled “The Chemical Basis of Morphogenesis”. Here, he used a mathematical modeling system to explain how nonuniformity, in the form of repeating patterns, can spring from a natural, homogeneous state. In simpler terms, Turing’s model suggests that such patterns result from the diffusion of two morphogens: an activator and an inhibitor.
To better understand his theory, we can look at the example of how stripes develop on a tiger. Turing’s theory predicts that morphogens produce patterns of chemically different cells by activating some cells and inhibiting others. In the case of a tiger, the activator creates the dark stripes and the inhibitor prevents the dark color in the area surrounding the stripes. This reaction diffuses across a tiger’s cells, generating a repetitive pattern of stripes.
Research Studies Support Turing’s Theory
Modern research continues to further validate Turing’s theory. For example, in a study from the Centre for Genomic Regulation, researchers found evidence that fingers and toes are patterned by a Turing mechanism. Such conclusions were drawn from computational predictions, with physical experiments confirming these findings. A team at King’s College London also produced experimental evidence validating Turing’s speculative theory. They identified specific morphogens used in Turing’s model and observed the effects predicted by this theory. Further experiments from researchers at Brandeis University and the University of Pittsburgh illustrated similar patterns arising from once identical structures.
The findings from these and other studies on Turing’s theory of morphogenesis can be applied to a range of applications, from biomedical uses to growing soft robots with specific patterns and shapes. In the next section, we’ll see how a team of researchers further investigated this theory with the help of COMSOL Multiphysics.
Analyzing Branching Morphogenesis with COMSOL Multiphysics
Modeling the complex biological processes in morphogenesis and organogenesis (the process where tissues develop into complex organs) can be difficult for two reasons: due to the parameterization of the computational models and the fact that it is not feasible to directly measure several of the parameters.
To account for such challenges, a team of researchers from ETH Zurich and the University of Nice-Sophia Antipolis turned to COMSOL Multiphysics. Using the simulation software, they looked to evaluate different methods for parameter optimization and explore the possibility of using experimental data as a means to quantitatively study, parameterize, and discretize computational models.
The first step was to create a Turing-type model based on receptor-ligand signaling. This model, as the group previously proposed, can be used to model branching morphogenesis in both the lungs and kidneys.
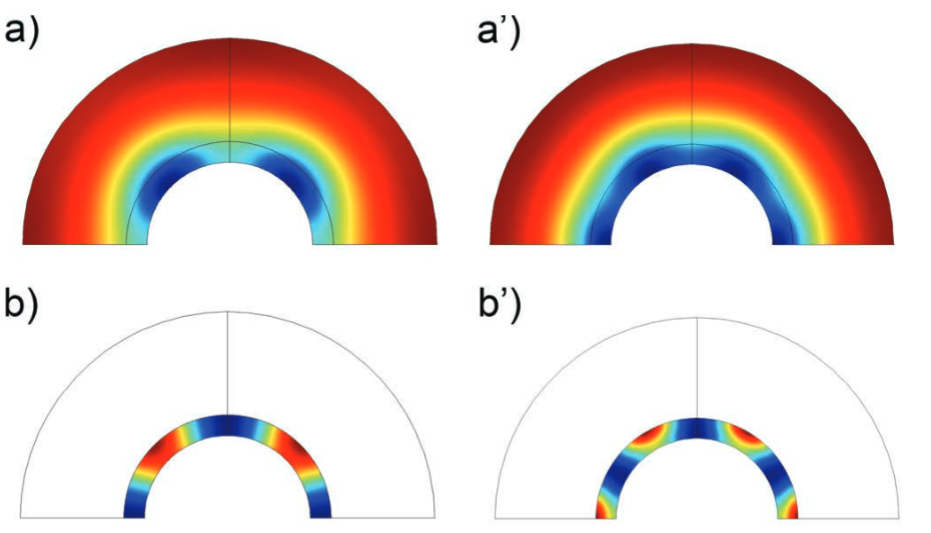
A simple Turing-type model. Images by D. Menshykau et al. and taken from their COMSOL Conference poster submission.
Two parameter optimization methods were tested with this model: a gradient-based optimization solver (SNOPT) and a gradient-free optimization solver (Coordinate Search).
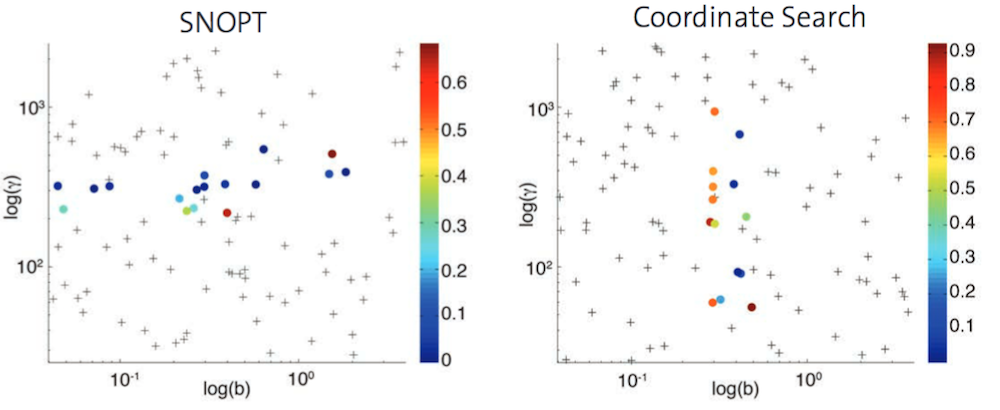
Convergence of the two optimization solvers. Points depict the initial values of the optimization solver that lead to convergence, while crosses depict a failure to converge. Different colors represent the value of the objective function when the optimization ends. Images by D. Menshykau et al. and taken from their COMSOL Conference poster submission.
The results from the study show that SNOPT and Coordinate Search share a drawback: For both of these methods, you can only recover the correct parameter values from a confined region of the parameter space. Therefore, the research team developed a three-step strategy to optimize the parameters of Turing-type models:
- Evenly sample the relevant parameter space
- Pick points that have minimal cost-function value
- Have the local optimization solver (SNOPT or Coordinate Search) use these points as a starting condition
Next, the researchers investigated the parameterization of image-based models, a common method for reproducing experimental data in simulations. 2D time-lapse movies of embryonic kidneys in vitro were used for the image-based model of branching morphogenesis. Through this approach, the researchers tested the ability of their mechanism to accurately predict growth areas throughout the process.
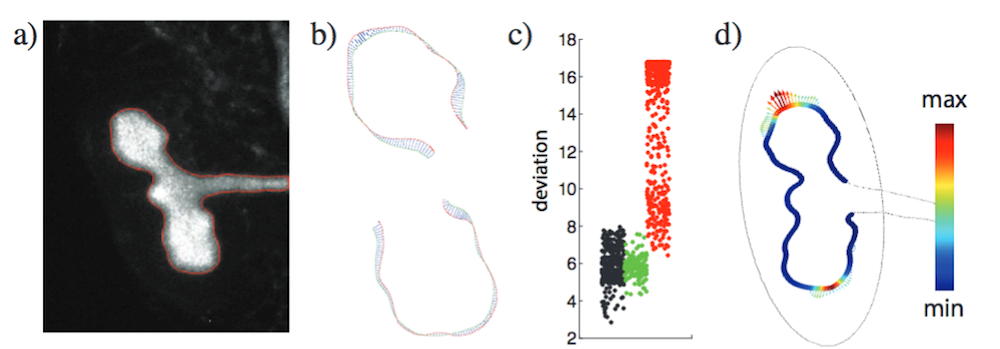
The process of image-based modeling. a) Time-lapse movie screenshot. b) Enlarged image of the kidney explant and calculated displacement field. c) Deviation for points in Turing space (black), in between (green), and outside the Turing space (red). (d) The growth field and the distribution of U2V (the ligand-receptor complex) on the epithelium-mesenchyme border. Images by D. Menshykau et al. and taken from their COMSOL Conference poster submission.
Findings showed that the Turing-type model adequately reproduced the observed growth areas of embryonic kidneys. As such, it was concluded that image-based data can be used when studying the mechanisms in charge of organ development and for solving, parameterizing, and discretizing models.
Simulation Studies Offer Further Insight into Turing’s Theory of Morphogenesis
Turing’s theory of morphogenesis is still evolving today, with researchers continuously finding new ways to model and utilize it. Simulation studies, such as those presented here, can help offer a better understanding of the mechanisms controlling morphogenesis while furthering the design of computational models for studying morphogenesis and organogenesis.
Along with the studies highlighted today, researchers at ETH Zurich and the University of Nice-Sophia Antipolis have used COMSOL Multiphysics to perform additional analyses pertaining to organogenesis. One study, for instance, helped address the fact that cell boundaries, and possibly subcellular compartmentalization, can greatly affect signaling networks during organogenesis. In a more recent study, researchers explored techniques for image-based modeling using the example of limb bud development. You can learn all about these studies and more in the section below.
Further Resources on Using Simulation to Better Understand Natural Phenomena
- Read the full paper: “Simulating Organogenesis in COMSOL Multiphysics®: Parameter Optimization for PDE-based Models“
- Explore additional research on organogenesis:
- Browse other blog posts relating to simulation’s role in analyzing natural phenomena:



Comments (0)