It’s quite common to use focused laser light to rapidly heat materials for various purposes, including within the semiconductor processing industry. Here, we will look at a Gaussian profile laser beam with periodically pulsed intensity, heating up two different semitransparent materials deposited onto a silicon substrate. To model this, we will solve a multiphysics modeling problem using the temperature field and the Beer–Lambert law. Let’s further explore the model and see how to set it up…
A Gaussian Profile Laser Beam Illuminates a Silicon Wafer
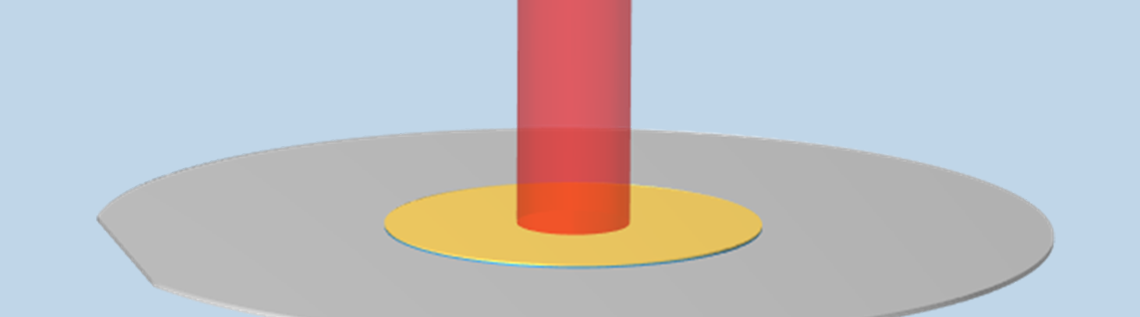
We will use an example of a two-inch diameter silicon wafer (illustrated below) that has two different materials at the center, each 100 μm thick and with a 1 cm radius. The wafer is illuminated from the top by a Gaussian profile laser heat source that is rapidly pulsed in time. These materials are both semitransparent at the laser wavelength of 700 nm, but are opaque to longer-wavelength, infrared radiation. The silicon substrate is doped and highly absorptive at all wavelengths.
![]()
A pulsed laser illuminates two layers of semitransparent material on an opaque wafer.
Since all materials have planar boundaries that are normal to the incident beam, all of the incident light will be propagating in a uniform direction parallel to the incident beam. There will be reflection at the interface between the materials, but no refraction or diffraction. The thickness of both layers is much greater than the wavelength, so we can assume that the coherence length is much smaller than the layer thickness. We can solve this problem using the Beer–Lambert law, which describes the attenuation of light in a semitransparent medium. This equation is solved using the Radiative Beam in Absorbing Media interface within the COMSOL Multiphysics® software. However, since there is reflection, there are some nuances that we will need to look into carefully.
Understanding the Physics and Setting Up the Model
Since the deposited layers are circular, and since the laser is focused onto the center, we can ignore the wafer flat and treat the model as being entirely axisymmetric. This enables us to reduce the model to the 2D axisymmetric modeling plane. In this plane, we simply draw three rectangles defining the wafer and the two deposited layers, and assign different material properties to all three. With that, the geometry and the materials are defined, and we can focus on the physics.
Let’s start by following the beam path through free space, from the laser source above the wafer downward, along the z-axis. We will say that we have a 40 W, 700 nm-wavelength laser, and that the beam has a Gaussian profile with a standard deviation of 1.5 mm. The laser is on for 75 ms and then off for 25 ms, or the laser uses pulsed heating with a 75 percent duty cycle and 100 ms period. This type of stepped loading in time is addressed via the Events interface, which is used to introduce a Discrete State variable, ONOFF, that is either 0 or 1 in time.
We will not explicitly model the laser source nor the beam path through free space; we will only model the light interacting with the materials. At the boundary to the top layer, the material with a refractive index of n_{top}=2.4, there will be some reflection due the difference in refractive indices, as given by the Fresnel equations:
Although this equation holds for complex-valued refractive indices, it’s reasonable to consider only the real-valued component of refractive index in our evaluations, since the imaginary component of the refractive index is quite small. Under the additional assumption that there is not any absorption at the interface (such as due to a very thin coating of absorptive material), the transmittance is T=1-R. This completes the information that we need to set up the Incident Intensity feature of the Radiative Beam in Absorbing Media interface, as shown in the screenshot below.
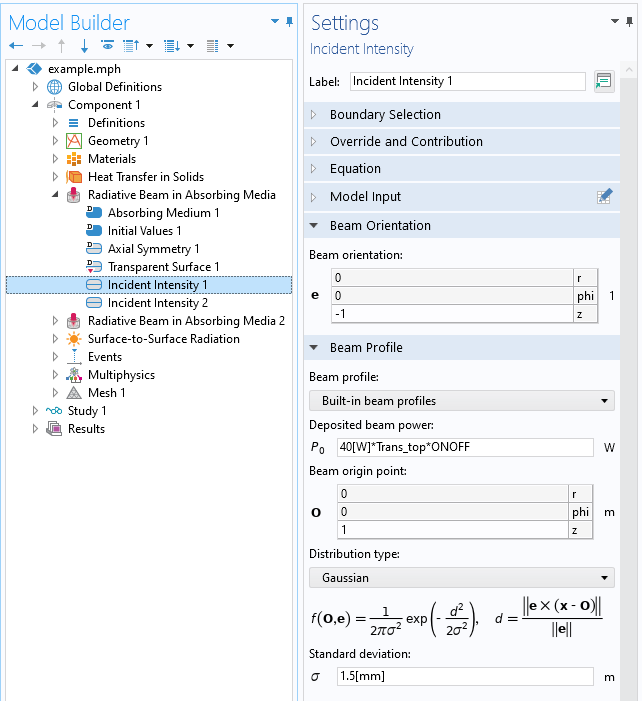
The settings for the Incident Intensity feature.
As the beam traverses through the first layer of material, its intensity decreases in proportion to the absorption coefficient, \kappa, which is determined from the equation:
where k is the imaginary component of the refractive index, and \lambda_0 is the free-space laser wavelength. The absorption coefficient can be temperature dependent, but we will start with it being a constant. Given the intensity distribution of the beam profile across the top surface, the beam intensity is computed throughout the domain.
At the dielectric interface between the top and bottom layer of deposited materials, there will again be reflection and transmission described by the Fresnel equations. The reflected component of the beam is handled with the existing Radiative Beam in Absorbing Media interface, simply by adding a second Incident Intensity feature. It’s possible to add any number of Incident Intensity features to this interface; each will introduce an additional variable to solve for, and these variables will be named rbam.I1, rbam.I2, …, and so on. In this second Incident Intensity feature, we can introduce a user-defined beam profile that is based on the first beam intensity and the Fresnel reflection coefficient. By changing the sign of the beam orientation, the partial reflection of light at this interface is fully accounted for, as shown in the screenshot below. Theoretically, there will be an additional reflection of this beam at the top boundary, but this second reflection is sufficiently small, so we will ignore it.
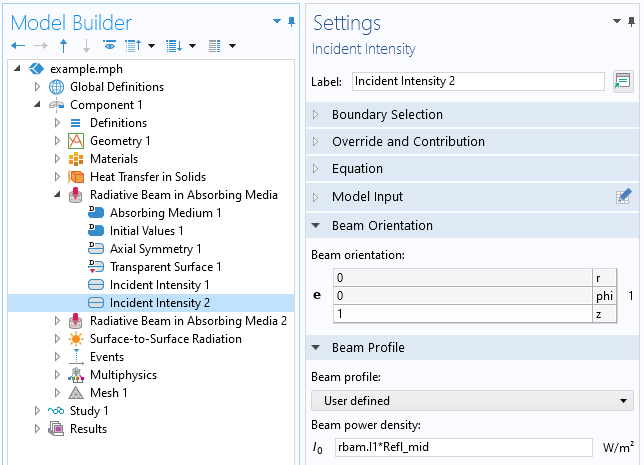
Screenshot of the second Incident Intensity feature, accounting for reflection at the dielectric interface.
Next, we follow the beam as it traverses across the dielectric interface into the second layer of semitransparent material. Since there is a change in the intensity of light across this boundary, we have to add a second Radiative Beam in Absorbing Media interface and define the incident intensity based on the Fresnel transmittance and the first beam from the first Radiative Beam in Absorbing Media interface.
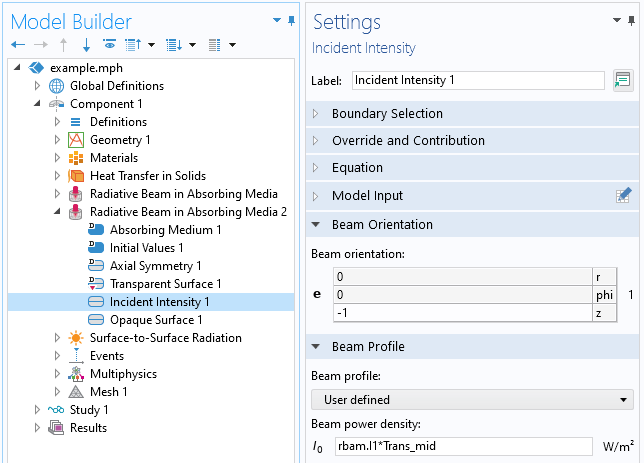
Screenshot of the Incident Intensity feature of the second radiative beam in the Radiative Beam in Absorbing Media interface, used for the intensity in the bottom domain.
Finally, let’s address what happens as the light reaches the bottom of the second layer, and hits the silicon wafer substrate. We will assume that the silicon wafer is doped so that it’s highly absorptive and nonreflective. Since all light reaching this boundary will be absorbed over a sufficiently small distance, we can say the light is absorbed at the boundary. For this situation, the Opaque Surface boundary condition will deposit all of the energy at the selected boundary, and this completes the modeling of the laser light as it propagates through the structure. With this combination of features, we have completely modeled the incident laser beam as it traverses through our model. We can now turn our attention to the thermal model.
Modeling the Change in Temperature Over Time
The wafer is initially at a uniform temperature of 300 K. There is conductive heat transfer through all domains, and we will assume that there is no significant thermal resistance at the interfaces between the materials, that is, there is no temperature difference across the material interfaces, and flux is continuous. This situation is the default assumption of the software, but if we did wish to override it, we could add a Thin Layer or Thermal Contact feature.
At 100 μm, the layers are thick enough that the classical Fourier’s law for heat transfer applies, although it’s worth mentioning that heat transfer at the nanoscale is an active area of research amongst COMSOL users; see, for example, our guest blog post “Hydrodynamic Thermal Transport in the Kinetic-Collective Model”.
As for a thermal boundary condition, we will assume that the wafer is on a perfectly insulating base, and sitting within a near-vacuum process chamber. This means that there will be no conductive or convective heat transfer cooling, but there will be radiative heat transfer to the chamber walls that are assumed to be held at 300 K. We will further assume that the wafer temperature will only rise a few hundred degrees Kelvin, and thus the radiative emission will be in a longer-wavelength band, as compared to the incident laser. The implication of this is that we can, conceptually speaking, use a two-band model for the radiative heat transfer. The incident radiation from the laser is already completely handled via the Radiative Beam in Absorbing Media interfaces. The emitted radiation in the longer-wavelength band (due to the rise in temperature of the wafer relative to the process chamber walls) can be modeled with a single-band Surface-to-Surface Radiation interface, coupled with the Heat Transfer in Solids interface. The Surface-to-Surface Radiation interface computes the view factors between all of the exposed surfaces and to the ambient space.
It’s worth mentioning that, in this case, there is only surface-to-surface radiation near the small inside corner where the layers protrude above the wafer; everywhere else has a view factor of unity to ambient. If we wanted to make a slight simplification, we could omit the Surface-to-Surface Radiation interface and instead use the Surface-to-Ambient Radiation boundary condition within the Heat Transfer in Solids interface. There is negligible difference in computation time and in the results, so here we use the more accurate approach of computing view factors using the Surface-to-Surface Radiation interface.
We will also need to pay careful attention to the meshing of this device. The Radiative Beam in Absorbing Media interfaces solve a first-order partial differential equation and use, by default, a linear discretization of the fields. Based on the absorption coefficients, we know that the intensity will change significantly through the thickness of the two layers. We also know that the intensity variation of the laser beam profile over the surface is quite gradual. This justifies a mapped mesh within the layers, with high-aspect-ratio rectangular elements. Of course, we will always want to investigate mesh and solver relative tolerance refinement as we progress in our modeling complexity, as discussed in our previous blog post “Intro to Modeling Transient Heating of Solids in COMSOL Multiphysics®”.
With the setup complete, we will solve this problem using the time-dependent solver and save data at steps taken by the solver. We can then plot out the temperature profile and the absorbed heat, as well as the temperature at the upper-middle point over time, as illustrated below.
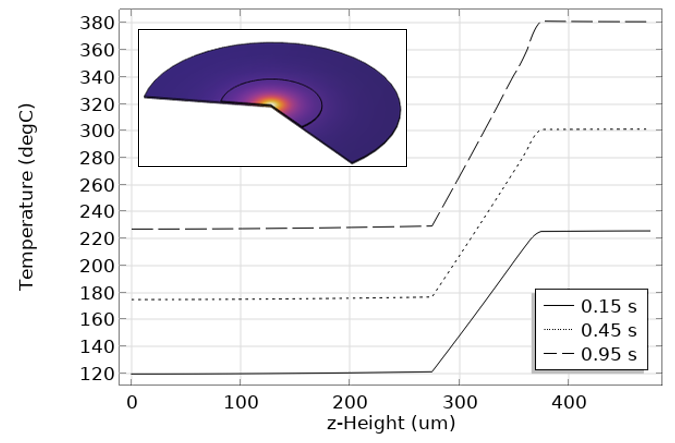
The results of the z-height versus temperature.
Finally, we will introduce a material nonlinearity by making the absorption coefficient of the bottom layer go up with increasing temperature, for illustrative purposes. The comparison between the absorption coefficients of the two semitransparent materials is shown in the plot below. With the nonlinear absorption coefficient, there is greater heating of the material as the temperature rises. Due to this material nonlinearity, we also need to refine the mesh in the layer with nonlinear properties.
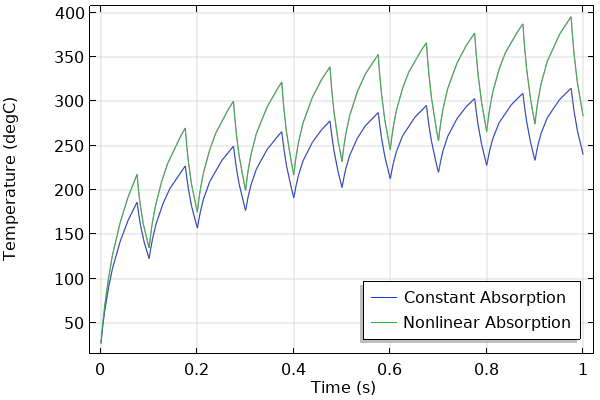
Comparing temperature over time using two different material models.
Closing Remarks
We have introduced a modeling approach for addressing the heating of a semitransparent material. The collimated radiative heat source, the laser, is modeled using a set of Radiative Beam in Absorbing Media interfaces, which handle the semitransparent nature of the material at the laser wavelength as well as the reflections at dielectric interfaces. The pulsed heat source is handled via the Events interface, and the longer-wavelength infrared reradiation is handled via the Surface-to-Surface Radiation interface. This modeling approach is applicable to the semiconductor processing field or any situation where collimated light is incident on semitransparent materials.
If you’re interested in these types of simulations, please feel free to download the example model discussed here by clicking the button below:







Comments (16)
Olesya Nakonechna
January 9, 2023Thank you very much for very interesting and useful blog!
Walter Frei
January 9, 2023 COMSOL EmployeeThank you Olesya!
Giacomo Zanellati
January 11, 2023Can this model be applied if the laser beam is not perfectly parallel to the surface? If not, does a possible solution exist?
Walter Frei
January 11, 2023 COMSOL EmployeeHello Giacomo,
Yes, as long as the boundary is parallel, you will simply also need to apply Snell’s law as well as the Fresnel equation. In each domain, the direction of propagation would be different, but nothing else would change. On the other hand, focusing or divergence of the beam, due to curved surfaces or varying refractive index, is not addressed by the Beer-Lambert law equation. In that situation, one would need to use the Beam Envelopes method in the Wave Optics Module.
Joseph Zarrabi
January 20, 2023I think it will be great if this model is provided with older version of COMSOL 6.0
with a detail instructions how to setup the model using the COMSOL usual pdf file.
Cheikh Samba SARR
February 3, 2023Hello Frey,
I would like to ask you a question for clarification, I ask a lot and I also follow COMSOL webinars on heat transfer but I don’t have an answer yet that helps me for my simulation.
I study heat transfer on components that have been subjected to localized radiation from a homogeneous beam laser.
My Beam size can be rectangular or square depending on the area where you want to heat and the focal length is at a distance X from the stage.
I know where to apply my boundary conditions to the boundary but the concern is expressing my average laser power density in the homogeneous distribution.
Is it possible that you give me suggestions and an explanation on this subject?
Komal Chaudhary
March 18, 2024Hi Walter Frei,
I am trying to buildup a model where we have two thin metal layers deposited on a silicon substrate and we heat them up with a laser beam. I am using the module ‘Radiative beam in absorbing media’ to see the laser intensity distribution inside the system like you did it in this example. The top layer in my system has high absorbing coefficient and the laser intensity should not reach to the second layer. When I put my parameters in your model, it is working fine as it is expected to be. But in my model, I see that two separate decaying intensity distributions in each layer. Can you help me with this?
Komal Chaudhary
March 18, 2024Hi Walter,
I am building a model where we have two thin metal layers deposited on a silicon substrate and we heat them up with a laser beam. I am using radiative beam in absorbing media module to see the intensity distribution in the system like you did it in this example. It is kind of similar model but in cartesian coordinates. The top layer in my model has very high absorbing coefficient and the laser intensity should not reach to the second layer. When I put my parameters in your model, it is working fine as it is expected to be. But in my model I get two separate exponentially decaying intensity distributions in each layer. Can you please help me with this? Thank you.
Walter Frei
March 18, 2024 COMSOL EmployeeHello Komal,
This sounds exactly as expected. Note that if you have specific questions about your particular model, you should contact COMSOL Support.
Melika Afshar
May 14, 2024Hi,
I we heat he material with fs laser beam, in order to calculate the intensity we should consider nonlinear absorption.
Can you please tell me how we ca set about environment to be in a liquid and so we have convection and cooling during laser heating.
Walter Frei
May 15, 2024 COMSOL EmployeeHello Melika,
Note that there are multiple ways of modeling convection: https://www.comsol.com/blogs/modeling-natural-and-forced-convection-in-comsol-multiphysics/
The modeling approach can be highly unique to the case that you are working on, as it does sound like you’re working on something slightly out of the ordinary.
Mirza Sahaluddin
September 25, 2024Hi Walter,
Thank you very much for very this truly useful blog. I would greatly appreciate it if you could explain more about what exactly are the variables “rbam.I1” and “rbam.I2”. I would greatly appreciate any details on this or any helpful references.
Thank you!
Walter Frei
September 26, 2024 COMSOL EmployeeHello Mirza,
Yes, these are internal variables for the first and second beam intensities. In general, with regards to understanding internal variables, see:
https://www.comsol.com/support/learning-center/article/Viewing-and-Accessing-the-Equations-and-Variables-for-Physics-Feature-Nodes-30761/122
Mirza Sahaluddin
September 26, 2024Hi Walter,
Thank you very much for your prompt reply and the very helpful link. I have two questions that I would greatly appreciate your input on:
1) Does rbam.I1 encompass all the rbam.ii1.xxx variables in the incident intensity 1 (e.g., rbam.ii1.P0, rbam.ii1.er, rbam.ii1.ephi, etc.)?
2) In this context, should rbam.I1 be understood as the intensity of the laser beam at any given point within the entire domain of the top layer? If so, does it represent the beam intensity reaching the top-middle layer interface, which is then partially reflected according to the Fresnel reflection coefficient
3) Thus, if the boundary condition was supposed to be reflection instead of opaque at the bottom of the second layer when the beam hits the silicon wafer substrate, would this be applied as rbam2.I1*Reflection?
Thank you again
Shojaa Abusakha
August 28, 2025can this model work for picosecond laser?
Walter Frei
August 29, 2025 COMSOL EmployeeHello Shojaa,
At 1ps, the maximum distance that a photon travels is ~0.3mm, so the assumption of a uniform intensity beam does indeed start to become quite questionable, yes, if dealing with materials of comparable length-scales. Furthermore, at those time-scales one may also need to question if Fourier’s Law heat transfer is appropriate to use. It is definitely an interesting research question.