
An interesting question came up the other day that I felt would make an excellent blog post since it allows us to discuss one of the very powerful, and often underutilized, features of COMSOL Multiphysics: the Global Equation. In this post, we will look at using global equations to introduce an additional degree of freedom to a model. This additional degree of freedom will represent something we do not want to model explicitly.
The Scenario
Let us consider a small house with a person inside, as shown below. There is a fan circulating air, mixing it thoroughly, so we can assume the inside air temperature is constant. There’s a stiff breeze outside, and we know the outside air temperature. We’ll also assume that the ground underneath is at a constant temperature. The average person at rest dissipates about 75 W of heat. We would like to find out the air temperature inside of the house, and the temperature gradient through the walls.
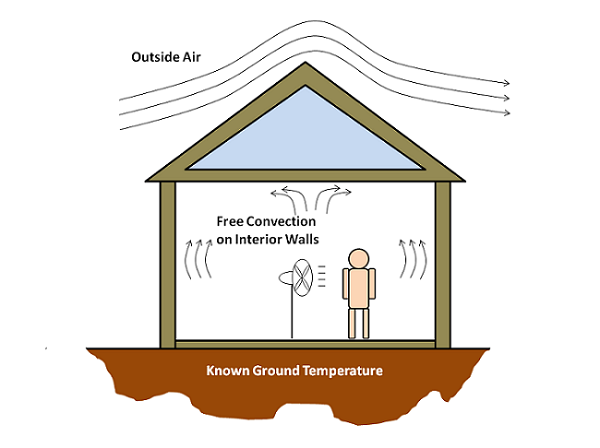
Setting up the Model
Now, if we wanted to be very accurate, we could build a conjugate heat transfer model of this, and solve for the temperature field and the fluid flow inside of and around the house. (If you want to build a model of all the airflow in your room, please see this example of Displacement Ventilation in a Room to get started.)
However, solving for the fluid flow is going to be computationally demanding, as compared to just solving a heat transfer problem. And if you’re familiar with heat transfer modeling, you know that there are tabulated heat transfer coefficients, h, for vertical and horizontal walls that relate the inward heat flux, q'', to the wall temperature, T, and the air temperature, T_{air} via the equation: q''=h(T_{air}-T). If the air is hotter than the wall, heat will flow into the wall and vice versa. So using this equation, we don’t need to solve for fluid flow at all, but we do need to know the air temperature inside the house. Let’s draw a simplified engineering sketch of how this can be modeled:
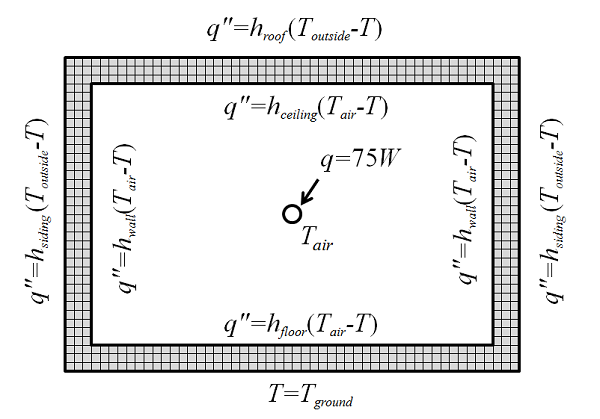
Here, the house walls are modeled explicitly via the finite element method; the true wall dimensions are used and appropriate material properties are applied. The field being solved for is the temperature of the walls and we are assuming steady state conditions. We know the outside temperature, ground temperature, and all heat transfer coefficients, so this problem is almost solvable. But… we do not know the air temperature inside the room, T_{air}. So the air temperature is the one additional unknown that we need to add to this finite element model.
Along with the unknown, we need to know what equation this variable must satisfy. In this case, the choice is clear: we want to ensure that the sum of all the heat going in and out of the volume of air equals zero. That is, if we take a surface integral of the heat flux between the interior walls and air, and add the heat contribution from the person, this should equal zero:
Using Global Equations to Solve the Model
Let’s take a look at the Global Equation interface, which gives us a list of variable names to enter — we’ll use Tair — and the equation to satisfy. In the field defining the equation, we will use an Integration Coupling Operator named intop to integrate the normal total energy heat flux variable, ht.nteflux, across all of the wall boundaries. Since this is a steady state problem, it doesn’t matter what initial conditions we give for this variable. When setting this up, make sure to turn on the Advanced Physics Options in the Model Builder so that you can add global equations to a physics interface. When you are solving a problem with global equations, you will want to use a Fully Coupled Stationary Solver with a Direct Linear System Solver.
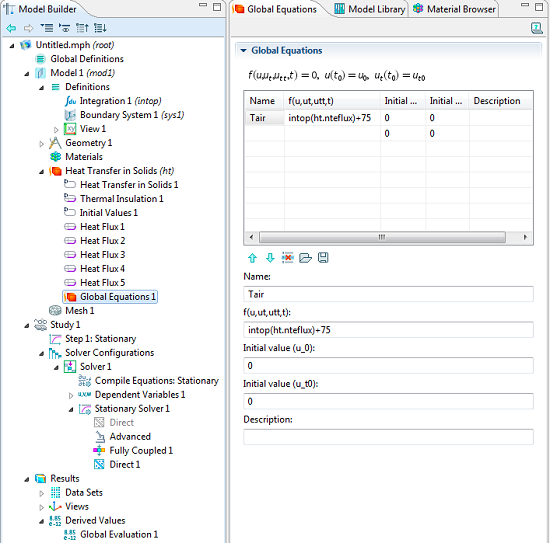
The Global Equation interface, as well as the appropriate solver settings.
After we solve this model, we’ll be able to visualize the temperature distribution on all of the interior walls, and evaluate the air temperature via Results > Derived Values > Global Evaluation. We have simplified the problem by assuming that the air has a uniform temperature, and thus simplified the modeling, via the usage of the Global Equation. The approach shown here assumes that the thermal mass of the air is negligible, but if we wanted to model this as a transient problem, we could include the time-derivative of the air temperature and the total mass and specific heat of air in the global equation as well.
Next Steps
If you would like to see an example that walks through all of the steps of setting up a global equation in your model, please see this example of Using Global Equations to Satisfy Constraints. If you think that using global equations will be helpful for your modeling and are interested in learning more about COMSOL Multiphysics, please contact us.




Comments (6)
Ishant Jain
September 21, 2013Please share some documentation, how we can use equation directly.
Enzo Maier
January 5, 2014Dear Walter,
great information you provide in this blog! Although I still have a question on “.., you will want to use a Fully Coupled Stationary Solver with a Direct Linear System Solver”. Why is that? If I add a Gloal Equation as separate physic, can I use a segregated stationary solver / iterative linear solver? Thanks for your reply.
Walter Frei
January 6, 2014 COMSOL EmployeeDear Enzo,
The reason why you would want to use a fully coupled solver are described here:
http://www.comsol.com/blogs/solving-multiphysics-problems/
Basically, you cannot solve one equation without the other. If you try to solve it by hand, the issue will become immediately apparent.
YongweiLi YongweiL
December 11, 2014Dear Walter:
Interior wall Overrided by Thermal Insulation is not applicable In Comsol 4.4 ,How did you implement Boundary Selection of Heat Flux ?
Walter Frei
December 22, 2014 COMSOL EmployeeDear YongweiL, There is no interior wall with a thermal insulation to override here. The boundaries conditions you are applying here are not *interior* to the modeling domain.
Modess Seyednezhad
June 25, 2018Hi,
I am amature in using COMSOL. I have couple of questions:
1. How can I combine a TEC app to the other components of a model. The same as what is done in the video: https://www.comsol.com/video/simulate-thermoelectric-devices-tecs
2. Is there any way to use an app for a 2D model ?
3. In case of using several TEC module for cooling a surface, the modules are electrically in series ?
4. How can I define a TEC app for a heat sink or a hot surface?
5. How can I use TMY3 temperature data instead of ASHRAE ? (How can I import a table into COMSOL)