
Meshing a geometry is an essential part of the simulation process, and can be crucial for obtaining the best results in the fastest manner. However, no one wants to be bogged down figuring out the exact specifications for their mesh. To help combat this problem, COMSOL Multiphysics has nine built-in size parameter sets when meshing. Here, we’ll discuss size parameters for free tetrahedral meshing. Swept meshing with prismatic and hex elements, and other types, will be covered in future postings.
Introducing the Size Parameters
The built-in parameter sets range from Extremely fine to Extremely coarse with Normal sitting right in the middle. These parameter sets are determined for each geometry based on rules that are hard-coded into the COMSOL software for ease-of-use, and tested by us to produce high-quality meshes for most geometries and applications. Of course, as with everything in COMSOL Multiphysics, the parameters comprising the predefined sets can be modified when limited computer resources, the complexity of the geometry, or the physics application calls for it.
Let’s take a look at the different size parameters and how to modify them for our specific needs, using a one-quarter piece of an engine piston as our geometry.
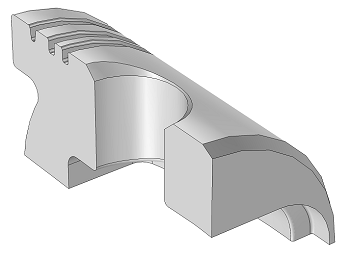
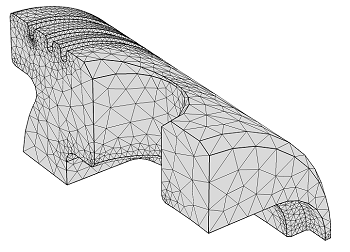
A one-quarter section of a piston geometry (left) and the same geometry after adding a Normal predefined mesh in COMSOL Multiphysics (right).
Working with Mesh Parameters
When creating a model in COMSOL Multiphysics, the mesh always defaults to a Physics-controlled mesh with a Normal element size. We can easily use this, or any of the other predefined parameter sets, as a starting point when modifying individual parameters. The predefined element sizes are simply sets of parameters, five parameters to be exact, that are available for modification:
- Maximum element size — limits how big each mesh element can be (lower value => finer mesh)
- Minimum element size — limits how small each mesh element can be (lower value => finer mesh)
- Maximum element growth rate — limits the size difference of two adjacent mesh elements (lower value => finer mesh)
- Curvature factor — limits how big a mesh element can be along a curved boundary (lower value => finer mesh)
- Resolution of narrow regions — controls the number of layers of mesh elements in narrow regions (higher value => finer mesh)
Adjusting one or more of these parameters lets you build a custom mesh, specific to your needs. In the case of the above geometry, the Normal element size parameter set is satisfactory for the bulk of the geometry, but results in too large elements for the fillets and the bevel around the hole.
Let’s also assume that a Finer mesh is too computationally taxing. Therefore, starting from a Normal mesh, we modify a few of the parameters. Lowering the Minimum element size and Curvature factor, and raising the Resolution of narrow regions, allows for a better resolution of the fillets and the bevel around the hole. We can also increase the Maximum element growth rate to allow for larger elements in the bulk of the component.
But after all these changes how do we know that the quality of the mesh is still good enough for our needs?
Comparing Mesh Statistics
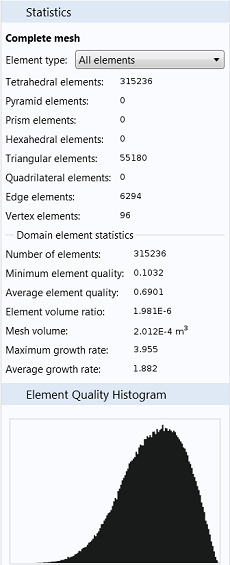
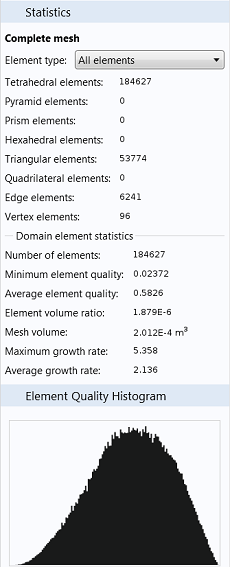
After building a mesh, right-clicking on the Mesh 1 node and choosing Statistics brings up a detailed report of the mesh elements (three of which are shown below). While there are different applications that require different mesh qualities, the Minimum element quality statistic is a telling one. Usually, a value greater than 0.1 is all we need.
As you can see in the three images below, both the left and center mesh meet these requirements, while the right-most mesh does not. The left image is a Finer mesh; the center image is a Normal mesh with a custom Minimum element size, Curvature factor, and Resolution of narrow regions; and the right image is a mesh that is the same as the center mesh, but with a higher Maximum element growth rate added.
Depending on your model and computational limits, the center mesh would be a good choice that balances element quality and number of elements, while having an adequate resolution of the geometry.
A Finer mesh that is computationally taxing (left), a custom mesh with satisfactory quality (center), and a custom mesh with element quality that could be too low (right).
Further Reading
- The model you see here can be found in our Model Gallery
- To learn more about meshing in COMSOL Multiphysics, check out these related blog posts by my colleague Walter:








Comments (3)
Oscar Diaz
November 13, 2014Dear Andrew,
Thanks for your interesting blog entrance, has been of a great help. Right now I’m struggling a lot with a simple stationary 3D electrostatics model that I have to run within an iterative loop commanded from Matlab. The problem that always kills my simulation after a few hours is the mesh creating point while the program has advanced a few steps.
After trying several different techniques, I came to realize that the detail I am using for certain edges is affecting drastically the way the free-tets are created next to this ‘detail’ edges or boundaries.
Could you tell us your experience while using free-tets meshing in combination with certain edge or free-triangular elements in a 3D meshing?
Andrew Griesmer
November 13, 2014 COMSOL EmployeeHi Oscar,
Thanks for commenting, I am glad this blog post has been helpful. For an answer to this specific question, submitting a support case is your best option: http://www.comsol.com/support.
Daniel Cavan
May 12, 2020Hi Andrew,
The value of 0.1 for the minimum element quality statistic, is that based on anything?